基于不等式约束的顾及长度变形的坐标系统转换方法

陶叶青，杨 娟

(宿州学院地球科学与工程学院，安徽宿州234000)

一、引 言

GPS的定位成果是基于WGS-84参考框架的，因此利用GPS技术建立或改善国家和地方坐标系的控制网需要将其定位成果转换至国家或地方坐标系中。我国现行的参心坐标系统的点坐标是用二维或平面坐标与高程分开表示的，因而无法精确地用空间三维直角坐标表示出其点位坐标。因此，为实现GPS控制测量成果的坐标系统转换，需将GPS定位成果的控制点间的空间三维坐标差(基线向量)表示为二维或平面坐标，这不可避免地会引起一定的长度变形，而相关的测量规范规定其变形值不应大于1/40 000［1］。为了减小由控制点间的空间距离转换为平面距离过程中引起的长度变形，人们提出更改中央子午线或建立区域性椭球的方法［2-4］。应用这样的方法所建立的坐标系更改了原有国家坐标系的基本投影与参考椭球的属性，虽然减小了长度变形，但在GPS坐标系统转换过程中，其最终转换成果已不是国家或地方坐标系，且区域性椭球的算法不易于实现。此外，传统的由数学转换模型实现坐标系统转换的方法并没有顾及长度变形这一因素。

为将GPS控制测量的成果转换至国家或地方坐标系中并顾及长度变形因素，拟将不等式约束应用至坐标系统转换中。不等式约束问题的研究可追溯至40多年前，文献［5］首先研究不等式约束的回归分析;文献［6-8］将不等式约束引入大地测量领域，并在变形检验、GPS数据处理、大地控制网的优化等方向取得了一定的应用成果;文献［9-10］对不等约束的具体解法进行了研究;文献［11］提出应用最优化计算理论中的罚函数方法实现不等式约束的平差算法。针对坐标系统转换过程中不可避免地会出现长度变形的问题，应用不等式约束将长度变形量纳入坐标系统转换模型，进行平差处理。根据文献［11］提出的不等式约束的平差算法，实现了能够顾及长度变形的坐标系统转换。

二、转换方法与模型

坐标系统转换常用的有七参数与四参数模型，以平面坐标系统转换为例，通常采用的转换模型为［12］

式中，a、b为两个平移参数;α为旋转参数;λ为尺度比参数;(x0，y0)、(x，y)为控制点在原坐标系(WGS-84坐标系)与目标坐标系中(国家坐标系)的平面坐标。应用GPS建立控制网进行坐标系统转换时，若要获得式(1)中控制点在原坐标系中的平面坐标，就需要将GPS的空间三维直角坐标转换成大地坐标，并将大地坐标按高斯-克吕格投影至平面坐标。这一过程有两个长度变形：①将空间三维直角坐标转换成大地坐标，相应的空间距离转换成椭球面大地线距离的长度变形;②将大地坐标转换成平面坐标，相应的椭球面大地线距离转换成平面距离的长度变形。长度变形对坐标系统的转换有显著的影响，但式(1)并不能够顾及这方面的影响。

式(1)可表示成以(x，y)目标坐标为变量的函数模型

不等式约束的模型可表示为

式中，x表示目标坐标(x，y);B为转换模型参数;l为原坐标(x0，y0)。

不等式约束的主要对象是控制点在实现坐标系统转换后，对用平面坐标表示的长度变形量进行约束。相关规范一般要求根据控制点平面坐标反算距离与测距仪复测距离相对变形值小于1/40 000［1］。据此，约束不等式具体的形式为

式中，D为测距仪实测精度;(x1，y1)、(x2，y2)为目标坐标系中控制点的平面坐标。假设

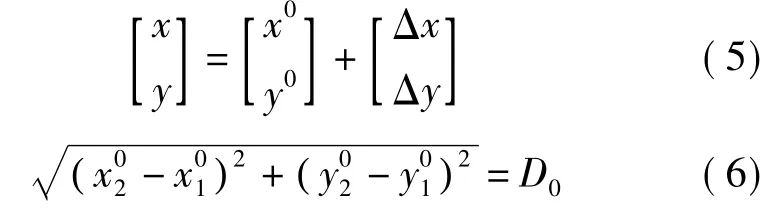
式中，(x0，y0)为控制点在目标坐标系中的初始转换值;(Δx，Δy)为其改正值;D0为根据初始值反算的初始距离。将控制点平面坐标表示的反算距离线性化为

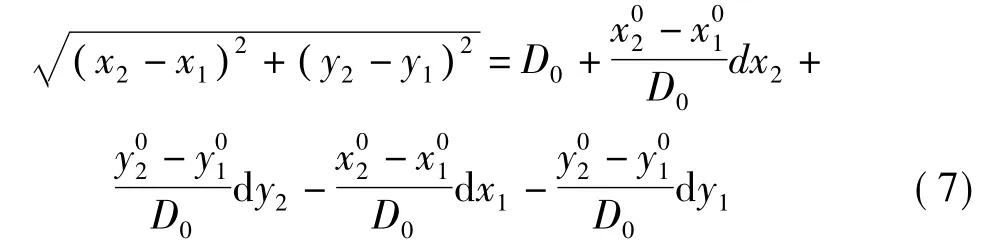
因此，式(4)可表示为

式(8)为式(3)中二式的具体形式。不等式约束模型(式(3))可通过优化计算中的罚函数方法转化为无约束最优化问题［11］

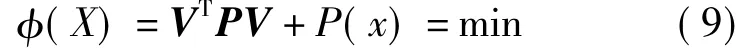
式中，VTPV=(Bx－l)TP(Bx－l)=min;P(x)为罚函数，它要求当参数x满足式(3)中二式时，P(x)值取为零，不等式约束转化为普通的最小二乘平差。当参数x不满足式(3)中二式时，不等式约束转化为等式约束进行计算。此时

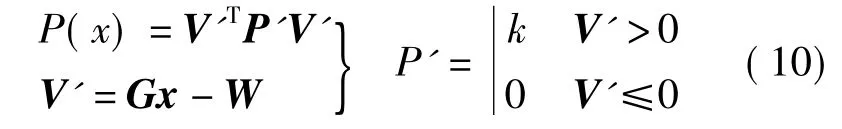
式中，k值根据经验取一正整数值。应用不等式对坐标转换过程中引起的长度变形进行约束的基本方法为：

1)首先应用一定的数学转换模型(式(1))进行坐标系统转换。

2)按国家相关测量规范的要求对控制点间的距离实测。

3)将控制点坐标与实测距离代入式(4)，如果满足条件，则应用其控制成果。

4)如果不满足条件，则使用式(9)重新进行平差计算。其中，罚函数的形式可通过式(10)确定，权值P'则根据控制点间的距离确定，进行迭代计算，直到都满足式(4)为止。

三、算例分析

结合应用式(1)实现GPS控制测量成果坐标系统转换的某线路工程控制点平面坐标，应用测距精度为±(2 mm+2×10－6×D)的TOPCON330全站仪对控制点间的距离进行实测，控制测量结果与实测距离、反算距离列于表1(部分数据选自文献［13］)，长度变形值 λ1列于表2。其中，λ1表明测距边2—3、3—4、4—5的长度变形值超出测量规范的要求，值大于1/40 000。因为1—2的长度变形值小于1/40 000，因此应用不等式对长度变形进行约束平差，结合式(9)与不等式约束实现的方法，只对控制点3、4、5坐标进行重新平差(1、2点坐标保持不变)，并进行迭代计算，控制点坐标与长度变形值λ2列于表2。λ2表明经不等式约束平差，测距边2—3、3—4、4—5的长度变形值符合测量规范的要求，值小于1/40 000。

四、结束语

本文根据不等式约束的基本思想，给出能够顾及长度变形的坐标系统转换模型与转换方法，给出对长度变形量约束的不等式具体形式，并对具体的转换步骤进行探讨。结合实测数据，对转换方法进行验证，结果表明这一方法能够在坐标系统转换过程中减小长度变形，使测量成果符合国家测量规范的要求。

表1 控制点坐标与点间距离 m

表2 不等式约束平差结果

［1］中华人民共和国交通部.JTJ/T 066—98公路全球定位系统(GPS)测量规范［S］.北京：人民交通出版社，1998.

［2］覃辉.某城市独立坐标系与1954北京坐标系转换方案［J］.测绘学院学报，2002，19(4)：247-250，254.

［3］冯亚明.利用GPS建立地方独立坐标系［J］.武汉城市建设学院学报，1996，13(4)：17-20.

［4］施一民，李健.地方独立坐标系的性质与区域性椭球的确定［J］.测绘通报，2001(9)：4-5.

［5］JUDGE G G，TAKAYAMA T.Inequality Restrictions in Regression Analysis［J］.Journal of the American Statistical Association，1966，61(313)：166-181.

［6］SCHAFFRIN B.Ausgleichung mit Bedingungs-ungleichungen ［J］.AVN，1981(6)：227-238.

［7］KOCH K R，RIESMEIER K.Bayesian Inference for the Derivation of Less Sensitive Hypothesis Tests［J］.Journal of Geodesy，1985，59(2)：167-179.

［8］REMONDI B W.Real-time Centimeter-accuracy GPS：Initializing While in Motion(Warm Start Versus Cold Start)［J］.Navigation，1993，40(2)：199-208.

［9］冯光财，朱建军，陈正阳，等.基于有效约束的附不等式约束平差的一种新算法［J］.测绘学报，2007，36(2)：119-123.

［10］宋迎春，左廷英，朱建军.带有线性不等式约束平差模型的算法研究［J］.测绘学报，2008，37(4)：433-437.

［11］朱建军，谢建.附不等式约束平差的一种简单迭代算法［J］.测绘学报，2011，40(2)：209-212.

［12］姚宜斌.平面坐标系统相互转换的一种简便算法［J］.测绘与信息工程，2001(1)：1-3，18.

［13］林晏.大型线路工程独立坐标系的建立方法研究［D］.阜新：辽宁工程技术大学，2010.