基于二次曝光法的切趾2 mm 短栅距光纤布拉格光栅制作研究

武洪波，陈爽，赵印明，陈喜

(中航工业北京长城计量测试技术研究所，北京100095)

0 引言

光纤布拉格光栅(FBG)作为敏感元件，在光纤传感领域有着很高的应用价值，一般采用裸光栅或封装后的光纤光栅传感器作为测试手段，光栅栅长即为测试点的尺寸，光栅长度越小测试点越精确。在航空领域，有很多毫米级小尺寸部位的结构健康监测，以及光栅内埋的复合材料损伤识别，都需要进行精确点监测。一般认为栅距在1 ～5 mm 的光栅即为超短栅距型，由于2 mm 栅距光栅的光谱性能在短栅距光栅中有一定的代表性，因此选取其作为研究对象。

光栅的反射谱中存在较多的旁瓣，其存在将反射无用波段的光波，从而影响整个光栅的性能。为减少旁瓣，可采用切趾［1－3］(Apodizing)方法，即在光栅的光致折射率变化中引入和光栅长度有关的函数包络，包络选取得当可以大幅提升光栅的边模抑制比。而切趾型短栅距光栅相较于普通长度切趾光栅，在反射率较高时带宽上涨迅速，反射率、3 dB 带宽和边模抑制比三项指标很难同时满足要求［4］，因此2 mm 光栅在切趾时需考虑不同的函数型及参数控制的影响，以使光栅的综合性能达到一个较为理想的状态。

1 理论模型

均匀光纤光栅的折射率调制幅度沿光纤轴向呈矩形分布，相应反射谱中反射主峰两侧有很丰富的边模。如果改变光栅折射率调制幅度的分布，使之符合某种钟形函数包络的形式，这就是所谓光纤光栅的切趾。切趾光栅反射谱谐振波长的右侧旁瓣得到抑制，但在短波长处却留有很明显的振荡。这种振荡的产生源于光栅的非均匀直流折射率变化，需要对进行了一次切趾的布拉格光栅进行直流分量切趾(二次曝光)［5－8］，引入一个直流修正项Δneff(z)，以改善光栅的性能。二次曝光切趾的光纤布拉格光栅的折射率分布表达式为

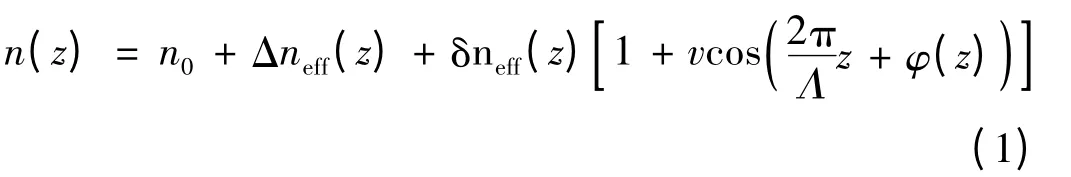
式中:n0为光纤纤芯折射率值;z 表示光栅长度范围;L 为光栅长度;φ(z)描述光栅啁啾，此处为0;δneff(z)为有切趾包络的交流平均折射率调制量;v 为折射率调制变化的条纹可见度;Λ 为平均光栅周期。式中引入直流平均折射率调制量Δneff(z)，其变化周期远大于光栅的折射率交流调制周期，意义是对光栅区域增加随z 变化的折射率背景补偿。而δneff(z)决定了干涉条纹的深度以及变化方式。引入直流调制项的耦合模方程为

式中:A+(z)与B+(z)分别为正向和反向传输模的振幅缓变包络;ξ+为光栅直流自耦合系数;κgac为光栅交流耦合系数。

对于非均匀光栅，利用耦合模理论求解析解极其困难，而传输矩阵法［1］(TMM)在这种情况是一种理想的求解方法。传输矩阵法将折射率非均匀变化的光栅均匀分为m 段，将每一段都用一个2 ×2 矩阵描述，然后将所有的矩阵相乘得到一个总的2 ×2 矩阵表示总光栅。m 一般取值为50 ～100 即可满足精度要求。设穿过第k 段后的电场幅度为A+k和B+k，光栅初始边界条件Am+= A+(L/2)=1，B0+= B+(L/2)=0，可以求得最终反射矩阵单元幅值A+m= A+(－L/2)与B+0= B+(－ L/2)。设第k 均匀段传输矩阵为Tk，可得到经过第k 段幅值传输等式为

传输矩阵Tk的表达式为

式中:dz=L/m，表示第k 均匀段的长度;κ 为第k 段的耦合系数;Ω 定义为

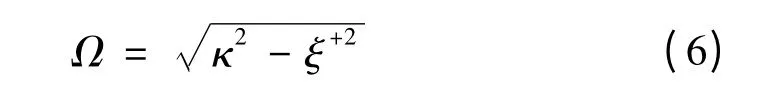
则可以得出总矩阵表达式为

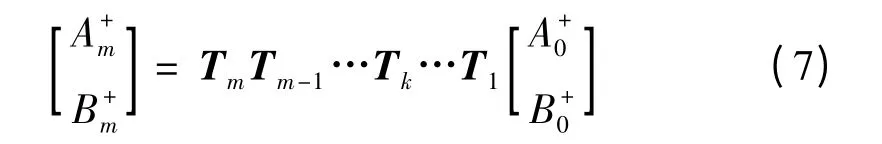
可得反射系数ρ 表达式为

2 数值仿真结果及分析

由于切趾实际上减弱了栅区边缘的条纹强度，相当于缩减了光栅有效栅长，光栅反射率上涨所需曝光量需进一步加大，光栅带宽会进一步增大，不利于传感解调应用。因此在进行切趾2 mm 光栅仿真时应权衡切趾强度参数取值，在有一定取舍的情况下达到光栅性能的最优化。调查行业内光栅要性能求，传感用2 mm光栅性能指标要求为反射率＞50%，半波全宽FWHM ＜1.5 nm，边模抑制比＞15 dB，由于光栅成品较仿真会有性能下降，在仿真时应调节参数，在满足带宽指标的情况下尽量提升边模抑制比。仿真时光栅设计中心波长λB=1550 mm，栅长L =2 mm，控制折射率调制量将光栅的反射率维持在85%附近，在同反射率条件下考察切趾效果。以均匀2 mm 光栅作为参考基准，反射谱如图1 所示。

图1 均匀2 mm 光栅反射谱

切趾2 mm 光栅仿真使用的切趾函数为3 种常用钟形包络函数，分别为:

1)Gauss 函数:

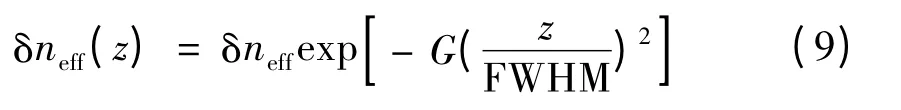
2)Tanh 函数:

3)Cauchy 函数:

函数式中z 取值为［－L/2，L/2］，为栅长范围;FWHM 指函数包络的半波全宽，一般取为栅长L 时效果较好。3 种切趾函数均有各自的切趾强度控制参数，控制着函数包络的形状，一般来说增大切趾强度可以提升光栅的边模抑制比，但同时伴随着带宽的上涨。切趾强度控制参数并不是越大越好，在大于某一阈值后性能提升有限。经过取值试验后，确定各切趾函数最佳取值组合如下:Gauss 型，G =8;Tanh 型，α =0.6，β=2.7;Cauchy 型，C=0。

最优切趾参数下，在Matlab 软件中进行了二次曝光切趾2 mm 光栅反射光谱仿真，光栅反射率均保持在85%附近，得到的反射光谱如图2 ～4 所示。所得到各项光栅性能参数仿真结果对比如表1 所示。

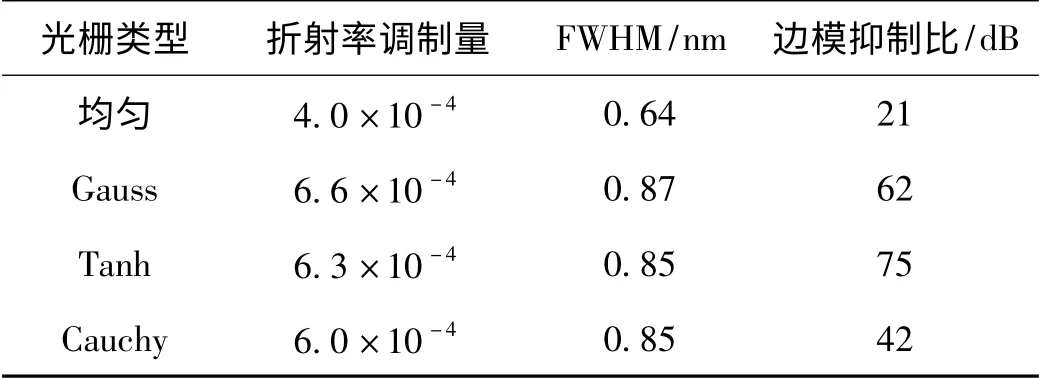
表1 二次曝光切趾2 mm 光栅性能参数对比

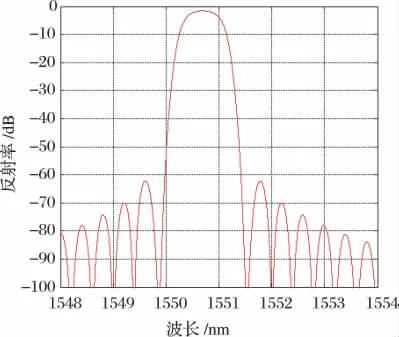
图2 Gauss 型2 mm 光栅反射谱

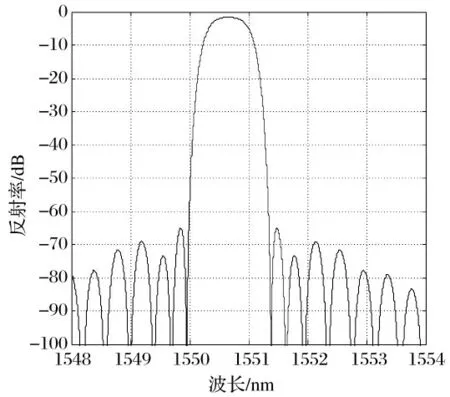
图3 Tanh 型2 mm 光栅反射谱

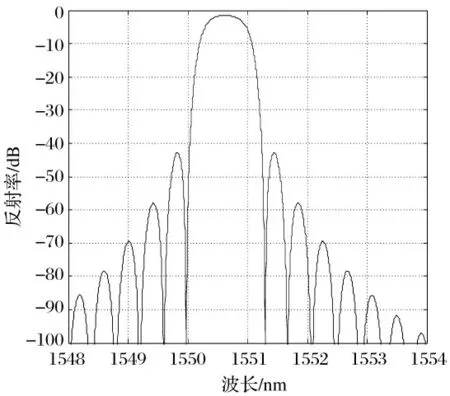
图4 Cauchy 型2 mm 光栅反射谱

从表1 的数据可以看出，同反射率下，二次曝光切趾光栅的边模抑制比较均匀光栅均有大幅度提升。Tanh 型、Gauss 型效果较好，边模抑制比较均匀光栅提升40 ～50 dB，改善幅度较大;Cauchy 型效果略差，较均匀光栅提升20 dB。切趾光栅的边模抑制比提升是以牺牲带宽为代价的，若切趾强度太大FWHM 很容易上涨超出指标，在所选用参数下FWHM 增长幅度在0.2 ～0.3 nm，均匀光栅的带宽为最小。二次曝光切趾光栅反射主峰两侧陡峭，图形理想。切趾光栅较均匀光栅所需折射率调制量上涨2 ×10－4～3 ×10－4，相应成栅曝光时间增长，需要更加严格的刻制环境条件控制。仿真结果看来，三种切趾型2 mm 光栅的性能均可满足目标性能需求。

3 实验验证

光栅刻制实验是在基于相位模板法和准分子激光的曝光系统下完成的，切趾函数的控制参数选取为仿真得到的最佳值，光栅刻制时在光谱仪中实时监测光谱变化，光栅反射率达到85%时停止刻制。二次曝光切趾是通过特殊设计的光学遮蔽板来实现的，通过改变遮蔽板上函数孔形状实现不同切趾函数配置，将通过遮蔽板的激光光束再经凸面镜聚焦到光纤纤芯上进行曝光写入。以Gauss 型遮蔽板为例，如图5 所示，上方函数孔用来曝光形成光栅结构，下方孔用来进行栅区折射率背景补偿。

图5 Gauss 型切趾遮蔽板

实验得到的均匀光栅以及3 种切趾型光栅的反射光谱如图6 ～9 所示。

图6 均匀2 mm 光栅反射谱

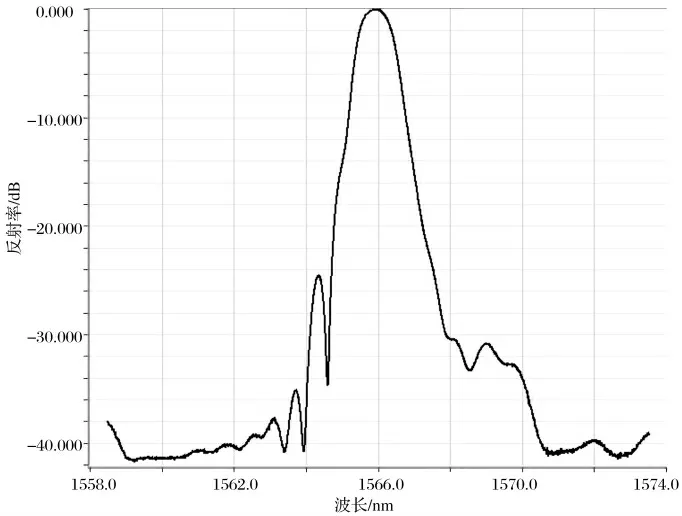
图7 Gauss 型2 mm 光栅反射谱

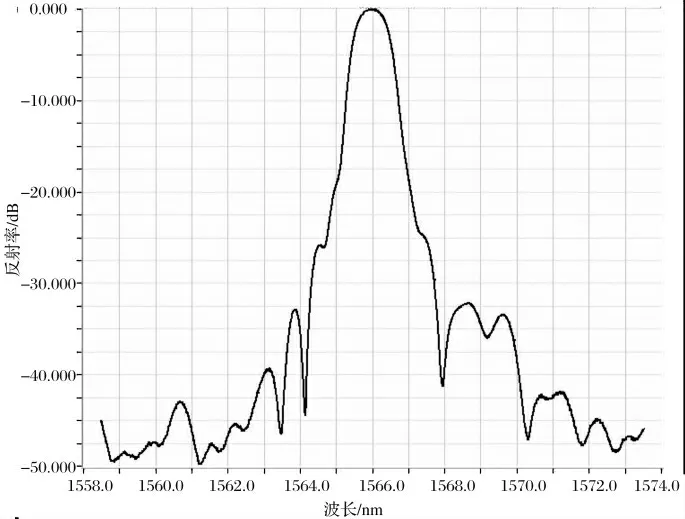
图8 Tanh 型2 mm 光栅反射谱

图9 Cauchy 型2 mm 光栅反射谱

刻制实验得到的光栅各项性能参数如表2 中所示。

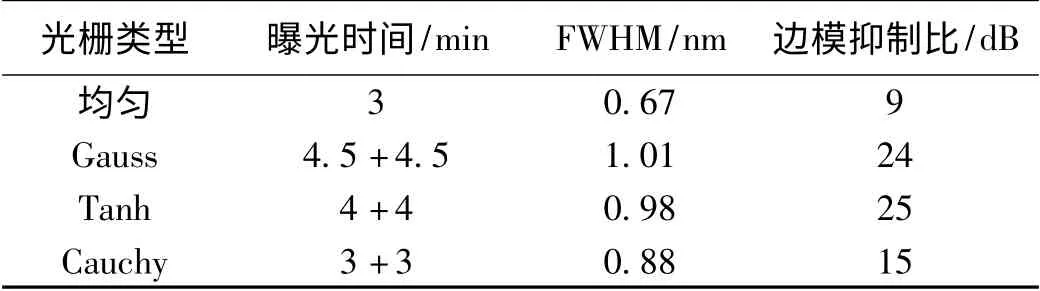
表2 二次曝光2 mm 光栅实验结果性能参数对比

以实验制作结果来看，二次曝光切趾光栅性能较均匀光栅提升显著，在85% 较高反射率下可以满足FWHM ＜1.5 nm 及较高的边模抑制比要求。均匀光栅的带宽较仿真结果略有提升，边模抑制比由21 dB 下降至9 dB。Gauss 型、Tanh 型光栅边模抑制性能较高，达到25 dB 附近，图谱形状对称。Cauchy 型FWHM 最小，但边模抑制比提升性能有限，在15 dB 附近，亦可满足使用需求，且图谱形状最为规则对称，反射主峰陡峭。但切趾光栅的制作时间要远远长于均匀光栅，为保证光栅的优良光学性能，需严格控制实验环境条件，最大限度的隔绝振动等因素影响。实验结果看来，所设计2 mm 切趾光栅均可以满足传感使用需求。

4 结束语

本文从传感用2 mm 短栅距型二次曝光切趾光栅的光谱优化的角度，利用传输矩阵法通过数值方法模拟分析了3 种切趾函数下2 mm 短栅距型FBG 的反射特性，并进行了制作实验。仿真分析的结果表明，在最佳参数下的切趾型2 mm 栅距光栅性能较均匀光栅提升显著，在85%的高反射率下保持较低带宽，并大幅度的提升了边模抑制比。同时，可以得到一般性结论:反射谱的旁瓣抑制反射谱的带宽提升和反射图形梯形化为代价的，在选择切趾函数和相应的切趾函数参数的时候要对上述因素综合考虑。

［1］饶云江，王义平，朱涛. 光纤光栅原理及应用［M］. 北京:科学出版社，2006.

［2］ Raman Kashyap. Fiber Bragg Gratings ［M］. 2nd ed. Salt Lake City:Academic Press，2009.

［3］刘伟平，杜戈，黄君凯，等. 光纤布拉格光栅反射谱旁瓣的抑制［J］. 激光与红外，2001，31 (3)52 －55.

［4］贺园，卢会群. 光纤Bragg 光栅光谱特性研究［J］. 桂林电子科技大学学报，2009，29 (6):12 －15.

［5］于志辉，余重秀，王葵如，等. 直流切趾对光纤光栅特性的影响［J］. 光学精密工程，2006，14 (6):7 －10.

［6］吴霞，冉洋，刘伟平，等. 基于二次曝光切趾技术的光纤光栅边模抑制性能研究［J］. 仪表技术与传感器，2010(5):69 －70.

［7］赵岭，瞿荣辉，李琳，等. 基于莫尔效应的光纤光栅变迹的研究［J］. 中国激光，2003，30 (12):1103 －1106.

［8］Zongqiang Lin，Xiangfei Chen，Fei Wu，et al. A novel method for fabricating apodized fiber Bragg gratings ［J］. Optics ＆Laser Technology ，2003，35:315 －318.