基于自适应滤波的相位起伏控制方法

付霖宇，张鑫，曹建，崔欣辰，程永茂

(海军航空工程学院 兵器科学与技术系，山东 烟台264001)

0 引言

在指挥、控制、通信等信息系统中，为了实现时间统一，往往采用GPS 标准信号来对本地频标进行校频［1］。在复杂电磁环境及作战节点快速移动的情况下［2］，GPS 授时校频系统引入大量噪声，输出信号的相位随噪声调制起伏，引起频率的随机起伏，短期抖动较大［3］，因此亟需解决相位起伏的控制问题。

本文提出一种基于自适应滤波的相位起伏控制方法，通过寻找滤波系统的最优传递函数进行阈值设定，抑制调制噪声，并采用Widrow-Hoff LMS 算法［4］，降低信号相位起伏频谱中无规律游走噪声所占的比重，减少运算的复杂度，提高数据处理的时效性，实现对输出信号相位起伏的稳定控制。

1 GPS 授时校频

目前主流的GPS 接收机能够输出相对协调世界时(UTC)能够输出误差小于50 ns 的秒脉冲(1pps)信号［5］。GPS 授时校频原理如图1 所示。测量GPS 输出的标准信号与本地频标输出的1pps 信号的时间间隔，得到的时差测量数据经鉴相器转换为两信号的相位差，按照相位差的变化速率计算得到相对频差，经处理器存储、数模转换、相位电压转换，输入压控端口完成锁相环回路控制，使本地频标同步于GPS 时钟。在整个回路中，鉴相控制是稳定本地频标输出信号与GPS 标准信号相位差的重要环节，本文将重点研究其实现方法。

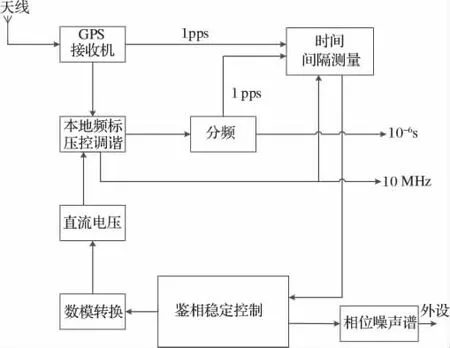
图1 GPS 授时校频原理框图

2 基于自适应滤波的相位起伏控制

采用高精度时间间隔测量技术可以显著提高GPS标准信号和本地频标输出信号相位差的准确性［6］。在此基础上，尚需解决相位差的稳定性问题。最小均方(LMS)自适应算法［7］能通过有效抑制调制噪声来提高信噪比，不需要关于输入信号的先验知识，计算量小，特别适用于实时处理。

自适应滤波算法的关键是进行阈值设定，阈值的作用是对含噪声信号进行门限设定。若信号估计的误差表示为，则依据最小均方误差准则，需使最小。因此，可以把阈值设定看成一个寻找滤波系统的最优传递函数的过程。采用物理可实现条件约束的设计思想，求出这个传递函数的最优解Hopt(ejω)，从而实现最小均方意义下的自适应滤波。

含噪的信号模型可表示为

式中:x(t)为含噪信号;s(t)为GPS 标准信号;v(t)为噪声，且v(t)与s(t)不相关。根据谱估计理论，最优传递函数可表示为

式中:φxs(ejω)是含噪信号x(t)与GPS 标准信号s(t)的相关函数;φxx(ejω)是含噪信号x(t)的自相关函数。因为v(t)与s(t)不相关，所以φxs(ejω)= φss(ejω)，即φxx(ejω)= φss(ejω)+ φvv(ejω)，所以有

考虑到在实际中要求信号是物理可实现的，因此对Hopt(ejω)的求解要受到因果条件的约束。即

式中:σ2ν(ejω)为噪声信号的方差;B(ejω)是由φxx(ejω)在单位圆内的零极点组成;B(e－jω)是由φxx(ejω)在单位圆外的零极点组成;[ ·]+表示因果条件。为了提高对数据的处理速度，采用Widrow-Hoff LMS 算法(最陡下降法)进行阈值设定，示意图如图2。该自适应阈值设定方法通过状态空间和递推的形式描述系统，不需要过去的全部观测数据，仅需根据前一次的估计值和最近一个观测数据实现对当前阈值的估计，减少了运算的复杂度，提高了数据处理的时效性。

图2 Widrow-Hoff LMS 自适应阈值设定

3 分析和结论

根据当前器件发展的实际情况［8－9］，仿真参数设置如下:本地频标标称值f0= 10 MHz，频率稳定度3 ×10－11，频率准确度5 × 10－11，电子计数器频率10 MHz，数据输出信噪比65 dB。为了克服信号在相位微分过零点(90°和270°)处受采样误差影响较大的问题，采用同频正交信号样式。运用Simulink 工具进行动态数据仿真，得到相位误差与GPS 接收机ADC 量化位数的关系如表1。

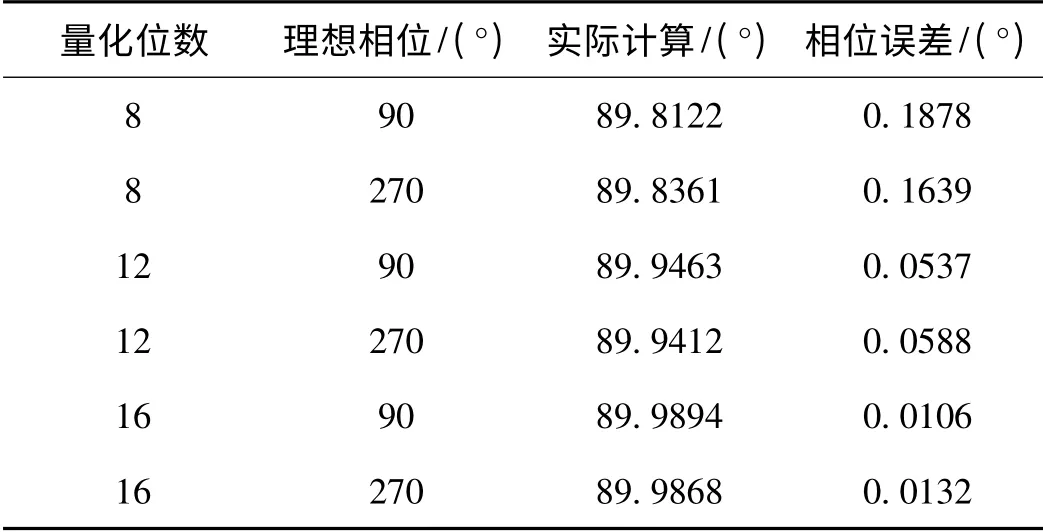
表1 10 MHz 正交信号90°处的相位误差

可见，采用自适应滤波相位起伏控制的正交信号具有较高的相位提取精度，当量化位数达到10 位以上时，可保证相应的时间提取精度达到ps 量级［10］。该方法对输出信号相位稳定性的改进效果可由相位起伏谱密度 Sφ(f)来表征［11］，通常采用对数坐标，即logSφ(f)～log f 的形式，如图3。

输出信号相位起伏谱密度随傅氏频率的变化关系表明:

1)相位起伏谱密度按幂指数规律变化。在低频部分，噪声调制主要受无规律游走噪声的影响，频谱图上体现为大斜率的直线谱，Sφ(f)与f4成反比，在中频和高频部分，白噪声调制占主要影响，频谱图上体现为近乎水平的直线谱，Sφ(f)与f0成反比。

图3 输出信号相位起伏谱密度

2)与直接鉴相相比，自适应滤波算法可以进一步减少无规律游走噪声调制的影响。频谱图中白噪声替代了占有较大比重的无规律游走噪声，压缩了信号调制带宽，简化了噪声调制形式，从而在不影响输出信号分量的前提下，稳定了相位起伏，提高了相位提取精度。

本文通过对GPS 授时校频鉴相控制模块的研究和分析，建立了自适应滤波数学模型，提出Widrow －Hoff LMS 相位起伏控制方法，简化了噪声调制形式。仿真和实验结果表明，该方法明显减少了传统直接鉴相过程中无规律游走噪声对相位起伏的影响，提高了相位提取精度，较好地实现了本地频标输出频率与GPS 标准信号的稳定统一，在工程实现方面可为各项任务提供更准确、可靠的时间频率信号。

［1］童宝润. 时间统一系统［M］. 北京:国防工业出版社，2003:2 －7.

［2］谭显春，陈璇. 舰载作战系统时间统一技术构想［J］. 舰船电子工程，2006，26 (6):12 －15.

［3］王江安，庄奕琪，周清军，等. 利用改进卡尔曼滤波算法抑制GPS 接收机相位噪声［J］. 数据采集与处理，2010，25 (5):611 －614.

［4］高鹰，谢胜利. 一种变步长LMS 自适应滤波算法及分析［J］. 电子学报，2001，29 (8):1 －4.

［5］曾亮，孟庆杰，徐伟. 利用GPS 驯服校频技术提高晶振性能［J］. 计量技术，2008 (5):6 －8.

［6］潘继飞，姜秋喜，毕大平. 基于内插采样技术的高精度时间间隔测量方法［J］. 系统工程与电子技术，2006，28(11):1633 －1636.

［7］李智慧，关宗安. 一种改进的LMS 算法及其在自适应消噪中的应用［J］. 沈阳航空工业学院学报，2006 (2):65－67.

［8］杨旭海，翟惠生，胡永辉，等. 基于新校频算法的GPS 可驯铷钟系统研究［J］. 仪器仪表学报，2005，26 (1):41－44.

［9］赵军祥，李建辉，常青，等.GPS 授时校频方法研究与试验结果［J］. 北京航空航天大学学报，2004，30 (8):762－766.

［10］朱祥维，孙广福，雍少为，等. 利用相位估计算法实现ps量级的时间间隔测量［J］. 仪器仪表学报，2008，29(12):2626 －2631.

［11］马凤鸣. 时间频率计量［M］. 北京:中国计量出版社，2009:31 －35.