反舰导弹协同攻击目标分配与在线再分配方法研究*
李红亮,刘 铁,宋贵宝
(海军航空工程学院,山东烟台 264001)
0 引言
传统的反舰导弹武器目标分配,都是在射前根据目标探测信息,由指控中心确定要打击的目标和攻击给定目标的导弹数[1-3],分配的前提假设是反舰导弹能够精确地飞到预定位置,目标编队作匀速直线运动。然而战场环境是动态变化的,导弹飞行存在散布误差,目标编队队形、位置、航向、航速都可能发生变化,因而导致预先分配的结果可能不再是优的。为此,文中提出了分段目标分配的思想,将反舰导弹整个飞行过程分为两段,按段进行预先分配和在线再分配。针对分配时机不同和追求的优化性能指标不同,构建了综合考虑多种因素的分段目标分配优化模型。
反舰导弹目标分配问题是一个约束众多而复杂的优化问题,其解空间随目标总数的增加而呈指数增加。传统的求解方法是将该问题简化为数学规划模型,然后采用穷举法、动态规划、分支定界等方法进行求解。然而问题的求解受维数的限制,当问题的维数增加时,运算复杂度将成指数增加,很难得到最优解。智能算法在求解该问题时取得了较好的效果,包括遗传算法[4]、遗传模拟退火算法[5]、蚁群算法[6]、粒子群算法[7]及它们的混合算法[8-10]等。然而这些算法并没有关注目标分配给导弹航路规划带来的影响,即在编码设计时没有考虑优化结果会造成导弹航路交叉现象的发生。为此,文中提出了一种离散粒子群算法,并针对各段分配模型,设计了不同的解编码方式、粒子初始化方法和适应度函数。改进的编码和粒子群初始化方式,避免了多导弹弹道交叉和初始粒子群中由于存在大量非可行解而导致搜索效率降低的问题。通过引入变异、交叉等遗传算子,增加了解的多样性并加快了解的收敛速度。
1 战局假设
攻击方舰艇编队S由NS艘舰组成,舰艇Sk(Sk∈S,k=1,2,…,NS)携载智能化反舰导弹数为 nk,令;目标舰艇编队T由 NT艘舰组成(其中Tj∈T,j=1,2,…,NT)。攻方编队在获知战场和目标信息后,由指控中心根据敌我双方兵力组成、预定的作战目的,确定作战要达成的毁伤效果,然后利用以弹药消耗量为优化指标的目标分配模型计算完成任务所需求的弹药量(假设为 NM2,类型相同且 NM1≥NM2≥NT),并对NM2发反舰导弹进行协同航路规划。导弹发射后在预定时刻由事先确定的一枚反舰导弹作为领弹升空探测目标,当探测到目标后将目标信息通过数据链传回指控中心,指控中心根据目标编队队形、位置、航向与航速以及反舰导弹编队各弹位置、飞行方向,对导弹要打击的目标重新进行分配,然后根据分配结果对弹群分组并设置导弹选择目标模式。
2 约束条件分析
反舰导弹协同攻击目标分配必须满足相关的约束条件,包括:
1)任务兵力数量约束:在一次作战任务当中,反舰导弹的总数目是一定的,因此反舰导弹发射数量不能超过舰艇编队携载的数量。
2)攻击舰与目标舰的配对关系约束:为防止导弹发生碰撞或导引头的相互干扰,应避免航路交叉,并且使各导弹攻入角度保持一定的差角。这就需要根据敌我双方编队位置、队形对攻击舰与目标舰进行合理配对。
3)目标最小联合毁伤概率约束[11]:为了防止目标分配结果片面追求性能指标最优,而过分趋于分散射击,导致对各目标的毁伤等级平均且较低,达不到震慑敌方心理和预定作战效果的目的,一般情况下,在下达作战任务时会同时要求对某些目标的毁伤概率或毁伤度达到一定的阈值,即对目标的毁伤概率应该不小于指定的概率阈值。
4)目标最大联合毁伤概率约束:多反舰导弹协同作战的效果不仅取决于单枚反舰导弹的作战效能和对单个目标的作战毁伤概率,更主要的在于多枚反舰导弹的整体作战效果,期望在对单个目标达到一定毁伤概率的同时,兵力不应过度集中于单个目标,即对同一目标实施攻击的反舰导弹数目不能太多。而如果通过限制攻击同一目标的反舰导弹最大个数来实现分散兵力的目的,由于每枚反舰导弹对每个目标的毁伤概率不完全相同,最大个数约束值很难选取,因此文中采用目标最大联合毁伤概率加以约束。
3 模型的建立
由于目标分配时机不同,追求的优化性能指标也不同,通常反舰导弹目标分配可以分为两种:1)在确定目标毁伤价值条件下,极小化弹药消耗量;2)在一定弹药消耗量条件下,极大化目标毁伤价值。反舰导弹发射前的预先目标分配重点关注的是根据敌我兵力、作战目的确定导弹发射总数量和各舰发射数量,适合利用第一种目标分配模型求解;导弹发射后,弹药消耗量已经确定,为了应对战场态势变化需进行在线目标重新分配,其目的就是极大化目标毁伤价值,使得整个导弹群的作战效能和任务成功率最高,因此在线目标重新分配适合利用第二种目标分配模型求解。
根据追求的优化性能指标和相应的分配约束条件,文中分别建立两种情形下的目标分配模型。第一种情形即极小化弹药消耗量建立目标分配优化模型如下:
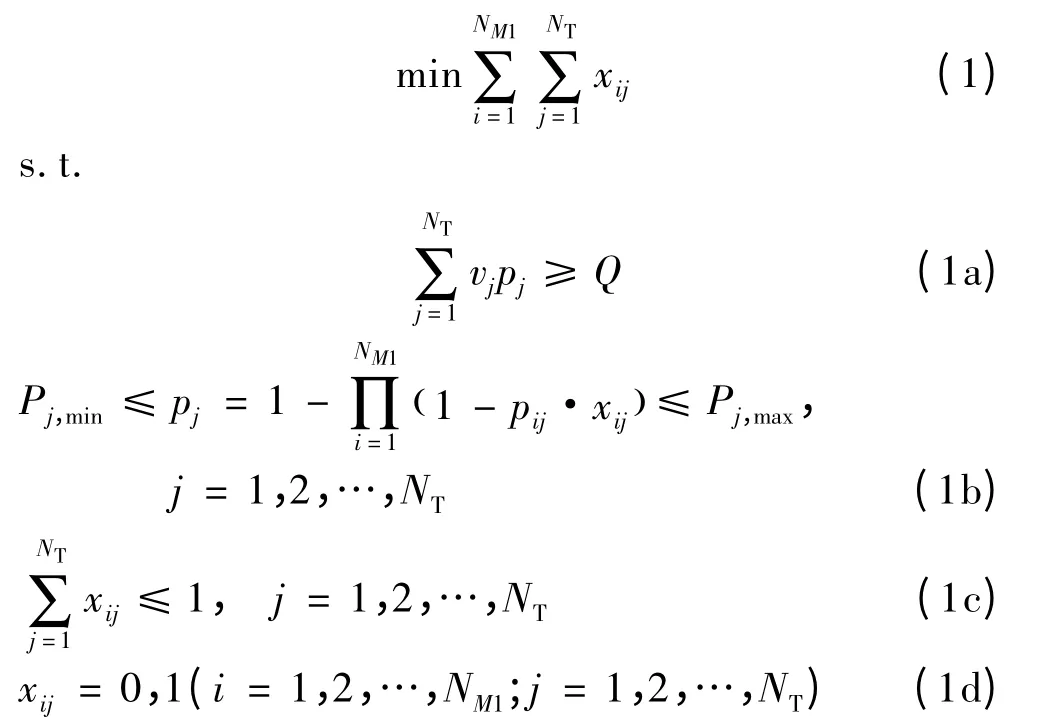
式中:Q为攻方编队计划获得的毁伤目标价值的收益;xij为决策变量,xij=1表示将第i发导弹分配给第j艘舰船,xij=0则表示不分配;vj表示敌编队第j艘舰艇的价值;pij为第i发反舰导弹对敌编队第j艘舰艇的毁伤概率;pj为反舰导弹对敌编队第j艘舰艇的联合毁伤概率;Pj,min、Pj,max分别为反舰导弹对第 j个目标的最小和最大联合毁伤概率门限。
第二种情形即极大化目标毁伤价值建立目标分配优化模型如下:

式(2a)中对目标联合毁伤概率没有施加最大门限约束,原因是在目标函数的作用下,计算结果肯定将趋向于分散射击,没必要再施加该约束。
4 基于离散粒子群算法的目标分配求解
因为标准的粒子群算法具有连续本质,不太适宜于求解离散问题。因此,文中将离散粒子群算法用于反舰导弹目标分配问题的求解。
4.1 解的编码方式
反舰导弹目标分配的关键在于确定每发导弹攻击哪个目标或者某个目标被哪发导弹攻击,因此,这里采用自然数编码方式来表达,而且有两种编码方式。
1)以导弹发射数量为基
每个粒子长度等于反舰导弹发射总数,粒子由按导弹编号顺序排列的目标分配编号组成,表示一种可能的分配方案。例如,假设反舰导弹数目n取6,目标舰艇数目m取3,一个粒子为:
粒子
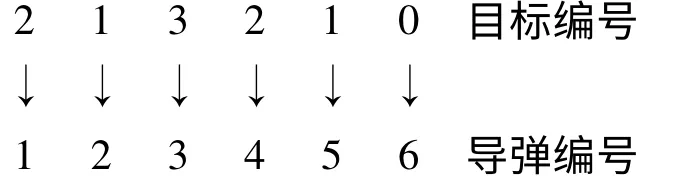
表示第1发导弹攻击第2个目标,第2发导弹攻击第1个目标,…,第6发导弹不攻击任何目标即不发射。保证约束条件中对每发导弹至多分配一个目标的限制,粒子取值范围为[0,m]。
该编码方式的优点是可以清晰地看出每发导弹是否发射并攻击目标、攻击哪个目标;缺点则是编码较长,优化搜索时间会较长,且不便于满足防止导弹航路交叉的要求。因此该编码方式适用于导弹发射前预先分配问题的求解,允许稍长的搜索时间,且通过调整发射顺序可以避免导弹航路出现交叉的现象。
2)以目标舰艇数量为基
每个粒子长度等于目标舰艇总数,粒子由按目标编号顺序排列的导弹分配数量组成,表示一种可能的分配方案。例如,假设反舰导弹数目n取6,目标舰艇数目m取3,一个粒子为:
粒子

表示攻击第1个目标的导弹数量为2,攻击第2个目标的导弹数量为3,攻击第3个目标的导弹数量为1。保证约束条件中对攻击所有目标的导弹和为发射导弹数的限制,粒子取值范围为[0,n]。
该编码方式的优点是编码短,将节省优化搜索时间,适合用于在线目标重分配问题的求解。针对由于每发导弹对目标的毁伤概率不同,需要对攻击同一目标的多发导弹进行区分的问题,文中采用平面扫描的方法予以解决:指控中心根据领弹探测到的目标信息和对反舰导弹的定位信息,顺着导弹飞行方向观察,按照导弹位置从左至右依次编号,目标位置也按从左至右依次编号,当给最左方第1个目标分配3发导弹时,即编号为1、2、3的导弹被分配给1号目标。
4.2 粒子群初始化
粒子群中的每一个粒子对应于待解决问题的一个可行解,因此在目标分配问题中粒子的表示就是一个可行的分配方案。粒子群粒子数量的大小M对算法的运行效率和效果有一定的影响,当M取值过大时会降低算法的运行效率;而M取值过小时,可以提高算法运行速度,但降低了粒子群的多样性,算法易早熟收敛。一般M取值为30~60之间为宜。
1)以导弹发射数量为基
令反舰导弹数为n,目标舰艇数为m,粒子位置Z=(z1,z2,…,zn),zi(i=1,…,n)的物理含义为第i发导弹攻击目标的编号,其值确定方式为:
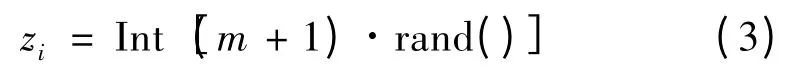
式中:rand()为区间[0,1]上的随机数,Int[·]为取整函数。
2)以目标舰艇数量为基
粒子位置 Z=(z1,z2,…,zm),zi(i=1,…,m)的物理含义为攻击第i个目标的导弹数量,其值确定方式为:

3)粒子重复性和可行性检验
每产生一个粒子,均要判断是否与之前生成的初始粒子是否相同,如果相同就要舍弃,避免初始粒子群中存在多余的重复粒子。另外,还要进行可行性检验,针对每个新生成的粒子,建立以xij为决策变量的决策矩阵,并逐一判断粒子是否满足目标分配优化模型中的约束条件。
4.3 适应度函数值的计算
根据两种目标分配优化模型和解的编码方式,分别建立针对预先目标分配和在线再分配的适应度函数。
1)预先规划段目标分配

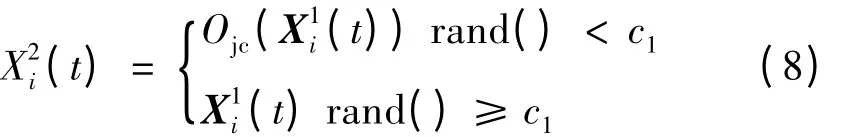
交叉操作的实现方法是由rand()产生一个区间[0,1]上的随机数r:如果r<c1,将对粒子进行交叉操作,即产生2个在[1,L]之间不同的随机数 a和 b,然后将X1i(t)矢量第a个与第b个之间的数值替换为pi(t)矢量第a个与第b个之间的数值;如果r≥ω,则不进行交叉操作。交叉过程如图1所示。
2)重规划段目标分配
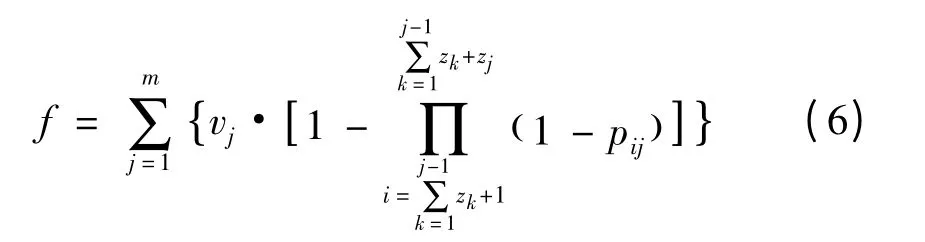
4.4 个体更新
离散粒子群算法中的粒子更新策略是此方法的核心,对粒子个体进行更新主要采用了遗传算法中的交叉算子、变异算子,它们的采用避免了有关参数的选择,也不必使用粒子的速度,变得更易操作,同时也保持了算法的全局搜索能力。假设粒子长度为L,粒子的更新操作步骤如下:
1)粒子的惯性飞行
粒子的“惯性”部分,表示粒子对自身飞行速度的思考。设ω为惯性权重,Xi(t)为粒子i在t次迭代中的位置,粒子“惯性”部分的操作公式为:
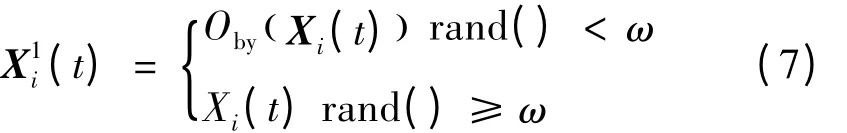
变异操作的实现方法是由rand()产生一个区间[0,1]上的随机数 r:如果 r<ω,将对粒子进行变异操作,即产生2个在[1,L]之间不同的随机数 a和 b,然后将粒子位置矢量的第a个数值与第b个数值互换;如果r≥ω,则不进行变异操作。
2)粒子的“认知”学习
粒子的“认知”部分,表示粒子根据个体极值Pi(t)调整自身的位置。设 c1为认知系数,粒子“认知”部分的操作公式为:
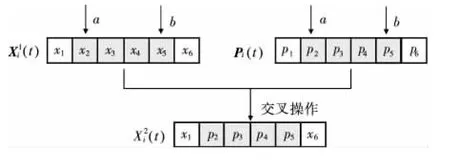
图1 与个体极值交叉操作
3)粒子的“社会”学习
粒子的“社会”部分,表示粒子根据全体极值Pg(t)调整自身的位置。设 c2为社会系数,粒子“社会”部分的操作类似于粒子“认知”部分的操作,在此不再赘述。
4)交叉操作后的可行性处理
粒子在进行“认知”学习或“社会”学习后,新的粒子可能是非可行解。对于预先目标分配的粒子编码方式,出现非可行解的原因是更新后的粒子不满足公式(1a)、(1b)中的约束条件;对于在线再分配的粒子编码方式,出现非可行解的原因是更新后的粒子不满足公式(2a)中的约束条件以及粒子各位置的和不等于反舰导弹的发射总数。
对于不满足公式(1a)、(1b)或(2a)约束条件的粒子予以删除,使之不能参与信息素的更新。
对于不满足反舰导弹发射总数要求的粒子,进行如下改造:①当新解a、b之间数值之和小于旧解a、b之间数值之和,可将差额加在新解b位置的数上;②当新解a、b之间数值之和大于旧解a、b之间数值之和,首先由新解b位置的数开始减去差额,如果b位置的数小于差额,则将b位置的数减为0,再由b-1位置的数减去剩下的差额,依次类推,直到把差额全部减完。
5 仿真实验
5.1 仿真运行参数
仿真计算机配置:运行环境为 Windows XP,CPU为 Intel(R)Pentium(R)Dual E2200,主频 2.20GHz,内存1GB。基于以上的参数设置及系统配置,在Matlab6.5环境下,采用离散粒子群算法分别对各规划段目标分配进行优化搜索仿真。设运算终止代数为100,ω =c1=c2=0.5,运行次数为 100。
设目标舰艇的造价为 ZJ=(0.35,0.2,0.25,0.2,0.2),权重为 0.25;目标的任务价值为 RW=(0.35,0.2,0.3,0.3,0.2),权重为 0.45;目标的威胁程度为WX=(0.35,0.1,0.3,0.25,0.15),权重为0.30。
5.2 预先分配
假设我舰艇编队携载20发某型反舰导弹,敌舰艇编队由1艘驱逐舰、4艘护卫舰组成(编号分别为1~5),我编队导弹攻击效果要求对敌编队的最低毁伤概率为(0.6,0.5,0.5,0.5,0.5),为防止集中射击要求最高毁伤概率为(0.9,0.8,0.8,0.8,0.8)。预先目标分配时单发反舰导弹对目标的毁伤概率随机产生:对驱逐舰的单发毁伤概率取0.1~0.2之间的随机数;对护卫舰的单发毁伤概率取0.2~0.3之间的随机数。
经仿真得,预先目标分配结果为(4,0,1,1,3,0,1,1,1,0,5,0,3,2,0,2,4,4,5,2),适应值即最小弹药消耗量为 15,耗时 128.45s。
5.3 在线再分配
根据预先分配结果,我编队发射15发反舰导弹对敌编队实施协同攻击,在线再分配所需的毁伤概率经蒙特卡洛仿真计算获得并作为后期算法输入数据(见表1)。

表1 反舰导弹对目标的毁伤概率
经仿真得,在线再分配结果为(4,4,2,3,2),适应值为 0.7604,对各舰的毁伤概率为(0.7123,0.6254,0.5036,0.5730,0.5520),耗时 3.78s。
6 结束语
文中从反舰导弹作战实际出发,考虑导弹飞行偏差和目标运动等动态因素对目标分配的不利影响,提出了目标预先分配和在线再分配分段规划的思想。针对分配时机不同和追求的优化性能指标不同,构建了综合考虑多种因素的分段目标分配优化模型。利用离散粒子群算法建立了粒子与实际问题的映射,通过改进编码和粒子群初始化方式解决了目标分配整数约束和多导弹弹道防交叉的问题。通过交叉、变异等遗传算子对粒子个体进行更新,既增加了解的多样性,又加快了解的收敛速度。
预先分配解决了兵力需求以及火力粗略分配的问题,获得了确定打击效果条件下的最小弹药用量,为在线再分配提供了初始条件;在线再分配则根据战场实际态势对初次分配进行了实时修正。经过大量仿真计算,表明文中模型和算法可快速有效地用于求解反舰导弹协同攻击目标分配问题。
[1]张晓锐,汪小娜.基于多维动态规划的空舰导弹最优火力分配模型[J].弹箭与制导学报,2004,24(1):94-96.
[2]张年春,沈培华.编队导弹攻击的火力分配研究[J].战术导弹技术,2007(3):36-39.
[3]杨飞,董朝阳,王青.实施饱和攻击的反舰导弹武器目标分配[J].系统仿真学报,2011,23(2):316-320.
[4]Shima T,Rasmussen S J,Sparks A G. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms[J]. Computers and Operations Research,2006,33(11):3252 -3269.
[5]Wang Jun,Zhu Yongwen. A solving algorithm for target assignment optimization model based on SA[C]//International Conference on Artificial Intelligence and Computational Intelligence,2010:489 -493.
[6]Zhang Limin,Zhang Yuan,Liu Wenbiao. The design of target assignment model based on the reverse mutation ant colony algorithm[C]//International Workshop on Information and Electronics Engineering,2012:1554 -1558.
[7]高尚,杨静宇.武器-目标分配问题的粒子群优化算法[J].系统工程与电子技术,2005,17(7):1250 -1252.
[8]AlRashidi M R,El-Hawary M E. Hybrid particle swarm optimization approach for solving the discrete OPF problem considering the valve loading effects[J]. IEEE Transactions on Power Systems,2007,22(4):2030 - 2038.
[9]陈华东,王树宗,王航宇.基于混合粒子群算法的多平台多武器火力分配研究[J].系统工程与电子技术,2008,30(5):880-883.
[10]叶文,朱爱红,欧阳中辉,等.基于混合离散粒子群算法的多无人作战飞机协同目标分配[J].兵工学报,2010,31(3):332 -336.
[11]郭蕴华,李运涛,杨福缘.考虑毁伤概率门限的火力分配变异蚁群算法[J].火炮发射与控制学报,2006(4):1-5.

