涵道共轴双旋翼空气动力学特性分析

杨加明，戴良忠，丛 伟

(南昌航空大学飞行器工程学院，南昌 330063)

0 引言

共轴反桨涵道无人机与传统的无人直升机相比，有其独特的优点。首先，在同等功率消耗下，其产生的拉力要大于孤立的旋翼系统，原因是涵道本体提供了相当一部分升力。其次，上下旋翼共轴反桨，产生的反向扭矩可以相互抵消，省去了无人直升机的尾桨。再则，涵道结构使无人机结构更加紧凑，低空飞行安全性高，噪声低，隐蔽性好。

国外关于单旋翼涵道无人机的研究已经相当成熟[1－2]。对于共轴双旋翼的理论计算也由来已久，早先采用滑流理论[3]，后来发展到预定尾涡模型[4－5]，再后来发展到自由涡模型[6]。国内的童自立、孙茂[7]采用了动量源项法对双旋翼的干扰流动进行了Navier-Stokes(N-S)方程数值计算，将旋翼对流场的影响用桨叶施与流体的动量来计及，在N-S方程中引入动量源项。动量源项法基于流场解，可较好的描述尾涡系的畸变和两旋翼尾迹的干扰。但滑流理论无法计及尾迹畸变，预定尾涡模型需要用实验给出尾迹，自由涡模型也不能很好的给出尾迹和两旋翼的干扰作用，无法对桨叶附近的细致流动和尾迹中的桨叶涡系进行模拟。许和勇、叶正寅[8]利用非结构动态嵌套网格方法，通过求解三维非定常Euler方程对悬停共轴双旋翼直升机的复杂流场进行了数值模拟，探讨两旋翼相互干扰的特性及有关参数的影响。

但对于共轴反桨涵道无人机的研究并不多见。文中针对涵道共轴双旋翼机构中上下旋翼间距与拉力分配之间的关系做出相应研究，确定其变化规律。

1 计算方法

计算模型及网格模型都进行了一定程度的简化。因模型为中心对称结构，所以只需对四分之一模型进行分析。

计算域大小为实体的十倍，进出口边界条件分别为压力进出口，上下旋翼计算区域之间以及上下计算区域与外计算域之间采用Interface边界条件进行信息交换，分割面使用周期性边界条件。

当上下旋翼转速达到4000r/min时，桨尖的最大速度接近0.5～0.8Ma，计算区域作为理想可压缩气体处理。

考虑到计算模型同时存在运动区域和静止区域，文中利用FLUENT流体分析软件，在 MRF模型下采用有限体积法数值求解三维可压流N－S方程，通用稳态控制方程为:

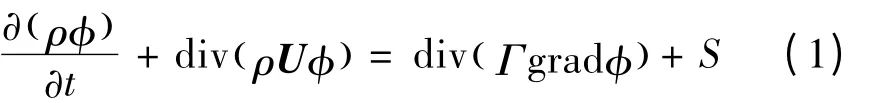
其中:

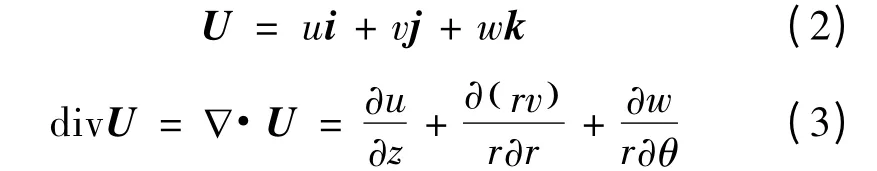
将式(1)展开，可以得到:

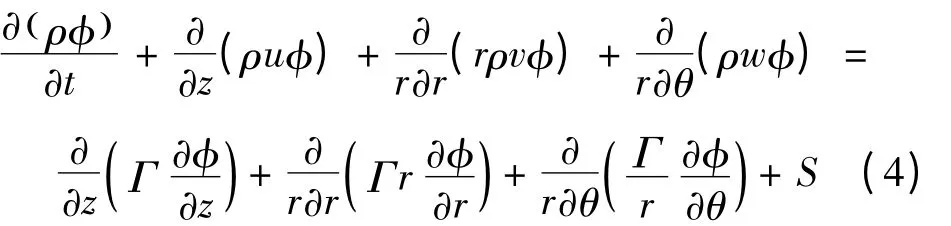
式中:φ表示通用变量，在三维柱坐标下可以是轴向速度u、径向速度v、周向速度w以及焓h;φ等于1代表连续方程;Γ为广义扩散系数;S为气相源项;U为速度矢量;ρ由完全气体状态方程确定。

控制方程的离散格式采用二阶迎风格式，即考虑了物理量在节点间分布曲线的曲率影响，其离散方程具有二阶精度的截差。此外利用二阶迎风格式可以促使单个方程不仅包含有相邻节点的未知量，还包括相邻节点旁其他节点的物理量。

计算的收敛情况通过监测变量的残差和质量流率的方式来判断，设定残差收敛精度10－4，同时监测计算域出口的质量流率。监测结果显示残差曲线在达到10－3时，基本保持水平，同时计算域出口的质量流率变化甚微，其差值保持在10－4量级，所以可以判定收敛良好。

2 共轴双旋翼的气动特性分析

模型相应的数据参数如表1所示。对模型进行网格划分，如图1所示。

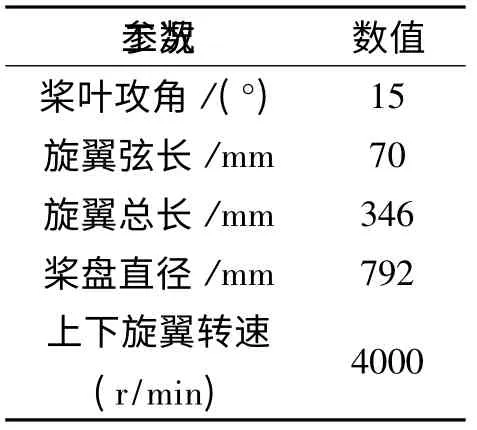
表1 NACA0014翼型模型尺寸与工况

图1 共轴双旋翼网格切片图

4种工况下的计算结果如表2所示。其中旋翼间距H/R为上下旋翼间距与旋翼桨盘直径之比;FN上为上旋翼产生的拉力;FN下为下旋翼产生的拉力;FN总为双旋翼产生的总拉力;T上为上旋翼扭矩;T下为下旋翼扭矩绝对值;FN上/FN总为上旋翼拉力占总拉力的比例。

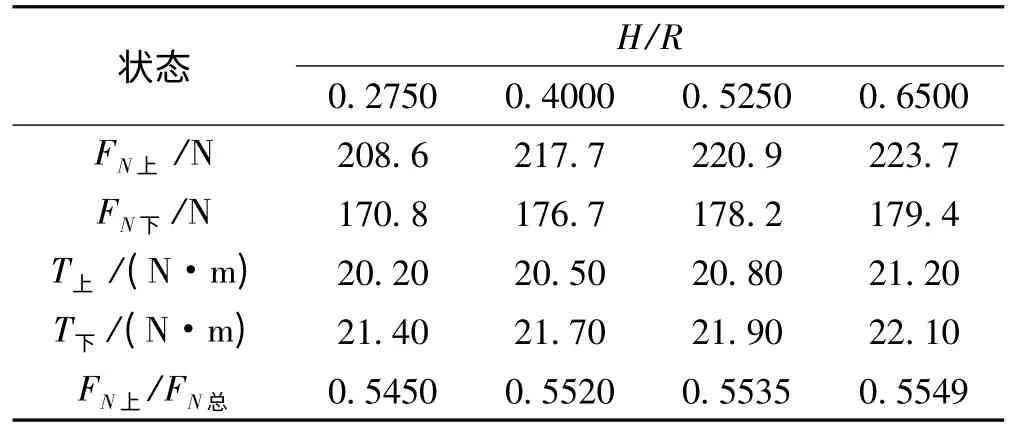
表2 共轴双旋翼拉力和扭矩

图2为共轴双旋翼速度矢量图。由图可以看出，上下旋翼之间存在着严重的气动干扰，即彼此的尾流作用。由于下旋翼处在上旋翼的滑流中，上旋翼的尾流穿过下旋翼，与下旋翼的尾流一起在下旋翼处产生下洗速度。同样下旋翼的尾流会在上旋翼处产生下洗速度，但作用明显小于上旋翼对下旋翼的影响。计算结果显示:上旋翼的拉力要大于下旋翼的拉力;随着H/R的增加，上下旋翼拉力均逐渐增大;下旋翼扭矩要略大于上旋翼。

上述分析结果同文献[7－9]中的结论相吻合，说明该方法适用于共轴双旋翼的气动分析。下面用同样的方法对涵道共轴双旋翼进行气动特性分析。

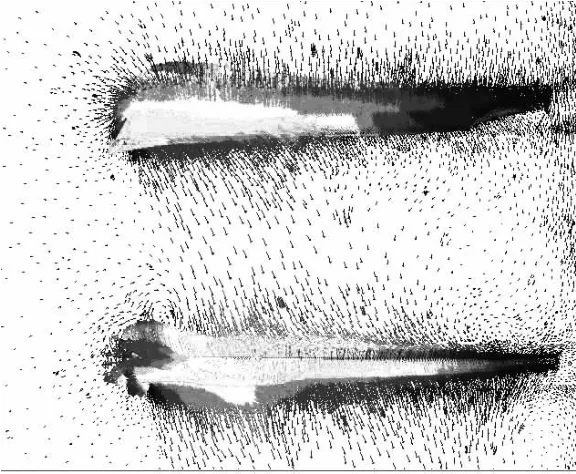
图2 共轴双旋翼速度矢量图

3 涵道共轴双旋翼的气动特性分析

为计算方便，对涵道共轴双旋翼模型做相应简化，如图3所示，模型尺寸与共轴双旋翼相同，涵道翼型选择NACA －66，高度330mm，内径 800mm，涵道壁最大厚度41mm。加上涵道后，旋翼与涵道内壁之间间距4mm。对于模型网格，将整个计算域分为4个子域网格。采用四面体非结构嵌套网格，对涵道和机翼部分进行网格加密，确保网格质量，网格数量在150万左右，如图4所示。

图3 涵道共轴双旋翼模型

同样对4种不同桨叶间距的涵道旋翼结构进行了数值模拟，计算结果如表3所示。表格中 Fd为涵道本体产生的拉力。

图4 涵道共轴双旋翼网格切片图

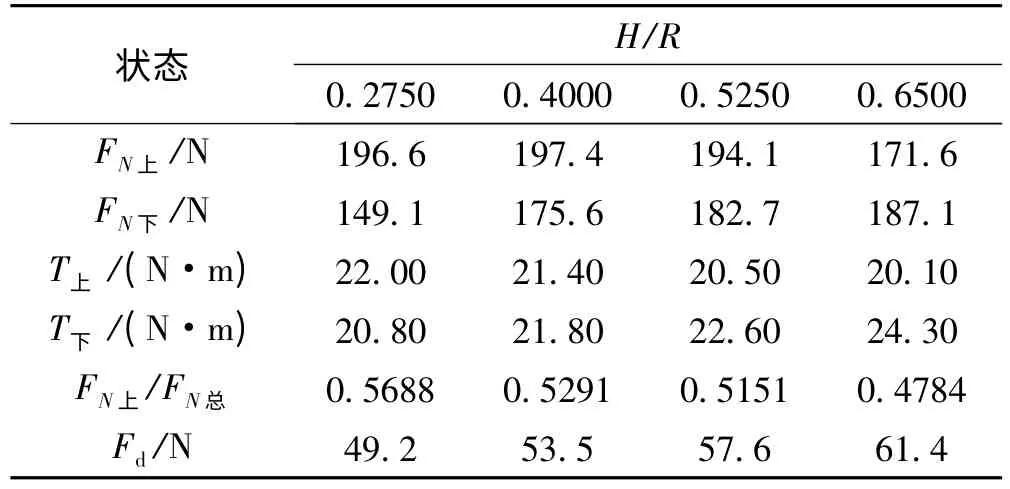
表3 涵道共轴双旋翼拉力和扭矩

4 对比分析

图5是涵道共轴双旋翼和孤立共轴双旋翼的旋翼拉力与旋翼间距之间的关系。可以发现，涵道共轴双旋翼的上旋翼拉力和总拉力均小于孤立共轴双旋翼。开始上旋翼拉力随着H/R增加而逐渐减小，并始终小于孤立共轴双旋翼的上旋翼拉力。涵道共轴双旋翼下旋翼拉力随着H/R的增加逐渐增大，当H/R增大到一定程度后，下旋翼拉力要大于共轴双旋翼的。涵道共轴双旋翼在H/R很小的时候，上旋翼拉力一直大于下旋翼拉力，这与共轴双旋翼结果相同。当H/R逐渐增大时，情况发生变化，下旋翼的拉力逐渐大于上旋翼的拉力，同时总拉力有所减少。

图6是旋翼扭矩与旋翼间距之间的关系。从图中我们知道，随着两旋翼之间距离的增大，涵道共轴双旋翼的上旋翼扭矩逐渐减小，下旋翼扭矩逐渐增加，而共轴双旋翼的上下扭矩均逐渐增大。观察图7中上旋翼拉力占总拉力的比值，可以发现，随着H/R的增大，孤立共轴双旋翼该比值略微增大;而涵道共轴双旋翼该比值在逐渐减小。

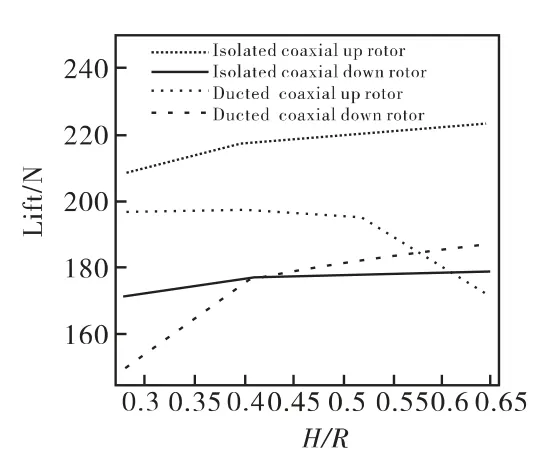
图5 旋翼拉力与旋翼间距之间的关系

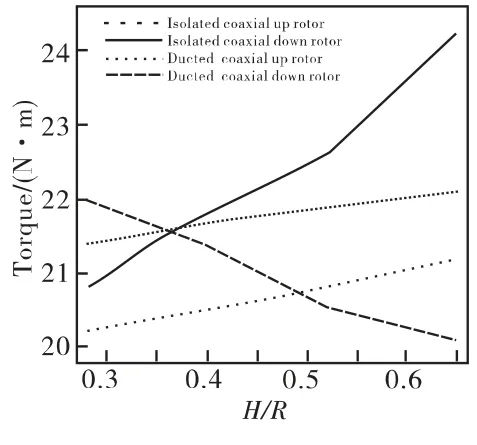
图6 旋翼扭矩与旋翼间距之间的关系

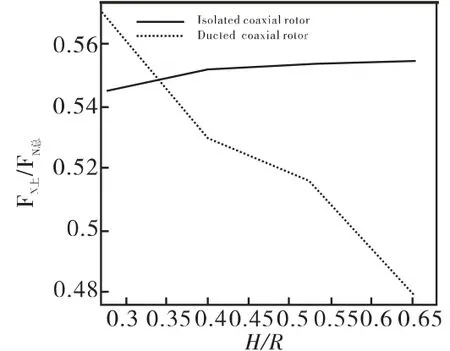
图7 FN上/FN总与旋翼间距之间的关系

文中将涵道当成一个环形机翼来处理[9]，所以涵道唇口剖面形状相当于翼型的前缘。图8是涵道共轴双旋翼的速度流线图。从图可以发现，旋翼的高速旋转产生了对外界气流的抽吸作用，并在涵道唇口产生绕流。该绕流在唇口附近产生一个负压区域，使涵道本体产生了一定的拉力。由上面分析所得结果可以看出，涵道本体产生的拉力与共轴双旋翼产生的拉力之和要大于孤立共轴双旋翼产生的总拉力。这一结论与文献[10]所证明的单旋翼涵道系统的结果类似。

由于研究的涵道本体翼型以及涵道结构参数并没有做进一步的优化设计，所以在文中显示的涵道本体产生的拉力并不大。同时文中研究的状态并没有实行前飞，所以涵道没有做倾斜，使得涵道本体产生拉力的能力没有得到更好的体现，但涵道共轴双旋翼的总拉力依然要大于孤立共轴双旋翼的总拉力。说明了涵道共轴双旋翼的工作效率比孤立共轴双旋翼的要高，即如果保持相同的拉力，涵道共轴双旋翼机构只需较小的输入功率。另外涵道本体实现了整体机构的隐身、飞行安全和噪音控制。

图9和图10分别为H/R=0.275和H/R=0.65时涵道共轴双旋翼速度矢量。从图可以看出，当H/R较小，也就是上旋翼离涵道上唇口距离较远时，涵道唇口绕流对上旋翼的影响较小。观察图10可以知道，随着H/R逐渐增大，上下旋翼之间的气动干扰随之减弱，上旋翼逐渐处于涵道唇口绕流内，使其气动特性发生很大变化，拉力不断下降，从而使下旋翼产生的拉力要大于上旋翼。

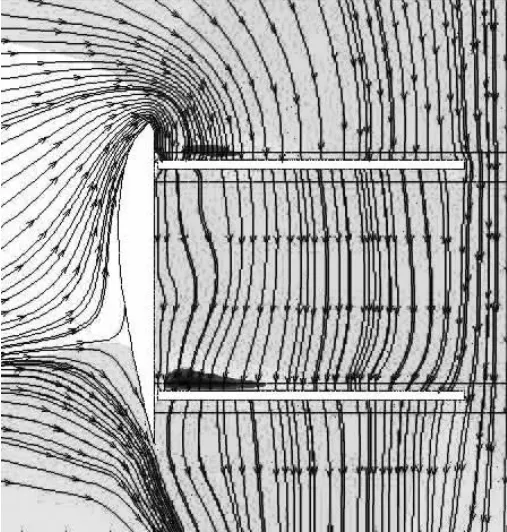
图8 涵道共轴双旋翼气流迹线

图9 速度矢量图(H/R=0.275)

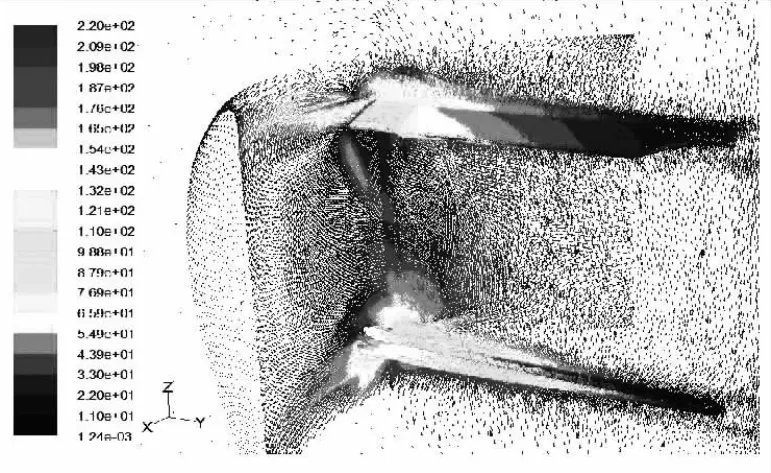
图10 速度矢量图(H/R=0.65)

在涵道飞行器设计过程中，需要考虑如下现象:即增大旋翼间距会导致上旋翼拉力和扭矩逐渐减小，甚至小于下旋翼拉力及扭矩，而扭矩的不平衡必将导致涵道飞行器产生旋转。所以要根据上下旋翼间距与拉力分配关系来确定适当的旋翼间距，以保证上下旋翼扭矩的差值可以通过调节旋翼攻角来控制。

5 结论

1)由于涵道本体的作用，涵道共轴双旋翼产生的旋翼拉力要小于孤立共轴双旋翼所产生的拉力，但如果加上涵道本体产生的升力，其总拉力要比共轴双旋翼的大。

2)在涵道共轴双旋翼结构中，上旋翼产生的拉力仍然要大于下旋翼所产生的拉力，但当上旋翼逐渐接近涵道唇口时，这一结论会发生逆转。

3)涵道间距的变化会导致上下旋翼拉力和扭矩的变化，这一结论对涵道共轴双旋翼飞行器的设计非常重要。

[1]Allan W R. Axial flow fans and ducts[M]. New York:John Wiley＆Sons Inc，1983.

[2]Kriebel A R. Theoretical investigation of dynamic stability derivative of ducted propellers[J]. Journal of Aircraft，1964，1(4):203－210.

[3]Mendenhall R，Spangler S B，Nielsen Engineering＆ Research，et al. Theoretical study of ducted fan performance，NASA CR －1494[R].1970.

[4]Andrew M J. Co-axial rotor aerodynamics in hover[J].Vertica，1981，5(2):163－172.

[5]Saito S，Azuma A. A numerical approach to co-axial rotor aerodynamics[J]. Vertica，1982，6(4):253 －266.

[6]Bagai A，Leishman J G. Free-wake analysis of tandem，tilt-rotor and co-axial rotor configurations[J]. Journal of American Helicopter Society，1996，41(3):196－207.

[7]童自力，孙茂.共轴式双旋翼气动特性的计算研究[J].航空学报，1999，20(4):348－350.

[8]许和勇，叶正寅.悬停共轴双旋翼干扰流动数值模拟[J].航空动力学报，2011，26(2):453－457.

[9]Johnson E N，Turbe M A. Modeling，control，and flight testing of a small ducted fan aircraft[EB/OL]. [2012 －2－ 08]. Http://www.ae.gatech. edu/people/ejohnson/GTSpyDraft. pdf.

[10]许和勇，叶正寅.涵道螺旋桨与孤立螺旋桨气动特性的数值模拟对比[J].航空动力学报，2011，26(12):2820－2825.