一种基于驾驶决策的三相交通流仿真模型

王 涛，沈益民

(1.滁州学院，安徽 滁州 239000; 2.成都工业学院，四川 成都 611730)

一种基于驾驶决策的三相交通流仿真模型

王 涛1，沈益民2

(1.滁州学院，安徽 滁州 239000; 2.成都工业学院，四川 成都 611730)

提出了一种基于三相交通流理论的驾驶决策交通流仿真模型。该模型采用驾驶决策函数替代由Kerner等人提出的KKW模型中目标速度函数,在新模型中将驾驶行为分为自由流驾驶模式、同步流驾驶模式和堵塞流驾驶模式，三种模式会根据道路的实际交通情况进行切换。基本图和时空分析结果表明，提出的模型符合实际的交通观察。

三相交通流;驾驶决策;交通仿真模型

对交通流相变规律的研究是交通流理论[1-3]的重要研究内容，相变理论中最具有代表性的是Helbing等人的基本图理论[4-5]和Kerner等人的三相交通流理论[6]。由于该问题过于复杂，难以用简单的数学模型描述，常借助于微观交通仿真模型来进行分析，其中由Cremer和Ludwing提出元胞自动机模型是常用的一种分析方法[7]。

上世纪90年代自Nagel和Schreckenberg提出NS模型[8]以来，元胞自动机交通流模型得到了迅猛发展，一系列经典的重要模型[9-13]也相继被提出，包括Kerner等人为研究三相交通流理论而提出的KKW仿真模型[14]。

通过深入分析，本文认为在KKW模型中，当前车辆行驶速度的改变并未考虑到车辆之间的相互制约条件，仅通过孤立的车辆运动假设不能准确地反映车辆流的运动规律。

分析车辆流中车辆相互制约和影响之后，通过分析驾驶员驾驶行为的改变，可以有助于更加细致地描述车流的整体面貌和单个车辆的运动规律，这种改变抽象到数学模型上就是多约束条件下的驾驶函数，用于定量描述车辆的运动规律，便于对交通流进行总体分析。

另外，在KKW仿真模型以及其它众多仿真模型中，仅考虑了前车对后车的影响，但后车鸣笛时对前车的影响很少有文献进行分析。本文综合考虑了以上这些因素，提出了一种新的基于驾驶员驾驶决策的单车道元胞自动机仿真模型，并对该仿真模型进行了拟合验证。

1 驾驶决策模型

图1(a)为三相交通流假说模型的示意图，图1(b)是NGSIM实测数据[15]对该假说模型的拟合验证。通过拟合的效果可以看到，三相交通流模型更加符合交通实测，能明显反映处于自由流区和堵塞区之间的同步流区域。

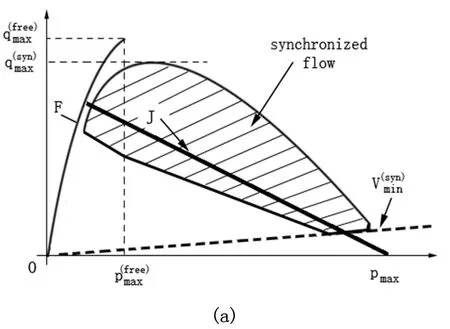
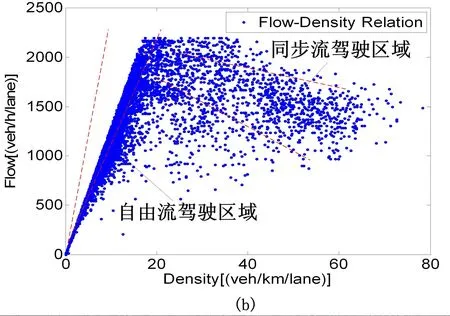
图1 (a)为Kerner三相交通流理论的假说示意图;(b)为基于US101 Highway高速路的实测数据的拟合分析图

在本文的新模型中，每一演化时步被分为两个子步进行，在第一子步，首先判断当前车辆是在自由流区、同步流区或者堵塞区，并根据函数Fc{ηn(t),Pchange}完成驾驶模式的变换；第二子步，车辆在仿真道路的元胞空间内按单车道的更新规则完成车辆演化。

1.1数学模型

仿真模型的驾驶决策函数表示为如式(1)所示的形式：

ηn(t+1)=Fc{ηn(t),Pchange}

(1)

其中第t时刻可能的驾驶模式ηn(t)如式(2)所示：

(2)

则驾驶决策函数Fc{ηn(t),Pchange}的表达式如式(3)所示：

(3)

由式(3)可知，在t+1时步时，驾驶模式可能产生以下4种改变:

(i)M0→M1，当前车辆的速度大于前导车辆的速度，并且与前车的车头距相对较短时，自由流模式的车辆会改为同步流驾驶模式。

(ii)M1→M2，当前车辆的速度大于前导车辆的速度，并且与前车的车头距相对较短时，同步流驾驶模式的车辆会改为堵塞流驾驶模式。

(iii)M2→M1，当前车辆与前车的车头距相对较长时，或者同时由于后车的鸣笛催促，堵塞流模式的车辆会改为同步流驾驶模式。

(iv)M1→M0，当前车辆与前车的车头距相对较长时，或者同时由于后车的鸣笛催促，同步驾驶模式的车辆会改为自由流驾驶模式。

假设驾驶模式M0,M1,M2之间是一阶改变，不存在二阶改变，不存在直接从M0到M2的驾驶模式的改变。驾驶模式的改变概率为Pchange。在定义了驾驶员的驾驶决策过程以后，以下是对每一种驾驶模式更新规则的说明。

1.1.1 自由流驾驶模式

在自由流驾驶模式M0下，车辆演化规则如下所示：

(i)考虑与前车的车头距的加速过程，如果与前车的车头距足够大，即dn(t)>Vmax，则车辆在下一秒以Pmax的概率直接加速到最高速度Vmax，或者以1-Pmax的概率直接加速到Vmax-1。如果与前车的车头距dn(t)≤Vmax，则车辆在下一秒以dn(t)行驶， 规则表示如下：

Vn(t+1)=

(ii)考虑后车鸣笛的加速过程，如果车辆听到了上一时步的后车鸣笛，则以概率Pl按当前速度再加1，规则表示如下：

ifHn-1(t)=1 then

Vn(t+1)=min[Vn(t+1)+1,Vmax],withPl.

(iii)自由流驾驶模式时判断下一时步是否鸣笛，规则表示如下：

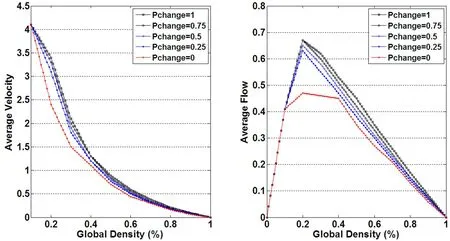
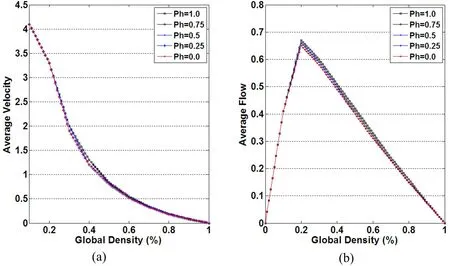
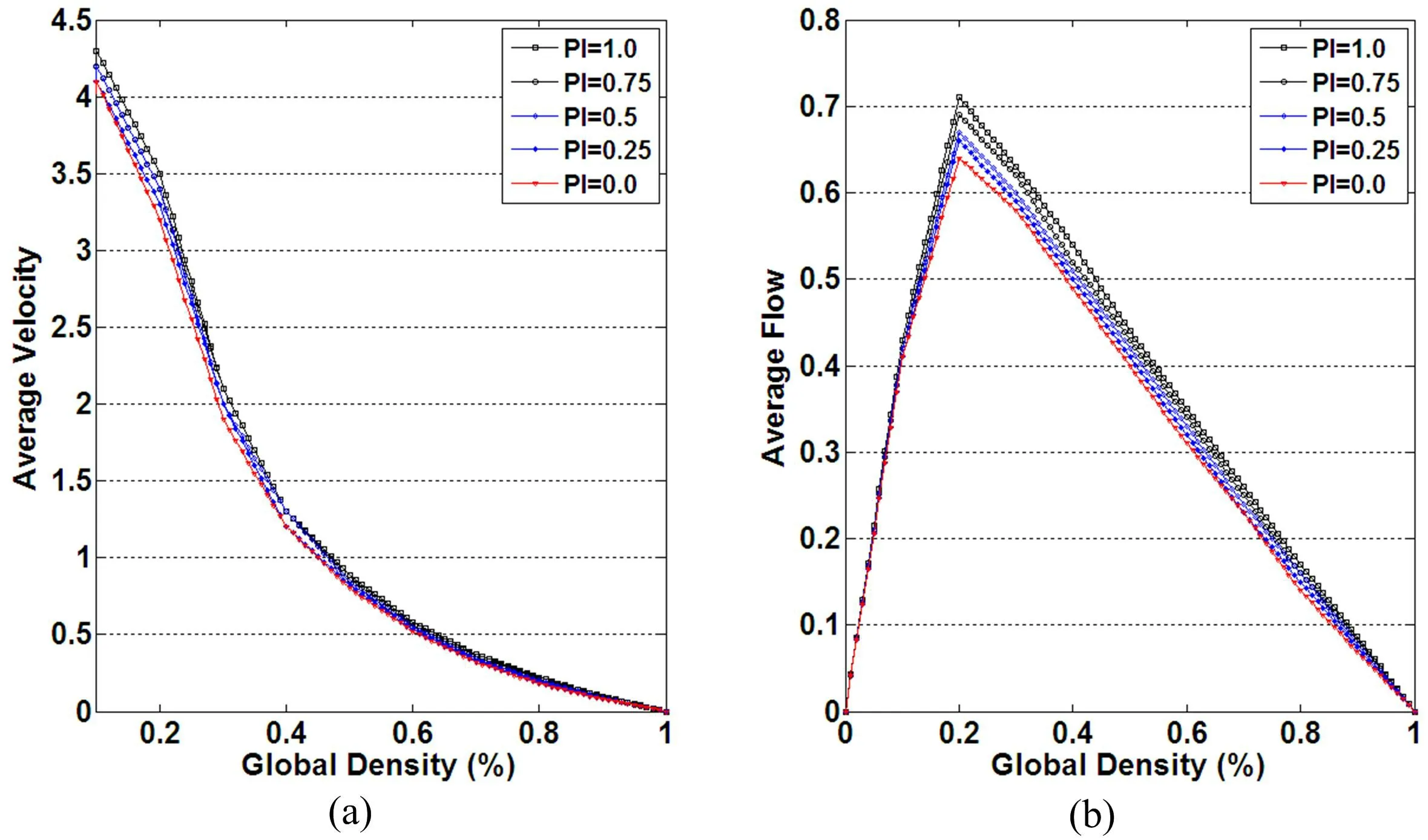
if (dn(t)

Hn(t+1)=1,withPh

else

Hn(t+1)=0.

(iv) 在自由流驾驶模式下，只有当车辆的速度达到最大行车速度Vmax时才执行车辆随机慢化，规则表示如下：

ifVn(t+1)=Vmaxthen

Vn(t+1)=max[Vn(t+1)-1,0]withPsafe

(v)安全减速，规则表示为：

Vn(t+1)=min[Vn(t+1),dn(t)]

(vi)位移，在仿真模型中指车辆前进的元胞数量，表示为：

Xn(t+1)=Xn(t)+Vn(t+1)

1.1.2 同步流驾驶模式

在同步流驾驶模式M1下，车辆演化规则表示成所示5种情况：

(i)如果车头距足够大即dn>Vmax时，则车辆以1-Pmax的概率加速到Vmax-1；如果dn≤Vmax，则车辆根据前车的速度调节本车的速度，如果本车速度大于前车速度，则速度调整为与前车相同；如果本车速度小于前车速度，则速度加1行驶。

Vn(t+1)=

(ii)考虑后车鸣笛的加速过程，如果车辆听到了上一时步的后车鸣笛，则以概率 按当前速度再加1。

ifHn-1(t)=1 then

Vn(t+1)=min[Vn(t+1)+1,Vmax],withPl.

(iii)随机延迟的概率进行一次随机减速操作

Vn(t+1)=max[Vn(t+1)-1,0]withPsafe.

(iv)安全减速

Vn(t+1)=min[Vmax,Vn(t+1),dn(t)]

(v)位移

Xn(t+1)=Xn(t)+Vn(t+1)

1.1.3 同步流驾驶模式

在堵塞流驾驶模式M2下，车辆演化规则表示成如下5种形式：

(i)驾驶员逐步加速，速度加1

Vn(t+1)=min[Vn(t)+1,Vmax]

(ii)考虑后车鸣笛的加速过程，如果车辆听到了上一时步的后车鸣笛，但是车辆将不再以概率Pl加速。

(iii)随机延迟，Psafe的概率进行随机减速操作

Vn(t+1)=max[Vn(t+1)-1,0],withPsafe

(iv)安全减速

Vn(t+1)=min[Vmax,Vn(t+1),dn(t)]

(v)位移

Xn(t+1)=Xn(t)+Vn(t+1).

1.2仿真模型数值实验分析

将仿真空间定义在了一条由格子链组成的一维元胞空间上。该格子链的长度为1000，每一个元胞的长度被规定为7.5m，则道路的长度为

L=1000sites≈7.5km

(4)

在仿真模型中每一个时步对应现实世界的1s，元胞空间中的车辆每次可移动的范围0 cell/s到5 cell/s，所以仿真系统中的最大速度可以表示为

Vmax=5 cell/s≈135km/h

(5)

在初始条件下车辆被均匀的分配在道路元空间上，道路空间中的车辆总数为N，道路长度为L，则在完成共t个时步的演化以后，仿真系统的道路交通流量J、道路平均速度Vavg以及道路平均密度ρ的定义如下：

(6)

(7)

J=ρ×Vavg(veh/s)

(8)

为了保证仿真模型的自完备性，在仿真模型中采用周期式边界条件，每一时步的仿真完成以后都要进行边界检查，让离开系统的车辆重新从仿真元胞空间的头部重新进入系统。

1.2.1 模型基本图分析

取Pchange=0.5、Ph=0.3、Pl=0.3、Pmax=0.25、Psafe=0.15，道路密度的取值范围为0～1.0，仿真系统先运行1000时步达到稳定状态，然后统计1000时步的平均数值特征。

图2当随机性参数取值固定时，在不同的道路密度条件下，仿真系统的基本图分析，其中(a)为平均速度-密度关系图,(b)为平均流量-密度关系图

图2为本模型的流量-密度和速度-密度分析图。可以看出，当道路密度为ρ=0.2时，系统流量出现拐点，系统的临界密度为ρ=ρc=0.2，此时，逼近真实道路系统中的峰值流量Jmax=0.72(veh/s)；Vc=3.6(cell/s)，与真实道路系统中Vc=97.2(km/h)的情况基本一致。在较高密度区域，如ρ=0.8时，Jmax=0.17(veh/s)，逼近真实道路系统中的峰值流量Jmax=612(veh/h)；Vc=0.22(cell/s)相当于真实道路系统中Vc=5.94(km/h)。在中等密度区域，如ρ=0.4时，Jmax=0.54(veh/s)，真实道路系统中约为Jmax=1944(veh/h)；Vc=1.3(cell/s)，约为真实道路系统中的Vc=35.1(km/h)。

从图2可以看出，随着道路密度的增大，道路的平均行驶速度是呈现出下降的趋势，交通流量也会出现拐点。

1.2.2 时空图分析

在对仿真模型进行数值分析时，要使用时空图查看随时间的变化，车流在道路上的间隔状态，首先分析道路密度ρ=0.17，ρ=0.2，ρ=0.4，以及ρ=0.6时的时空图，如图3所示，图中横轴表示车辆的前进方向，纵轴表示时间的演化时步。

图3当随机性参数固定时，在不同道路密度条件下仿真系统的时空分析图

在图3(a)所示的时空图中，当道路交通处于自由流状态，即道路密度ρ=0.17时，车辆为自由行驶模式，车辆间的相互作用较小，并且只在道路局部发生轻微的车辆聚集现象。图3(b)表示道路密度ρ=0.2时的道路时空图。当道路密度ρ=0.2时，道路交通处于临界密度，此时流量达到最大值，从时空图中可以看出，此时在道路空间的大部分区域处于自由流状态，但在某些局部同步流交通已经开始形成。

图3(c)表示当道路密度ρ=0.4时的时空图。此时道路属于中等密度条件，从时空图中可以看出，此时在道路上会有更多的区域正在出现同步流交通，并且在某些位置同步流开始变为宽运动堵塞，此时道路交通呈现出同步流和宽运动堵塞混合的情形。

图3(d)表示在较高道路密度区域，ρ=0.6时的道路交通时空图。此时由于车辆增加，车辆与车辆之间的相互作用加强，所以在道路上会形成较大面积的同步流交通或堵塞流交通，车辆只在部分区域处于自由驾驶状态。

1.2.3 驾驶决策变化概率对交通流的影响

本节将分析驾驶决策变化概率Pchange在取不同值情况下，对道路交通的影响。在分析中，随机控制参数分别为最大加速概率Pmax=0.5；后车鸣笛概率Ph=0.1，在此Ph取值较小，表示约有10%的驾驶员在拥挤交通下会鸣笛催促前车，同时也表示，在道路交通中发生鸣笛的车辆只是一种随机现象；Pl=0.2表示前车听到后车鸣笛时可能会引起加速的概率，在此分析中如果当前车辆听到后车鸣笛时，与前车的车头距较长，则会有20%的可能性尽量再加速1个元胞，否则就不再加速；车辆随机慢化的概率Psafe=0.2。

当驾驶行为变化概率Pchange分别取值为0、0.25、0.5、0.75、1时，而道路道路密度的取值为0～1.0时，在图4(a)和图4(b)中分别给出了道路的基本流量-密度分析图和速度-密度分析基本图。在图4的分析中，分别分析了当Pchange=0的道路基本分析图以及Pchange>0时的道路基本分析图。

可以看出在Pchange=0时，从自由流到拥挤交通流的临界密度和临界流量均要小于当Pchange>0时的情况。并且在Pchange=0时，在中等密度条件下(道路密度ρ在 0.2～0.6之间时)，仿真系统获得的平均流量和平均行驶速度要远低于Pchange>0的情况。

图4不同的驾驶模式变化概率Pchange条件下仿真系统的基本图分析,其中(a)为平均速度-密度关系图,(b)为基本流量-密度关系图

而当Pchange>0时，在低密度区间内(道路密度ρ在0～0.2之间时)和高密度区间内(道路密度ρ在0.6～1.0之间时)，随着驾驶模式变化概率Pchange的增加，道路交通流量和行驶速度也会有所提高，但不如在中等密度条件下(道路密度ρ在0.2～0.6之间时)变化明显。这说明在低密度区间(即自由流区)，由于相对较长的车头距，驾驶员可以自由驾驶，所以改变驾驶行为对交通的影响并不非常明显；而在高密度区间(堵塞流区或接近堵塞流区)，由于交通流极易从同步流状态发展成为宽运动堵塞状态，或者交通流本身就处于宽运动堵塞状态，此时留给驾驶员进行驾驶行为改变的空间并不是很大，而在同步流时适当的改变驾驶模式则可以显著提高道路的交通流量和行驶速度。

1.2.4 鸣笛效应对交通流的影响

在针对后车的鸣笛概率Ph和前车的鸣笛加速概率Pl的分析中，驾驶模式变化概率Pchange的取值为Pchange=0.5，最大加速概率Pmax=0.5，车辆随机慢化的概率Psafe=0.2，道路密度取值范围为0～1.0，则后车的鸣笛概率Ph在不同的取值条件下，道路的交通流量-道路密度基本分析图和行车速度-道路密度基本分析图如图5所示；前车的鸣笛加速概率 在不同的取值条件下，道路的交通流量-道路密度基本分析图如图6所示。

图5不同的鸣笛概率Ph下的交通基本图,其中(a)为平均速度-密度关系基本图,(b)为平均流量-密度关系基本图

从图5和图6的分析结果可以看出，在道路密度ρ<0.2的自由流驾驶条件下，当后车的鸣笛概率Ph取值增加时，交通流的变化不会特别明显，前车的鸣笛加速概率Pl在增加时，道路的交通流量和行车速度会有所增加，本文提出的DDM仿真模型能客观地再现这一交通情形，Ph和Pl在道路密度ρ>0.2的拥挤流条件下，也得到了类似的数值实验结果。

模型中引入的后车鸣笛概率Ph和前车鸣笛加速概率Pl描述一种偶然的鸣笛现象及其对交通流的影响。在自由流条件下或者拥挤流条件下，当后车鸣笛且前车在听到鸣笛后做出反应时，会少量提高道路的交通流量或行驶速度。

图6不同的鸣笛加速概率Pl下的仿真系统基本图，其中(a)为平均速度-密度关系图,(b)为平均流量-密度关系图

同时说明了后车鸣笛概率Ph和前车鸣笛加速概率Pl，只能反映驾驶员期望获得尽量快的行车速度的一种期望，但否能实现加速要依赖于与前车的相对位移。

2 结束语

本文基于Kerner等人提出的三相交通流理论，建立了一种新的基于驾驶决策的机动车流微观仿真模型，为了适当简化问题，模型放在单车道的条件下进行分析，通过添加换道规则、红灯时的停车线减速等规则可以使模型更加具有适应性，在文中对仿真模型进行了数值分析，通过分析可以证明本文所提出的模型可以有效地对交通流状态进行仿真模拟。

[1] 吴建军, 高自友,孙会君,等.城市交通系统复杂性——复杂网络方法及其应用[M].北京：科学出版社，2010：110-114.

[2] 王涛，王俊峰，罗积玉，等.基于时空分析的复杂交通流数据挖掘算法[J].四川大学学报：工程科学版, 2011,43(5):905-909.

[3] 王涛，李志蜀，曾华燊.基于精确传感网络ITS系统的交通流模型研究[J].计算机应用，2012,32(4):905-909.

[4] Schonhof M, Helbing D.Criticism of three-phase traffic theory[J].Transportation Research Part B Methodological, 2009,43(7):784-797.

[5] Schonhof M, Helbing D. Empirical features of congested traffic states and their implications for traffic modeling[J].Transportation Science,2007,41(2):135-166.

[6] Kerner B S, Klenov S L, Wolf D E. Cellular automata approach to three-phase traffic theory[J].J Phys A, 2002, 35:9971-10013.

[7] Cremer M, Ludwig J. A fast simulation model for traffic flow on the basis of Bollean operations[J].J Math Comp.Simul, 1986(28):297-303.

[8] Nagel K, Schreckenberg M. A cellular automaton model for free way traffic[J].J Phys I(France),1992(2) :2221-2229.

[9] Wang T，Wang J F. An adaptive EBCA model probing the problem of riding against the traffic flow[J].Int J Mod Phys C，2011, 22(2): 191-208.

[10] Lan S Y, L Y G, Liu B B. Effect of scopes in highway on traffic flow[J].International Journal of Modern Physics C, 2011，22(4):319-331.

[11] Li X B, Wu Q S, J R. Cellular automaton model considering the velocity effect of a car on the successive car[J].Phys Rev E，2001,066128.

[12] Kerner B S. Cellular automata approach to three-phasetraffic theory[J].J Phys A,2002,35:9971-10013.

[13] Knospe W. A realistic two-lane traffic model for highway traffic[J].Phys A，2002,35: 3369-3388.

[14] Kerner B S, Klenov S L. Microscopic theory of spatial-temporal congested traffic patterns at highway bottlenecks[J].Physical Review E, 2003, 68:036130.

[15] U S Dept. Transp.NGSIM-next generation simulation platform [EB/OL].http://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm.

(责任编辑：张凯兵)

AThree-phaseTrafficFlowSimulationModelBasedonDrivingDecision-Making

Wang Tao1, Shen Yimin2

(1.ChuzhouUniversity,Chuzhou,Anhui239000,China; 2.ChengduTechnologicalUniversity,Chengdu,Sichuan611730,China)

This paper presents a new driving decision-making simulaton model based upon three-phase traffic flow theory by means of improving the KKW model. In the new model, the destination velocity used in the KKW model is substituted by the driving decision-making function and three driving modes are proposed, namely the free flow driving mode, the synchronization driving mode and the jam driving mode which can switch into each other according to the actual traffic conditions. Numerical analysis indicates that the new model is in compliance with the observations of authentic transportation.

three-phase traffic flow theory; driving decision-making; traffic simulation model

TN927

A

2095-4824(2013)06-0005-06

2013-09-17

四川省科技厅应用基础计划项目(2013JY0059)；滁州学院科研启动项目(2012qd07)

王 涛(1979- )，男，山东淄博人，滁州学院计算机学院教师，博士。

沈益民(1968- )，男，四川成都人，成都工业学院教授，博士。