具有极值hyper-Wiener指标的多联苯链

张艳玲 陈香莲 马志辉

（1.昌吉学院数学系 新疆 昌吉 831100;2.石河子大学理学院数学系 新疆 石河子 832003）

1 引言

设G=(V,E)是一个简单，无向连通图，V(G)和E(G)分别是它的点集和边集，图G中u和v之间的距离d(u,v)是G中连接u、v的最短路的边数[1]。G的Wiener指标记为W(G)，定义如下：

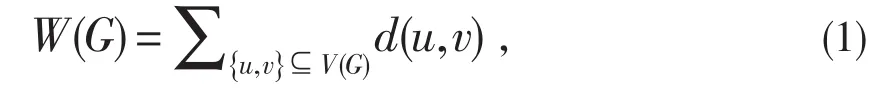
图的hyper-Wiener指标被定义为

多联苯链[3]是由n个苯环B1,B2,…,Bn组成的，其中对任意的正整数k和 j(1≤k＜j≤n)，当且仅当 j=k+1时，Bk和Bj才由一条割边联接，且每一个苯环和一个割边的公共顶点是三度点。

显然，“多联苯链”可以看作是一类重要的线性的无分支的简单的聚苯分子结构图的代表。

图1 三种非同构的联接方式

用Ωn表示包含n个苯环的多联苯链的集合。设Gn∈Ωn，Gn-1∈Ωn-1，Gn能够由Gn-1在其终端由一条割边再联接一个苯环得到，其中n≥2。如果B1,B2,…,Bn是Gn中的n个苯环，我们记Gn=B1B2…Bn，其中Bi和Bi+1是邻接的(i=1,2,···,n-1)。如图1所示，每个在链中的苯环可联接位有五个，但只有三个不同构的联接方式Gn-1→［Gn-1］k=Gn，其中k=1，2，3，我们把这3种不同的粘结方式称为：way-1，way-2，way-3。

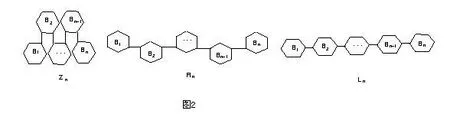
特别地，在多联苯链中每个苯环都可以以一样的联接方式进行联接，如图2。如果多联苯链Gn中的每个苯环都是以“way-1(way-2或way-3)”通过一条割边联接在前一个苯环上的，则记作Zn(Rn或Ln)。

若Gn是一个多联苯链，类似于文献［3］，记［Gn］k是由多联苯链Gn通过way-k(k∈{1,2,3})联接一个新的苯环得到的多联苯链，显然，每个Gn(n≥2)能被写为，其中 kj∈{1,2,3}，则 Gn可简记为：Gn=3k2k3…kn-1(约定L2的代码为3)。对于Gn，若每个kj=1，则Gn=Zn；若每个kj=2，则Gn=Rn；若每个 kj=3，则Gn=Ln。易见

2 主要结果

本文主要研究多联苯链的hyper-Wiener指标，并得到了Zn，Ln分别具有多联苯链Gn的最小、最大hyper-Wiener指标。

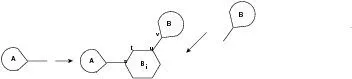
图3 Gn(i,k)

文［3］定义Gn(i,k)(k=1,2,3)如下（见图3）。设 A∈Ωi-1，B∈Ωn-i且Bi是Gn中的第i个苯环，Bi联接A所得的多联苯链记为Gi，B通过way-k(k∈{1,2,3})联接到Gi的最后一个苯环Bi所得的多联苯链记作Gn(i,k)。

为了得到多联苯链的hyper-Wiene指标，先介绍几个引理。

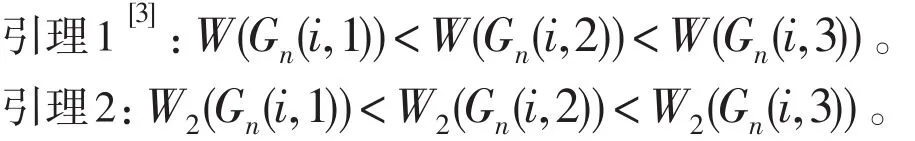
证明：对于任意的Gn(i,k)∈Ωn，由公式（2）可以得到：

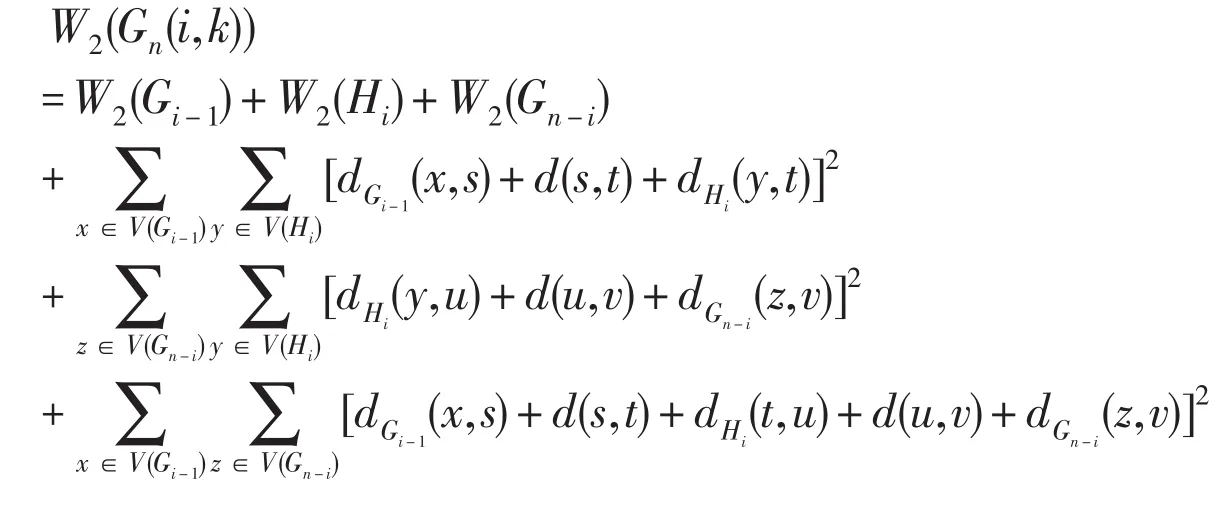
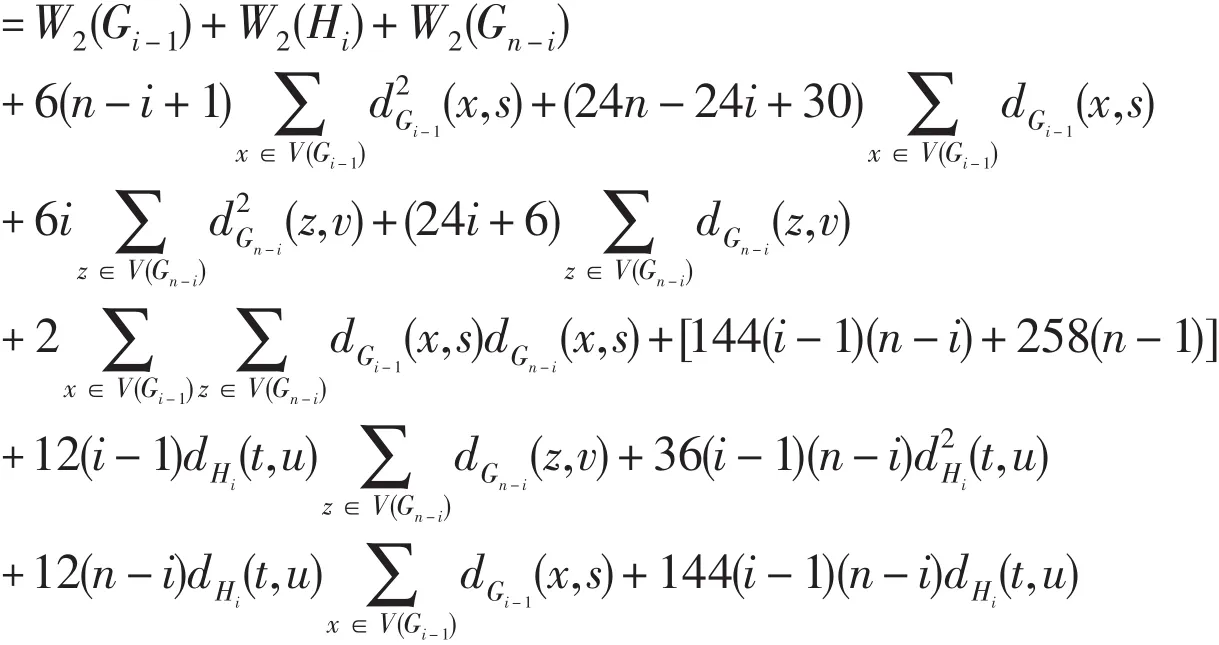
由于

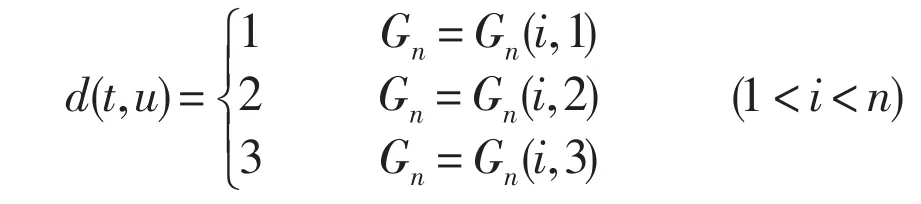
因此有：

由引理1，引理2和（2）式，易得下面引理：

引理3：WW(Gn(i,1))＜WW(Gn(i,2))＜WW(Gn(i,3))

现在，我们给出主要结果及其证明。

定理1：设n为任意正整数且Zn,Ln和Gn∈Ωn，则

(1)WW(Zn)≤WW(Gn)，等号成立当且仅当Gn=Zn。

(2)WW(Gn)≤WW(Ln)，等号成立当且仅当Gn=Ln。

证明：我们通过反证法证明定理1。

情况1.若ki=2,即，由 引 理 3,这与Gn具有最小hyper-Wiener指标矛盾，故Gn=Zn。

情况2.若ki=3，用证明情况1的方法类似可证。

(2)用类似（1）的方法可以证明WW(Gn)≤WW(Ln)。

［1］Bondy JA,Murty USR.Graph theory with applications［M］.New York:The Macmillan Press,1976.

［2］罗朝阳等.具有极值的Wiener和hyper-Wiener指标的六环螺链［J］.山东大学学报，2010，45（12）:16-21.

［3］X.Gu,B.Zhao,J.Tang,Polyphenyl Chains with Extremal Wiener Index［J］.新疆大学学报，2010，27（1）：32-36.

［4］X.Chen,B.Zhao,P.zhao,Six-membered ring spiro chains with extremal Merrifield-Simmons index and Hosoya index,MATH.Commun.Math.Comput.Chem.62(3)(2009)657-665.