网络效率优化视角下的集群最优创新合作绩效

黄玮强，姚 爽，庄新田

1东北大学 工商管理学院，沈阳110819

2沈阳化工大学 经济与管理学院，沈阳110142

1 引言

产业集群(以下简称集群)创新系统是由集群主体、关系和属性组成的复杂系统［1］，随着创新活动中所需知识、技能及资源的复杂化和多元化发展，集群主体之间建立了各种正式或非正式的创新合作关系［2］，集群创新合作网络是对集群主体之间复杂创新合作关系的形象化描述。

集群创新合作网络的拓扑结构会影响集群内部的知识流动和扩散［3］，依赖于创新合作关系的集群主体间的知识流动和扩散影响集群的创新合作绩效，较高的集群创新合作绩效说明集群创新合作网络(特别是特定的网络结构)具有较高的效率。因此，挖掘集群创新合作网络结构形成的动力学过程，有利于理解集群的知识流动和创新机制。本研究通过对比分析稳定状态网络与最优效率网络的拓扑结构特征差异，探讨集群的自组织创新合作绩效如何、是否达到最优，从合作网络拓扑结构角度剖析集群自组织创新合作绩效未达到最优的原因，进而提出相应的提升绩效的政策建议。

2 相关研究评述

Jackson等［4］引入网络稳定性和效率的概念，采用博弈论方法分析经济网络的内生形成过程;之后学者们将研究范围拓展至随机稳定网络［5］以及企业R＆D合作网络［6-7］。上述研究得到的均是对称情形下的均衡网络，如环形网络、全连接网络、星形网络或空网络，这些网络的拓扑结构特征完全不同于现实的社会或经济网络。大量的实证研究发现集群创新合作网络具有普遍相似的拓扑结构特征，如上海世博会旅游产业集群［8］、中关村产业集群［9］、杭州手机产业集群内的企业网络［10］以及德国慕尼黑和英国剑桥生物技术产业集群的职业联系网络［11］均具备小世界网络的拓扑结构性质，即网络具有较短的平均路径长度和较大的平均聚集系数。

以上研究主要关注两个核心问题［12］。一方面，当网络个体通过选择不同的网络联系伙伴来最大化自身收益时，最终会形成什么样的网络(稳定网络);另一方面，网络个体自利选择所形成的网络的效率如何。为了得到与实际社会网络的拓扑结构特征相 一 致 的 稳 定 网 络，Carayol等［13-14］和 Jackson等［15］通过引入网络个体的不同空间位置以及网络直接连接的空间成本，改进个体的收益函数，研究结果表明，在较大的参数取值范围内，动态演化形成的稳定网络具有小世界特征;田钢等［16］从集群主体与外部环境互动关系的视角出发，建立集群创新网络的演化动力仿真模型，并以中关村海淀园创新网络为例进行模型验证;黄玮强等［17］研究企业创新网络的自组织演化模型。尽管已有研究得出的稳定网络拓扑结构特征接近于实际网络，但无论从解析角度还是数值计算角度均很难判定稳定网络在多大程度上有效率、它们是否与最优效率网络具有结构上的差异［18］。Carayol等［19］提出利用遗传算法计算最优效率网络，将该方法运用于已有的一些简单模型中(包括Jackson等［4］提出的模型，其对应的最优效率网络是已知的)，研究结果表明，该方法可以稳健地、准确地计算出这些模型对应的最优效率网络。

与已有研究不同，本研究考虑以下两个方面。①在创新合作的知识溢出背景下，将集群主体置于知识空间中，主体间的知识水平差异是影响创新合作成本的重要因素;②由于集群主体的空间聚集性，主体间的空间位置距离对于创新合作成本的影响可以忽略不计。

3 集群创新合作网络基本概念及创新合作过程

利用网络节点和连边分别表示集群主体及它们之间的创新合作关系，集群主体的数量为 n，节点集合记为 N，N={1，2，…，n}，n≥3，任意节点 i与节点 j之间的连边记为ij，若将集群创新合作网络记为g，那么ij∈g。创新合作关系的建立是集群主体i和j的共同决策，因而连边ij是无向边，网络g是无向网络。

3.1 基本概念

分别用gN和gφ表示完全连接网络和空网络，完全连接网络指网络中任意两个节点间均存在连边，空网络指网络中所有节点都是孤立点。在网络g的基础上通过增加连边ij形成的网络记为g'，g'=g+ij=g∪{ij}。在网络g的基础上删除连边ij形成的网络记为 g″，g″=g-ij=g{ij}。网络 g 与g'、g 与g″是相邻网络。在网络g中，与节点i直接相连的节点集合记为Ni(g)，ηi(g)为该集合中的节点数量，即为节点i的度，η(g)为网络的连边数量。在非空网络g中，由任意节点i出发到达任意节点j需要经历一些网络连边，这些连边所构成的集合即为两节点间的一条路径，该边集中所包含的边数即为路径的长度，节点i与j之间的所有路径形成的集合记为i↕gj。集群主体 i与 j的合作关系距离dg(i，j)可定义为节点i与j的最短路径长度，若节点i与 j之间不存在连通的路径，则令dg(i，j)= ∞ 。

3.2 创新合作过程

假设集群主体完成某项创新需要两类知识，分别记为 x和y，主体i所具备的知识可表示为ki，ki=［ki，x，ki，y］，i=1，2，…，n。集群主体 i在知识空间 Ω 中的坐标位置 (xi，yi)，依赖于其拥有的知识禀赋 ki，x和ki，y，即 有xi=ki，x，yi=ki，y。

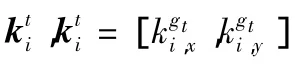
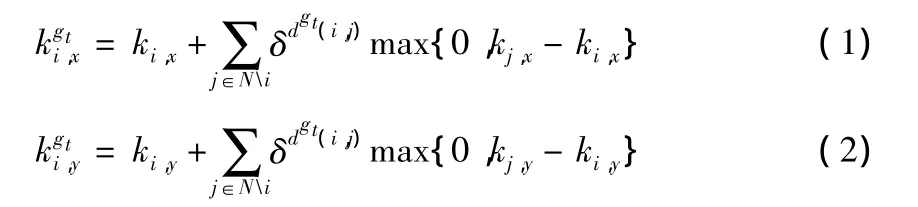
其中，δ为集群主体间知识溢出的效率，0≤δ≤1;dgt(i，j)为节点i与节点j的合作关系距离。如果合作关系距离逐渐增大，合作一方从另一方获取的知识溢出呈指数递减，且δ越小递减得越快。特别地，当集群主体i与j不存在任何直接或间接创新合作关系时，即dg(i，j)=∞，前者无法从后者那里获取知识溢出。

基于创新合作活动的知识溢出受知识接收方的吸收能力影响，而知识吸收能力又与企业的研发投入和社会能力(如基础设施、财务系统、人才市场)密切相关，企业间的知识溢出还受知识本身性质(如编码知识或沉默知识、知识异质性、知识的粘性)以及集群环境等的影响。因此，知识溢出效率参数综合反映了上述各因素对知识溢出的影响。经过大量实证检验的最著名的两个知识生产函数为Griliches-Jaffe知识生产函数［20］和 Romer-Jones知识生产函数［21］，这两个知识生产函数均采用柯布 -道格拉斯生产函数形式。

根据上述的知识生产函数建模原理，集群主体i在［t，t+1］时期的创新收入为

在同一时期，集群主体i的创新合作成本Cgti为

其中，c0为集群主体内部成本，dΩ(i，j)为主体i与j在知识空间中的知识距离(差异)，c为单位知识距离成本 系 数。Carayol 等［13-14］、Jackson 等［15］和 黄 玮 强等［17］将企业间的空间位置距离视为影响创新合作成本的重要因素。与之不同的是，由于集群主体的空间聚集性，主体间的空间位置距离对于创新合作成本的影响可以忽略不计。合作双方知识水平差异越大，双方需要支付更多的费用，如人员培训和技术沟通等，进而增加合作成本。运用欧氏距离衡量两个集群主体在知识空间中的距离，即

其中，dΩ(i，j)表示集群主体i与j的综合知识水平差异。综上，集群主体i在［t，t+1］时期的创新收益为

4 稳定状态网络的自组织演化过程

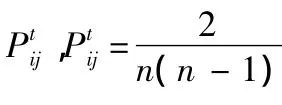
(2)记g't=gt+ij=gt∪ {ij}、g″t=gt-ij=gt{ij}。给定时期 t选中的节点对ij，若ij∈gt，当且仅当≥和≥同时成立时，主体i和j继续维持他们的合作关系，为主体 i在网络g″t中的创新收益，为主体 j在网络g″t中的创新收益;若ij∉gt，当且仅当≥和≥同时成立且其中至少一个是严格不等式时，主体i与j新建合作关系，为主体i在网络g't中的创新收益，为主体j在网络g't中的创新收益。

(4)令t=t+1，循环执行步骤(1)～步骤(3)。

5 基于遗传算法的最优效率网络

在创新合作网络gt中，所有集群主体的创新收益总和S(gt)反映该网络的效率，即

根据 Jackson等［4］提出的最优效率网络概念，在创新合作网络gt中，若集群主体的创新收益总和达到最大，则称网络gt为最优效率网络，即对于所有的网络g⊆gN有S(gt)≥S(g)。值得注意的是，在不同的网络下集群主体的创新收益总和可能同时达到最大，即最优效率网络可能并不唯一。最优效率网络的计算问题本质上就是在众多的潜在创新合作网络中，找出一个(若干个)网络使集群主体的创新收益总和(同时)达到最大，然而无论从解析角度还是传统的数值角度计算最优效率网络都十分困难。借鉴Carayol等［19］的研究，根据遗传算法原理设计最优效率网络的优化过程。基于遗传算法的网络优化计算步骤如下。

(2)群体初始化。在进化的初始时刻(T=0)，选取m个长度为L的个体(0-1二值数串)，个体中的数值随机给定，形成规模为m的初始群体。

(3)选择。记进化时期T的群体为P(T)，P(T)={Bq}T，q=1，2，…，m，T=0，1，…，Tmax，Tmax为 进 化 代数。根据(7)式分别计算T代的m个个体对应的适应度，m个适应度的平均值为 Πaverage、最大值为 Πmax，记与Πmax相对应的个体为Bmax，运用轮盘选种法［23］，从T代群体中选择m个个体作为参与下一代群体进化的父代个体。

图1 合作网络的0-1二值数串表示方法Figure 1 Representation of 0-1 in Collaboration Performance

(4)杂交。设定杂交概率为pcross，首先随机选取两个通过选择算法得到的父代个体，然后运用两点杂交算子［23］产生后代个体。重复以上步骤，直到m·pcross个父代个体都完成了杂交操作，通过杂交形成了子代个体。

(5)突变。设定突变概率为pmut，由杂交产生的子代个体所有位串产生突变的几率为m·L·pmut。具体步骤为，随机从m个子代个体中选取一个个体，然后随机选取该个体中的某个位置，完成数值变换(即由1改为0或由0改为1)。重复上述的选取变换过程，直到m·L·pmut个位置都完成了数值变换。

(6)经过杂交和突变操作后形成的m个子代个体成为进化时期(T+1)的新群体。循环执行步骤(3)～步骤(5)。

(7)若最近连续的5代群体中每代群体的平均适应度和最大适应度的平均差异小于ε(ε为根据许可精度设定的某个极小阈值)，则优化过程停止，由此搜寻到最后一代中的最优个体Bmax，与Bmax对应的创新合作网络即为最优效率网络。

6 创新合作网络的拓扑结构指标

(1)平均路径长度

网络的平均路径长度为d，反映了任意两节点间的平均合作关系距离，平均路径长度越小，说明集群主体间实现创新合作需要经历的中介主体数量越少。

(2)平均聚集系数

网络的平均聚集系数为C，表示某集群主体的合作伙伴间也互为合作伙伴的可能性［18］。该指标从本质上反映了集群主体之间合作关系的紧密程度，即

其中，#{·}为集合基数，j和l分别为集群主体i的合作伙伴。

(3)平均度

节点i的度表示与该节点直接相连的其他节点数目。网络的平均度K(所有节点的度的平均值)反映了集群主体的平均合作规模大小，即

与度有关的统计量还包括网络最大度值与最小度值间的差异r、直接相连两节点间的平均度值差异u和网络节点度值的标准差 V。u反映节点度值的非对称程度，V反映度值分布的离散程度。

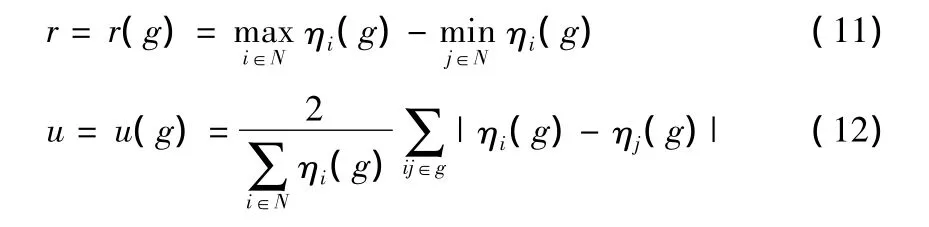
7 稳定状态网络与最优效率网络的比较分析

7.1 仿真参数设计

假设网络规模n=20，集群主体的知识禀赋服从0～ 1 均匀分布，即ki，x～ U［0，1］和ki，y～ U［0，1］。知识溢出效率δ∈(0，1］，以下的仿真计算中将以0.010为参数间隔，取100个不同的δ值。由于δ=0时任何集群主体间均不会建立合作关系，因此不考虑这种参数情况。为了研究参数的变化规律，对集群主体的创新收益函数进行简化，令c0=0和c=0.030。

在网络演化的初始时刻，网络无任何连边，¯ε=0.0001。群体规模m=500，群体中的每个个体用长度为 L 的0-1二值数串表示，n=20。根据 Schaffer［24］关于遗传算法参数设定的建议，杂交概率pcross=0.600，突变概率pmut=0.001。

7.2 网络演化中的连边数量变化

在每个网络演化时期，各集群主体根据创新合作的收益决定是否新建或取消已有的合作关系，主体间合作关系的增减体现为网络连边的增减，进而引起网络的自组织动态演化。图2为随着演化时期的推进不同知识溢出效率水平下合作网络的连边数量变化图，这里列出当 δ值分别为0.100、0.500、0.700和0.900的情形。随着网络的演化，网络连边数量稳定增加，直到某一时期达到最大，之后便保持在一个稳定的水平不变。如当δ=0.100时，在演化时期t≈500左右，网络的连边数量达到最大(约为30)，之后便稳定地保持在该水平。从总体上看，不同知识溢出效率水平下，在网络演化时期t≈1 500之前，合作网络即可自组织演化至稳定状态。

图2 创新网络演化过程中集群主体间合作关系数量变化情况Figure 2 Changes of Collaborative Relationship Number of Cluster Individuals during the Innovation Network Evolution Process

7.3 网络的效率及公平性

图3给出不同δ值下经过遗传算法得到的最优效率网络与自组织演化稳定状态网络的效率对比情况。由图3可知，随着δ的增大，两个网络的效率随之显著增加，说明提高主体间的知识溢出效率可以有效提升集群的社会福利。此外，还可以看出最优效率网络的效率增加速度要快于稳定状态网络。

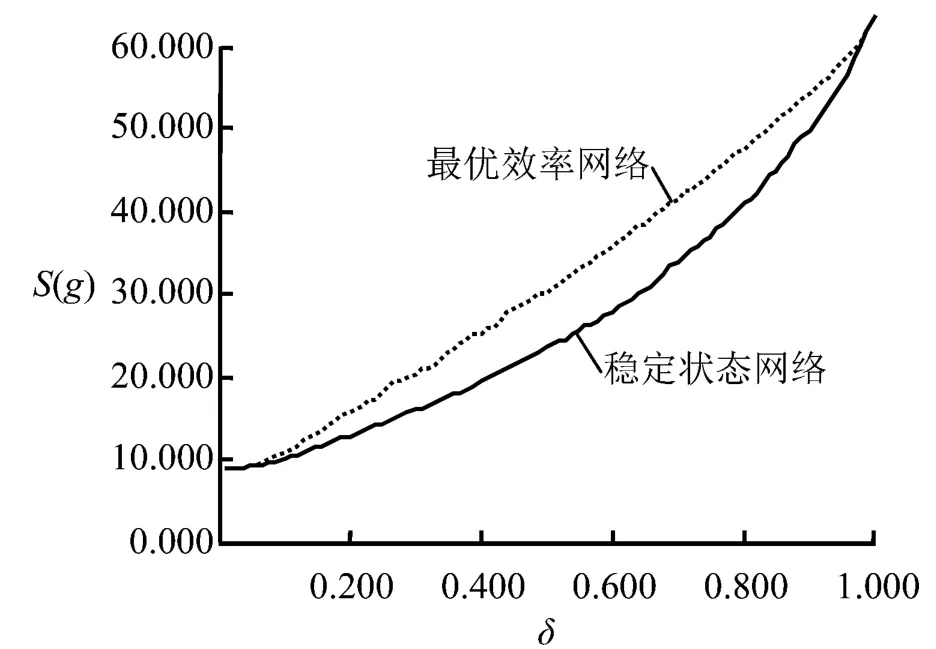
图3 最优效率网络和稳定状态网络的效率变化情况Figure 3 Changes of the Efficiency of Efficient Network and Stable Network

图4给出不同δ值下两种网络的效率差距变化情况，即最优效率网络的效率减去稳定状态网络的效率，用G表示。由图4可知，当δ接近于0或1时，稳定状态网络与最优效率网络的效率差距为0，其他情况下两种网络的效率差距均大于0。特别地，当δ=0.660时两者的效率差距达到最大值8.429，这从另一个侧面验证了遗传算法在搜寻最优效率网络方面的可靠性。当δ处于中等水平时，稳定状态网络的效率有较大的提升空间。稳定状态网络是每个集群主体在最大化其自身收益前提下形成的，它反映了主体的最优选择。但是，每个集群主体的最优选择往往不能带来集群整体的最优效率，这也说明了个体与整体的冲突。

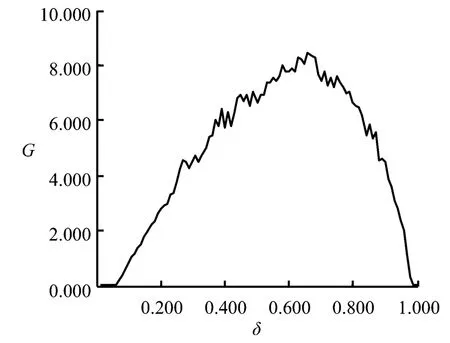
图4 最优效率网络与稳定状态网络的效率差距变化情况Figure 4 Changes of Efficiency Differences of Efficient Network and Stable Network

用集群主体创新收益的标准差SD来衡量网络的资源配置公平性，即

图5 最优效率网络和稳定状态网络的资源配置公平性变化情况Figure 5 Changes of Resource Allocation Fairness of Efficient Network and Stable Network

由图5可知，随着δ的增大，两种网络的集群主体创新收益标准差均呈先减小后增加的变化规律。在稳定状态网络中，当δ=0.370时集群主体创新收益标准差达到最小值0.131;在最优效率网络中，当δ=0.150时创新收益标准差达到最小值0.044。当δ=0.230时两种网络的资源配置公平性几乎相同，最优效率网络为0.154，稳定状态网络为0.152;当δ＜0.230时，最优效率网络的资源配置公平性要高于稳定状态网络;而当δ＞0.230时，稳定状态网络具有较高的资源配置公平性。综合观察图3～图5发现，从总体上看，当δ＞0.230时，要提高集群创新合作网络的效率水平，必须要以牺牲网络的资源配置公平性为代价。但当知识溢出效率较低时(δ＜0.230)，可以同时提高集群创新合作网络的效率和资源配置公平性。

7.4 网络的平均度

图6 最优效率网络和稳定状态网络的平均度变化情况Figure 6 Changes of Average Degree of Efficient Network and Stable Network

图6给出不同δ值下最优效率网络和稳定状态网络的平均度变化情况。由图6可知，随着δ的增大，两种网络的平均度变化曲线均呈倒U形，在δ的取值范围内，稳定状态网络的平均度都小于最优效率网络的平均度。创新合作中的知识溢出使集群主体的直接合作伙伴或者间接合作伙伴均可享受到新建合作关系带来的好处，在这种外部性的驱使下，自利性的集群主体不会考虑整体的社会福利水平，进而导致稳定状态网络中集群主体间的不充分合作。因此，在集群的发展过程中，应通过政策补贴等方式尽量避免集群主体的自利行为，激励他们积极地构建创新合作关系，进而提升集群创新绩效。

7.5 网络的平均路径长度

网络连边数量影响网络的拓扑结构特征，具有较多连边数量的网络会有更小的平均路径长度，因此无法判断网络的较小平均路径长度是由于连边的结构性差异还是仅仅由于具有更多的连边数量造成。由已有分析结论可知，在同一参数条件下(即相同网络规模和知识溢出效率)，最优效率网络与稳定状态网络的平均度(连边数量)差异较大，因此应在去除两种网络的连边数量差异影响之后比较分析它们的拓扑结构特征。具体做法是，对于每个最优效率网络或稳定状态网络，产生1 000个与之具有相同节点数量和平均度(连边数量)的随机网络，计算该1 000个随机网络的平均路径长度等拓扑结构参数的平均值，然后计算最优效率网络或稳定状态网络与同等规模随机网络拓扑结构参数的比值，该比值即是在去除了网络连边数量差异影响之后的修正拓扑结构参数。

图7(a)给出不同δ值下最优效率网络和稳定状态网络的平均路径长度(d)的变化情况。由图7(a)可知，当δ值较小时，稳定状态网络的平均路径长度较小;随着δ增大，网络平均路径长度稳定地保持在2.000～2.500的水平;当δ接近于1时，平均路径长度突破之前的稳定水平而增加至4.000左右。在不同的δ值下，最优效率网络的平均路径长度稳定地保持在1.000～2.000之间。对比两个网络的平均路径长度发现，当δ≤0.040时，稳定状态网络的平均路径长度小于最优效率网络的平均路径长度;当δ＞0.040时，前者大于后者，特别是当δ接近于1时，两种网络的平均路径长度差距变得更大。图7(b)给出不同δ值下最优效率网络和稳定状态网络的修正平均路径长度变化情况，其中drand为1 000个同等规模随机网络的平均路径长度均值。对比两个网络的修正平均路径长度发现，当 δ取值为0.010和0.020及δ∈［0.060，0.110］时，稳定状态网络的平均路径长度小于最优效率网络的平均路径长度;当 δ取其他值时，前者大于后者;当δ接近于1时(0.800≤δ≤0.980)，两种网络的修正平均路径长度差异变得较小。

图7 最优效率网络和稳定状态网络的平均路径长度和修正平均路径长度变化情况Figure 7 Changes of the Average Path Length and the Corrected Average Path Length of Efficient Network and Stable Network

图8 最优效率网络和稳定状态网络的平均聚集系数和修正平均聚集系数变化情况Figure 8 Changes of the Average Clustering Coefficient and the Corrected Average Clustering Coefficient of Efficient Network and Stable Network

综合观察图7(a)和图7(b)发现，当0.140≤δ≤0.770时，两种网络的修正平均路径长度对比情况类似于平均路径长度的对比情况;当δ取其他值时，两个指标得出的结论有所不同，此时网络的连边数量差异影响平均路径长度的对比分析结论。因此，需要通过去除网络的连边数量差异影响，进一步挖掘两种网络本身结构性差异对平均路径长度的影响(如图7(b)所示)。从两种网络的修正平均路径长度对比结果看，绝大多数情况下应通过减小稳定状态网络的平均路径长度并使其接近于最优效率网络，进而实现优化集群创新合作绩效的目标。具体来说，一方面应鼓励知识禀赋差异较大的集群主体间建立创新合作关系，这些高成本的远程合作关系能有效地降低网络的规模;另一方面还应适当提高集群主体间的知识溢出效率，如增强知识接收方的吸收能力、减小知识的粘性和改善集群的合作环境等。

7.6 网络的平均聚集系数

图8(a)给出不同δ值下最优效率网络和稳定状态网络的平均聚集系数(C)变化情况。由图8(a)可知，当δ∈(0.000，0.200)或δ∈(0.600，1.000)时，稳定状态网络的平均聚集系数小于最优效率网络;当δ∈［0.200，0.600］时，两种网络具有大致相同的平均聚集系数。图8(b)给出不同δ值下最优效率网络和稳定状态网络的修正平均聚集系数变化情况，其中Crand为1 000个同等规模随机网络的平均聚集系数均值。由图8(b)可知，除δ接近于0或1时的少数情况外，稳定状态网络的修正平均聚集系数要大于最优效率网络。值得注意的是，当δ接近于1时，稳定状态网络的修正平均聚集系数小于最优效率网络。与此同时，由图7(b)可知稳定状态网络的修正平均路径长度在不断地减小，并向最优效率网络靠拢，图8(a)和图8(b)得出的不同结论表明，稳定状态网络和最优效率网络的连边数量差异会影响网络平均聚集系数。因此，需要通过去除网络的连边数量差异影响，进一步挖掘两种网络本身结构性差异导致的不同聚集性(如图8(b)所示)。

从两种网络的修正平均聚集系数对比结果看，绝大多数情况下应通过减小稳定状态网络的平均聚集系数并使其接近于最优效率网络，进而实现优化集群创新合作绩效的目标。应弱化集群主体对合作伙伴的“偏好性选择”，即偏好于合作关系距离和知识距离小的合作对象。具体地，可以通过广泛和多样化的集群主体交流平台，创造更多的合作机会，使集群主体的创新合作行为跳出已有的小范围关系圈，降低合作的局部聚集性。

7.7 网络的小世界性

Davis等［25］提出小世界性度量指标 SW，即

当SW显著大于1时，可以认为实际网络为小世界网络。图9给出不同δ值下稳定状态网络和最优效率网络的SW值变化情况。

从图9可知，当0.070≤δ≤0.910时稳定状态网络的SW值显著大于1，此时的网络具有小世界性;在不同δ值下最优效率网络的SW接近于1，因为最优效率网络具有与同等规模随机网络相似的平均路径长度和平均聚集系数(图7(b)和图8(b))。众所周知，实际复杂网络普遍具有小世界性特征，上述结论一方面表明稳定状态网络能较真实地反映实际网络的形成演化规律;另一方面说明在实际的创新合作中，集群主体之间的知识溢出效率不会达到极端值，如极端地接近于0或1。最优效率网络所具有的随机网络性质以及稳定状态网络的小世界性，事实上是前述网络平均路径长度和平均聚集系数结论的综合性反映，该结果再次表明，为了优化集群的创新合作绩效，应尽量增强集群主体间创新合作关系的随机性，减小其自组织演化偏差。

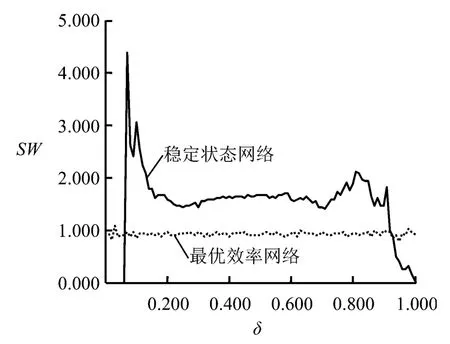
图9 最优效率网络和稳定状态网络的SW值Figure 9 The Quotients(SW)of Efficient Network and Stable Network

7.8 与度有关的网络统计量

图10给出不同δ值下最优效率网络和稳定状态网络的节点度值标准差变化情况。当δ＜0.060时，稳定状态网络的节点度值分布离散程度小于最优效率网络;当0.100≤δ≤0.540时，稳定状态网络的节点度值分布离散程度大于最优效率网络;当δ取其他值时，两种网络的节点度值分布离散程度相近。两种网络的修正节点度值标准差变化情况与图10高度相似，说明网络的连边数量对节点度值分布的离散程度影响不大。当0.060≤δ≤0.540时，稳定状态网络的修正节点度值标准差大于最优效率网络;除δ=0.010外，当δ取其他值时，两种网络的节点度值分布离散程度相近。篇幅所限，不再图示。

图10 最优效率网络和稳定状态网络的节点度值标准差变化情况Figure 10 Changes of the Node Degree Standard Deviation of Efficient Network and Stable Network

图11给出不同δ值下稳定状态网络和最优效率网络的节点最大度与最小度之差变化情况。当δ＜0.060时，稳定状态网络的节点最大度与最小度之差小于最优效率网络;当0.100≤δ＜0.550、0.550＜δ＜0.650时，稳定状态网络的节点最大度与最小度之差大于最优效率网络;当δ取其他值时，两种网络的节点最大度与最小度之差相近。两种网络的修正节点最大度与最小度之差变化情况与图11高度相似，说明网络的连边数量对节点最大度与最小度之差影响不大。篇幅所限，不再图示。

图11 最优效率网络和稳定状态网络的节点最大度与最小度之差变化情况Figure 11 Changes of Gap between the Biggest and Smallest Node Degree of Efficient Network and Stable Network

图12给出两种网络的平均度值差异。当δ＜0.040时，稳定状态网络的平均度值差异小于最优效率网络;当0.060≤ δ＜ 0.660、0.800＜δ＜ 0.870、0.870＜δ≤0.950时，稳定状态网络的平均度值差异大于最优效率网络;当δ取其他值时，两种网络的平均度值差异相近。两种网络的修正平均度值差异变化情况与图12高度相似，说明网络的连边数量对平均度值差异影响不大。篇幅所限，不再图示。

综合上述与度有关的3个修正统计量研究结果发现，当0.040≤δ≤0.650时，稳定状态网络内部节点连接的非均衡性大于最优效率网络，即各集群主体所参与的创新合作数量差异更大，此时应该降低网络节点连接的非均衡性，进而提升网络效率。换句话说，各主体所参与的创新合作数量越平均，越有利于提升集群的创新合作绩效。从总体上看，最优效率网络的节点连接均衡性接近于同等规模的随机网络;而稳定状态网络的节点连接比同等规模随机网络更不均衡，在某些知识溢出效率水平下(如0.040≤δ≤0.100)，前者更是达到了后者的2倍～5倍。

图12 最优效率网络和稳定状态网络的两节点间的平均度值差异变化情况Figure 12 Changes of the Average Degree Gap between Two Nodes of Efficient Network and Stable Network

7.9 集群主体创新合作的知识互补性

若直接合作的集群主体i与j的知识具有互补性，则 满足(ki，x-kj，x)(ki，y-kj，y)＜ 0。图13给出不同 δ值下两种网络中互补性合作关系数量占所有合作关系数量的比例ratio的变化情况。

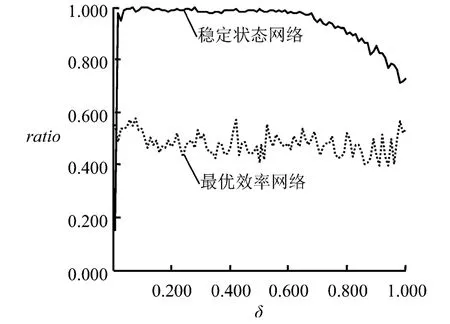
图13 最优效率网络和稳定状态网络集群主体间互补性合作关系数量比例的变化情况Figure 13 Changes of the Complementary Collaboration Number Ratio of the Cluster Individuals of Efficient Network and Stable Network

由图13可知，当0.010＜δ≤0.680时(δ=0.010，绝大部分情况下网络没有连边)，稳定状态网络中知识互补性合作关系数量比例接近于1，说明此时集群主体建立合作关系的前提是知识互补，即各自获取对方的相对优势资源。当δ＞0.680时，随着知识溢出效率的提高，知识互补性合作关系数量比例开始下降，当δ=1.000时降低至0.710左右，说明当知识溢出效率较高时，一些集群主体会与其他在两个知识维度均劣于自身的主体合作。这是因为虽然直接合作没有给知识绝对优势方带来收益，但较高的知识溢出效率会大大提高间接合作的收益，当间接合作收益超过直接合作带来的成本时，这种表面看似“不公平”的合作便产生了。

在不同的δ值下，最优效率网络中的互补性合作关系数量比例稳定地保持在0.400～0.600之间，即互补性合作关系数量与非互补性合作关系数量相当。说明从网络效率优化的角度看，应大力发展集群内部的非互补性合作关系，特别是知识溢出效率水平较低时。具体地，可以向知识绝对优势方提供合作补贴，用于激励其参与非知识互补性创新合作。

8 结论

本研究在集群创新合作网络框架下，建立集群主体的理性创新合作决策模型和合作网络的自组织演化机制，运用数值仿真方法研究网络的动态演化规律和稳定状态网络，运用遗传算法优化计算并得到最优效率网络，从网络效率和公平性、网络基本拓扑结构特征、集群主体创新合作的知识互补性等方面比较分析稳定状态网络和最优效率网络。得出以下研究结论。

(1)集群创新合作网络会自组织演化至稳定状态。从网络总体拓扑结构特征看，在大多数情况下稳定状态网络具有小世界性，最优效率网络更接近于随机网络。

(2)随着知识溢出效率的提高，稳定状态网络与最优效率网络之间的效率差距呈先增大后减小的变化规律。当知识溢出效率超出特定水平时，要提高网络的自组织演化效率必须要以牺牲网络的资源配置公平性为代价。

(3)稳定状态网络的连边数量显著小于最优效率网络。绝大多数情况下稳定状态网络的平均路径长度和平均聚集系数大于最优效率网络，在某些情况下稳定状态网络内部节点连接的非均衡性大于最优效率网络。

(4)集群主体的创新合作需要满足知识互补性条件，即知识溢出效率比较低。虽然非互补性合作关系带来的社会福利大于合作成本，但它给集群主体带来的私人收益却大于合作成本，进而阻碍这种合作关系的建立，此时稳定状态网络的非互补性创新合作关系少于最优效率网络。知识溢出效率的提高导致非互补性合作关系逐渐出现，但总体上看其比例仍然少于最优效率网络。

综上所述，集群主体创新合作的自组织演化存在合作不充分、缺乏高成本的远程合作关系、合作过于局部化、偏好连接下的合作规模非均衡性以及过分依赖知识互补性等问题，这些问题在知识溢出效率较低时尤为明显。为了提高集群创新合作绩效，集群发展的政策制定者应纠正上述自组织演化偏差。具体地，可以通过政策补贴的方式，弥补个别集群主体的私人损失，激励他们参与到有利于提升集群整体创新合作绩效的创新合作中。当然，这种非市场化政策面临诸多问题，如政策制定者无法完全了解网络全局及集群主体特征的信息、市场公平性等。此外可在权衡所有集群主体的合作收益和成本的基础上，运用市场化的创新合作协议等方式，通过协议双方或多方间的收益转移弥补个别集群主体的私人损失，进而激励合作并实现集群整体创新合作绩效的提升。

本研究建立的合作网络是无权网络，仅考虑集群主体合作关系的有无，没有考虑集群主体间的竞争关系对创新合作决策的影响，后续研究可将无权合作网络扩展为考虑每对合作关系紧密程度的加权合作网络，同时在创新合作决策中引入竞争因素;对结论的实证性检验也是进一步的研究方向。

［1］李文博，张永胜，李纪明.集群背景下的知识网络演化研究现状评介与未来展望［J］.外国经济与管理，2010，32(10):10-19.Li Wenbo，Zhang Yongsheng，Li Jiming.Research present status and development tendency of knowledge network evolutions in the industrial clusters［J］.Foreign Economics ＆ Management，2010，32(10):10-19.(in Chinese)

［2］刘华容，曹休宁.产业集群中集群企业的合作创新问题研究［J］.科技进步与对策，2009，26(23):97-100.Liu Huarong，Cao Xiuning.Study on innovation cooperation in the industry cluster［J］.Science ＆ Technology Progress and Policy，2009，26(23):97-100.(in Chinese)

［3］黄玮强，庄新田，姚爽.基于创新合作网络的产业集群知识扩散研究［J］.管理科学，2012，25(2):13-23.Huang Weiqiang，Zhuang Xintian，Yao Shuang.Study on knowledge diffusion of industry clusters based on the innovation cooperation network［J］.Journal of Management Science，2012，25(2):13-23.(in Chinese)

［4］Jackson M O，Wolinsky A.A strategic model of social and economic networks［J］.Journal of Economic Theory，1996，71(1):44-74.

［5］Jackson M O，Watts A.The evolution of social and economic networks［J］.Journal of Economic Theory，2002，106(2):265-295.

［6］Goyal S，Joshi S.Networks of collaboration in oligopoly［J］.Games and Economic Behavior，2003，43(1):57-85.

［7］Zikos V.R＆D collaboration networks in mixed oligopoly［J］.Southern Economic Journal，2010，77(1):189-212.

［8］刘建平，申作平，莫超.复杂网络思想在上海世博会旅游产业集群中的应用［J］.经济地理，2009，29(12):2023-2027.Liu Jianping，Shen Zuoping，Mo Chao.The application of complex networks theory in tourism industry cluster of Shanghai World Expo［J］.Economic Geography，2009，29(12):2023-2027.(in Chinese)

［9］龚玉环，卜琳华，孟庆伟.复杂网络结构视角下中关村产业集群创新能力分析［J］.科学学与科学技术管理，2009，30(5):56-60.Gong Yuhuan，Bu Linhua，Meng Qingwei.An analysis of Zhongguancun industrial cluster's innovation ability based on complex network structure［J］.Science of Science and Management of S.＆ T.，2009，30(5):56-60.(in Chinese)

［10］杨锐，黄国安.网络位置和创新:杭州手机产业集群的社会网络分析［J］.工业技术经济，2005，24(7):114-118.Yang Rui，Huang Guoan.The network position and innovation:A social network analysis on Hangzhou mobile telephone industry cluster［J］.Journal of Industrial Technological Economics，2005，24(7):114-118.(in Chinese)

［11］Caspera S，Murray F.Careers and clusters:Analyzing the career network dynamic of biotechnology clusters［J］.Journal of Engineering and Technology Management，2005，22(1/2):51-74.

［12］Jackson M O.A survey of network formation models:Stability and efficiency［M］∥Demange G，Wooders M.Group Formation in Economics:Networks，Clubs，and Coalitions.Cambridge:Cambridge University Press，2005:11-57.

［13］Carayol N，Roux P.Behavioral foundations and equilibrium notions for social network formation processes［J］.Advances in Complex Systems，2004，7(1):77-92.

［14］Carayol N，Roux P.Knowledge flows and the geography of networks:A strategic model of small world formation［J］.Journal of Economic Behavior＆ Organization，2009，71(2):414-427.

［15］Jackson M O，Rogers B W.The economics of small worlds［J］.Journal of the European Economic Association，2005，3(2/3):617-627.

［16］田钢，张永安.集群创新网络演化的动力模型及其仿真研究［J］.科研管理，2010，31(1):104-115，125.Tian Gang，Zhang Yongan.Dynamical model and simulation for the evolution of industrial cluster innovation network［J］.Science Research Management，2010，31(1):104-115，125.(in Chinese)

［17］黄玮强，庄新田，姚爽.企业创新网络的自组织演化模型［J］.科学学研究，2009，27(5):793-800.Huang Weiqiang，Zhuang Xintian，Yao Shuang.Selforganizing evolvement model of innovation network［J］.Studies in Science of Science，2009，27(5):793-800.(in Chinese)

［18］Carayol N，Roux P，Yildizoglu M.Inefficiencies in a model of spatial networks formation with positive externalities［J］.Journal of Economic Behavior＆ Organization，2008，67(2):495-511.

［19］Carayol N，Roux P，Yildizoglu M.In search of efficient network structures:The needle in the haystack［J］.Review of Economic Design，2008，11(4):339-359.

［20］Jaffe A B.Real effects of academic research［J］.The American Economic Review，1989，79(5):957-970.

［21］Romer P M.Endogenous technological change［J］.Journal of Political Economy，1990，98(5):S71-S102.

［22］Carayol N，Roux P.Self-organizing innovation networks:When do small worlds emerge?［J］.European Journal of Economic and Social Systems，2005，18(2):307-332.

［23］韩瑞锋.遗传算法原理与应用实例［M］.北京:兵器工业出版社，2010:20-30.Han Ruifeng.The theory of genetic algorithm and its applications［M］.Beijing:Weapons Industry Press，2010:20-30.(in Chinese)

［24］Schaffer J D，Caruana R A，Eshelman L J，Das R.A study of control parameters affecting online performance of genetic algorithms for function optimization［C］∥Proceedings of the Third International Conference on Genetic Algorithms.San Francisco:Morgan Kaufmann Publishers Incorporation，1989:51-60.

［25］Davis G F，Yoo M，Baker W E.The small world of the American corporate elite，1982-2001［J］.Strategic Organization，2003，1(3):301-326.