利用周期性计算三维Gödel黑洞视界面积和熵的量子修正谱

刘显明,胡馨匀

(湖北民族学院 理学院， 湖北 恩施 445000)

利用周期性计算三维Gödel黑洞视界面积和熵的量子修正谱

刘显明,胡馨匀

(湖北民族学院 理学院， 湖北 恩施 445000)

利用一种新的半经典的周期性的方法计算了三维Gödel黑洞视界面积和熵的量子修正谱. 结果发现量子修正后的视界面积谱存在高阶的面积倒数的修正项，然而修正后的熵谱仍然是一个普适的常数，ΔSBH=2π. 结论表明熵谱不仅不依赖于黑洞的基本参量，而且不依赖于高阶的量子修正，因而在量子引力理论中熵谱比视界面积谱更有意义.

量子修正;黑洞;周期性

本文将进一步利用周期性的方法去研究三维Gödel黑洞视界面积和熵的量子修正谱.文献[10-11]已经分别利用拟正则频率和周期性计算了三维Gödel黑洞的视界面积和熵量子化谱. 他们的结论都表明三维Gödel黑洞视界面积和熵谱满足贝肯斯坦的最初假设.本文将利用出射波的周期性去计算在考虑量子修正后三维Gödel黑洞的视界面积和熵的量子谱，进一步探讨黑洞的量子化特征.

1 三维Gödel黑洞

式中G3是三维引力的引力常数，α是耦合常数.三维Gödel黑洞线元和规范势分别为：

(1)

和

度规函数：

积分常数υ,J,Q分别与三维Gödel黑洞的质量、角动量和电荷相关.由于存在非平凡的规范场，因此三维Gödel黑洞时空渐近的几何不仅不是AdS/dS时空，也不是卷曲的AdS时空.

其解为：

三维Gödel黑洞的事件视界的面积，霍金温度，角速度分别为：

(2)

对应的贝肯斯坦霍金熵为：

可以验证在此黑洞的事件视界上满足如下力学定律：

(3)

显然，定义υ,J分别为此黑洞的质量和角动量，方程(3)可以视为三维Gödel黑洞的热力学第一定律.

为了避免拖曳效应，可以引入所谓的“拖曳”坐标变换：dφ=dt/2αr

于是度规线元(1)将简化为2维的形式：

(4)

2 量子修正的事件视界面积谱和熵谱

本节将在考虑量子修正的前提下，利用出射波函数的周期计算三维Gödel黑洞的事件视界的面积谱和熵谱.

2.1 出射波函数和周期

为了得到黑洞振荡的周期，首先来计算在三维Gödel黑洞中出射粒子的波函数.为了简化起见，下面仅考虑无质量的标量场的例子.在弯曲时空之中，无质量标量场满足如下的克莱因-高登方程：

(5)

在方程(4)所描述的2维时空中，波函数Φ通常可用作用量S表示为：

(6)

于是把式(6)和式(4)带入式(3)，可以得到出射粒子的波函数方程为：

(7)

为了精确的求解方程(7)，可以把S(r,t)作如下展开：

(8)

其中i=1,2,3…，S0(r,t)是经典的作用量.

把式(8)式带入式(7)，并且按照ћ的各级进行展开，并整理后可得各级作用量Si(r,t)满足下面同一形式的微分方程:

(9)

根据在拖曳坐标系中的对称性，经典的作用量可以写为:

S0(r,t)=-(E-mΩ+)t+W(r)

(10)

其中，E是粒子的能量，m是粒子的角动量.

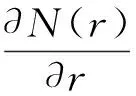
(11)

从式(11)可见出射波是周期函数，具有周期:

(12)

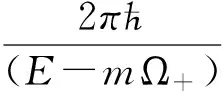
2.2 视界面积和熵的面积谱

正如文献[8-9,11]所指出，一个粒子的周期正是周期引力系统的周期，并且可以与系统的霍金温度建立起如下联系：

T=ћ/TBH

(13)

进一步利用关系E=ћω，周期(12)可以简化为:

(14)

另一方面利用式(2)可以得到辐射一个粒子带来的三维Gödel黑洞的视界面积的变化量为:

(15)

联立方程(13)，(14)和式(15)可得视界面积变化量为:

(16)

式(16)含了高阶修正的因子，利用式(7)可以进一步展开为:

显然可见，在量子修正的情况下，视界面积谱不是普适的常量，还有面积倒数的高阶修正项.

接下来，假定考虑量子修正的情况下，依然存在如下有效的热力学第一定律:

(17)

式中Teff是修正后有效温度:

(18)

于是利用方程(14),(17)和(18)，可以得到熵的量子化谱:ΔSbh=2π

由此可见即使在量子修正情况下，三维Gödel黑洞的熵谱依然为一普适的常量.修正后的结果与前面文献[12]中没有修正的结果是一样的.这说明熵谱不仅不依赖于黑洞基本参量，而且也不依赖于高阶的量子修正. 这说明在量子引力理论中熵谱比视界面积谱更为重要.

3 结论

本文利用周期性计算了在量子修正情况下的三维Gödel黑洞的视界面积谱和熵谱.结论表明视界面积谱存在高阶修正项，而熵谱始终保持为一普适常数.本文的结论进一步证实了贝肯斯坦的原始结论，同时得出了量子引力理论中黑洞的熵谱是比视界面积谱更有意义的论断. 这一结论期待着在后面的工作中得到更深入的理解.

[1] Hawking S W.Black hole explosions [J].Nature,1974,248:30-31.

[2] Hawking S W.Particle creation by black hole [J]. Comm Math Phys,1975,43(3):199-220.

[3] Bekenstein J D. The quantum mass spectrum of the Kerr black hole[J]. Lett Nuovo Cimento,1974,11:467-470.

[4] Hod S. Bohr's Correspondence Principle and The Area Spectrum of Quantum Black Holes[J]. Phys Rev Lett,1998,81:4293-4296.

[5] Maggiore M. Physical Interpretation of the Spectrum of Black Hole Quasinormal Modes[J]. Phys Rev Lett, 2008,100:141301.

[6] Vagenas E C. Area spectrum of rotating black holes via the new interpretation of quasinormal modes[J].JHEP,2008,0801:073.

[7] Medved A J M. On the Kerr quantum area spectrum [J]. Class Quant Grav, 2008, 25(20):205014.

[8] Zeng Xiao-Xiong, Liu Xian-Ming, Liu Wen-Biao. Periodicity and area spectrum of black holes[J].Eur Phys J C, 2012,72:1967.

[9] Liu Xian-Ming,Zeng Xiao-Xiong, Zhou Shi-Wei.Area spectra of BTZ black holes via periodicity[J].Science China Physics,Mechanics and Astronomy,2013,56(9):1627-1631.

[10] Li Ran. Quasinormal modes and entropy spectrum of three dimensional Godel black hole[J].Int J Mod Phys D, 2012, 21: 1250014.

[11] Li Hui-Ling.Area spectrum of the three-dimensional Gödel black hole[J].Chin Phys B,2012,21(12):120401.

[12] Banados M.Three-dimensional origin of Gödel spacetimes and black holes[J].Phys Rev D,2006,73:044006.

QuantumCorrectionstoAreaEntropySpectrumofThreeDimensionalGödelBlackHoleViaPeriodicity

LIU Xian-ming,HU Xin-yun

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

Quantum corrections to the area spectrum an the entropy spectrum of three dimensional Gödel black hole are calculated by a new simple semi-classical scheme via periodicity. In the presence of higher-order quantum corrections, the area spectrum is found to be corrected by inverse area terms while the entropy spectrum is found to have a universal form, ΔSBH=2π. The results show that the entropy spectrum is independent of not only the Gödel black hole parameters but also the higher-order quantum corrections, which implies that the entropy spectrum is more natural than the area spectrum in quantum gravity theory.

quantum corrections;black hole;periodicity

2013-08-22.

国家自然科学基金项目(11365008);湖北省教育厅项目(Q20131901).

刘显明(1980- )，男(侗族)，博士，讲师，主要从事理论物理的研究.

P145.8

A

1008-8423(2013)03-0241-04