基于FPGA的双T选频网络的设计与实现

李 哲，高 波，马家君

（1.西安邮电大学 电子工程学院，陕西 西安 710061；2.西安电子科技大学 技术物理学院，陕西 西安 710071）

激光陀螺是一种基于Sagnac效应的光学陀螺[1-2]，在棱镜式激光陀螺中，控制光程长的过程中调制了300 Hz相敏信号，在解调的过程中需要将这单一频率解调并进行分析处理，得到误差信号，所以对解调算法要求很高。解调电路的主要噪声来自于激光陀螺小抖动偏频的高频抖动信号、去动态锁区所加的人工噪声信号、陀螺输出脉冲的低频信号以及系统噪声。使用现场可编程门阵列(FPGA)设计数字滤波器时，现多采用 FIR、IIR带通滤波器解调信号。传统的FIR和IIR滤波器需要较高的滤波阶数和资源，同时伴随着较大的运算量。高阶FIR、IIR参数的确定方法基本通过计算机软件来实现，且难以循环修改大量滤波系数[3-4]，具有一定局限性。这样信号解调就需要降低滤波器阶数和提高选频效果。

双T网络处理单一频率或频带很窄的信号有很好的滤波特性，且结构简单，在实际应用时多用于针对单一频率的陷波器或者选频器中[5-6]。但目前均是在模拟电路中被广泛应用。本文针对其滤波特性，将无源双T网络连接到运放的负反馈端作为选频网络，根据系统需要进行参数计算，有效地将其运用到提取相敏信号的数字滤波电路中。

1 双T选频网络的性能分析

如图1所示，双T选频网络可以看作是将双T带阻滤波器（如图1虚线部分）和一个反馈电阻并联到运放的负反馈端。其中无源带阻滤波器可以看成是1个T型低通滤波器和1个T型高通滤波器并联而成的带阻滤波器，当改变这个带阻滤波器的品质因数时，它就变成了单一频率的陷波器，其频率特性直接决定了双T选频网络的选频特性。为了使选频特性更理想，参考文献[7]介绍了一种不对称双T选频网络电容电阻的选择，取R2=R，R1=9R，R3=3/4R，C2=C，C1=1/3C，C3=10/9C，品质因数Q0=0.356。其传递函数为：

图1 选频放大器原理图

其中ω0为对称双T带阻滤波器的中心频率：

在此基础上，连接运放负反馈构成双T选频网络的闭环回路，其闭环增益为：

其中：

当不存在双T带阻滤波器时，系统是一个基本放大器，AVf为这个放大器的增益。

将式(4)和式(1)带入式(3)得：

其中：

Q为选频网络的品质因数。Q值越大，选频效果越好[8]，相对带宽也越小。系统延时也随着Q值增大而上升。其频率特性如下：

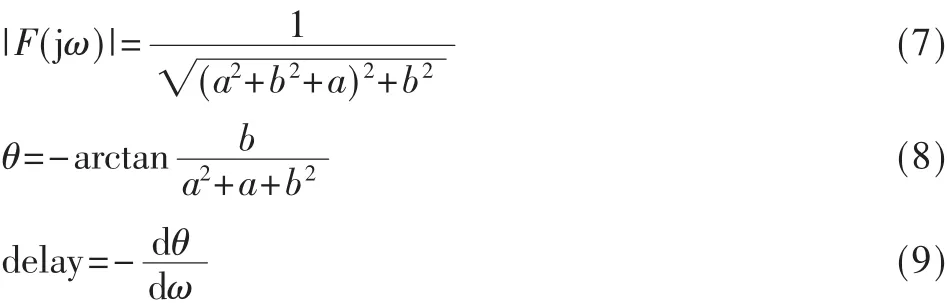
其中：

图2显示了选频网络的频率特性，尖峰部分带宽取决于Q值。

图2 滤波器频率特性

选频网络的带宽随着Q值的增大而减小。下面介绍电路设计，并通过仿真分析窄带宽双T选频网络在棱镜式激光陀螺光程回路中信号解调的优点。

2 棱镜式激光陀螺光程控制回路

棱镜式激光陀螺光程控制回路通过改变谐振腔内部气体折射率来改变光在气体介质内的光程，达到稳定的 目 的[1，9]。

控制环节输出300 Hz纵模频率调制信号到压电陶瓷片上，使压电陶瓷片膨胀和收缩，从而改变谐振腔气体介质密度，使其折射率发生相应变化，激光程长在小幅度范围内周期性变化。激光程长的变化将使得光电传感器输出的拍频信号上叠加一个300 Hz光强调制信号，通过识别该信号的频率和相位判断当前激光工作频率在增益曲线上的位置。当激光工作频率位于中心频率v0右侧时，减小输出到加热器的控制电压，使激光器内气体冷却，压强减小，折射率变大，从而光程增大，激光的工作频率则向着v0的方向减小；当激光工作频率位于中心频率v0左侧时，增大输出到加热器的控制电压，使激光器内气体加热，压强增大，折射率变小，从而光程减小，激光的工作频率则向着v0的方向增大，从而完成谐振腔频率的控制。

由于回路中存在着加热器这一主要延时环节，所以在滤波器环节中延时要求不高，可以通过增大Q值的方法来减小通带带宽，从而实现单一频率的滤波。

3 FPGA电路设计及仿真

3.1 传递函数S域、Z域的变换

在数字滤波器设计时不能只拘泥于具体电容电阻而要考虑每个元件参数的变化对滤波器灵敏度的影响，从而得到精确的滤波器参数，且能设计出极窄通带带宽的滤波器。根据系统需要，本文设计的滤波器取BW=2 Hz，代入式(12)得 Q=150。

使用脉冲响应不变法对双T选频网络进行数字化，得到其在4 kHz采样频率下的传递函数。代入Q=150，Q0=0.356，中心频率 ω0=300 Hz，可得：

式(13)的极点分别为0.889 6+0.453 3i、0.889 6-0.453 3i，均在单位圆内。因此，系统是稳定的。

在Matlab中对得到的选频网络的传递函数和传统FIR、IIR滤波器在相同输入的情况下进行建模仿真，如图3所示。

图3 信号滤波建模

输入信号分别采用 300 Hz、400 Hz及270 Hz的信号与白噪声进行叠加，取FIR、IIR滤波参数通带带宽2 Hz，阻带衰减为80 dB。

在上述条件下，通过双T选频网络、FIR、IIR三种滤波的信号峰峰值分别为10 000、0.02和0.2。

图4自上而下分别为原始信号、双T选频网络、FIR、IIR输出波形。

图4 原始信号及滤波效果

三种滤波器阶数分别为 2、298、40，相比之下，FIR、IIR阶数远比双T选频网络要高，且滤波后的信号幅值较低，这样就导致噪声对解调后的信号影响大，信噪比低，使得信号的可调节范围远比双T选频网络小得多。

3.2 FPGA电路设计及仿真

通过得到的传递函数式（13），采用直接-II型滤波器结构得到如图5所示的电路运算结构。

图5 直接II型滤波器结构

差分方程为：

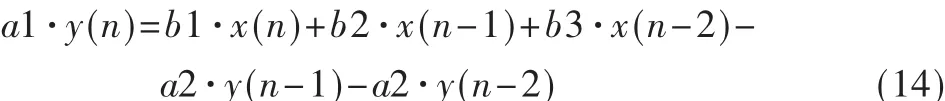
根据式(14)完成双T选频网络的FPGA功能，采用Verilog硬件描述语言和自顶向下的数字系统设计方法进行电路设计和功能仿真。

由于滤波器的系数均是以小数的形式表示出来，使用定点运算时需要将其转换为二进制数，系数在一定意义上放大了2的整数次方倍，在乘法运算时会出现输出信号溢出现象，这就需要一个高位宽的寄存器，同时在输出信号时需要进行数据的去头和截尾，不能保证滤波输出的精度，且使用定点运算时要对运算的最大值进行估算，有一定的局限性。本设计将定点数转换为单精度浮点数，然后再进行乘加运算，最终将浮点运算的结果转换成定点数作为滤波输出。这样就在有限的数据位宽中进行有效的运算处理，不会出现溢出现象。

将棱镜式数字激光陀螺实际工作时采集的数据作为激励，仿真结果得到一段幅值稳定、无振荡效果的输出波形。

实际系统中，解调出的波形会由于电路中的干扰和滤波的效率而存在一定的噪声，当图6仿真波形存在噪声较大时，即当前激光工作频率在增益曲线上的位置会随着噪声的随机变化产生波动，导致误差信号解调出现微小扰动。故解调信号的信噪比也决定了系统控制的精确程度。

图6 ModelSim仿真结果

下面通过实验的方法对比双T选频网络和传统的IIR滤波器在实际系统中使用时的信噪比情况。

4 实验分析

在分析棱镜式激光陀螺稳光程回路时，主要是通过在系统的输入端加一级阶跃并观察其瞬态响应来调节回路参数。现用本文设计的滤波器替换原有的IIR滤波器，并使用上位机软件对解调信号进行采集，实验结果如图7所示。

图7 实际调试瞬态响应

对稳定后的信号求平均值和标准差，采用本文设计的窄通带带宽双T选频网络比使用FIR滤波器信噪比提升了200%。

实验表明，采用双T选频网络后对系统对噪声抑制有很明显的作用，对信号信噪比有大幅度提升。在调试过程中能够更清晰地反应出系统的阶跃瞬态，能够通过改变参数更精确地调节回路的响应速度和控制精度。

在单一频率滤波时，双T选频网络噪声抑制效果明显。在棱镜式激光陀螺光程控制回路中，应用双T选频网络解调出的相敏信号进行误差运算。对比改进前后，计算误差信号的精确程度提高了一个数量级。

在使用FPGA设计双T选频数字滤波器时，不需要利用Matlab工具箱生成大量高阶滤波器参数，可以直接通过所需幅频特性、相频特性对滤波器进行设计，通过数字化的方法进行FPGA电路设计，大大节省了运算量和资源。应用在实际工程中，有着良好的推广前景。

[1]刘健宁，蒋军彪，石顺祥，等.全反射棱镜式环形激光器合光输出及陀螺精度特性分析[J].中国激光，2013，40(1)：0102002.

[2]张文，金世龙.环形激光陀螺光路控制系统的研究[C].2004全国光学与光电子学学术研讨会，2005全国光学与光电子学学术研讨会，广西光学学会成立20周年年会论文集，2005.

[3]郝逸轩.数字滤波器的优化设计研究[D].长沙：长沙理工大学，2012.

[4]唐博，李锦明，李士照.基于FPGA的高阶FIR滤波器强抗干扰数据采集系统[J].电子技术应用，2012，38(9)：89-92.

[5]王翠珍，唐金元.对称RC双T网络在选频放大电路中的应用[J].科技信息，2010(031)：I0078-I0079.

[6]蒋亚超，杨勇，李兴东，等.三种双T网络陷波电路分析与比较[J].电子技术(上海)，2011，38(001)：70-72.

[7]李林和.采用不对称RC双T反馈电路的选频放大器分析与设计[J].天津轻工业学院学报，2003，18(2)：34-38.

[8]苏立国，付松年，朱燕杰，等.应用新型双 T选频网络的OFCS光检测放大器[J].电子技术应用，2001，27(5)：55-57.

[9]李哲.全数字化激光陀螺控制系统设计[J].激光与光电子学进展，2010(5)：87-91.