基于遗传算法的差值形态滤波尺度参数优化方法研究
吕 博 张永祥 柯 维
海军工程大学,武汉,430033
0 引言
数学形态学是基于积分几何和随机集论建立起来的数学方法[1],该方法的信号处理只取决于待处理信号的局部特征,利用预先定义的结构元素来局部修正信号的几何结构,以达到提取信号、抑制噪声的目的,因此结构元素的选择对处理结果具有非常大的影响。差值形态滤波器作为形态滤波器的一种,具有良好的提取冲击信号的能力,因此常常用于轴承的故障诊断[2-3]。目前轴承的故障诊断方法主要有包络解调与谱峭度法,但是包络解调方法需要选择窄带滤波参数,将高频振荡信号从噪声中分离出来,且窄带滤波参数的选择对处理效果有很大影响[4],因此对使用者的专业知识和操作经验提出了一定的要求。谱峭度法能根据峭度最大化原则自动选择带通滤波器参数,取得一定的诊断效果,但诊断效果受噪声的影响较大,在强噪声背景下往往难以取得理想的效果。而差值形态滤波器不仅不依赖所处理信号的先验知识,且能够很好地克服噪声的干扰。但在运用过程中同样存在结构元素尺度难以确定的问题,文献[5]设计了多尺度混合形态滤波器,得到了周期性故障冲击特征,在结构元素的选取上采取的是多次尝试的方法。文献[6]中使用结构元素尺度为0.6倍的齿轮冲击周期的扁平形结构元素进行形态解调,取得了较好的效果。
本文在介绍数学形态基本运算的基础上,主要研究了基于遗传算法下的结构元素尺度的选择及优化方法。仿真和试验研究结果证明,经该方法得到的优化尺度下的处理效果优于非优化尺度下的处理效果和传统包络解调法。
1 差值形态滤波的基本原理及尺度优化
1.1 数学形态滤波的基本运算
形态学的基本运算为膨胀运算、腐蚀运算、开运算和闭运算[7],以及开闭运算和闭开运算。假定采样得到的待处理的一维信号为f(n),其定义域F= {0,1,…,N-1},结构元素为g(m),定义域G= {0,1,…,M-1},且N >M,则f(n)关于结构元素g(m)的腐蚀运算和膨胀运算定义为
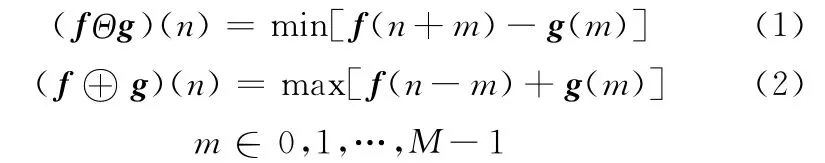
式中,Θ和⊕分别代表腐蚀运算和膨胀运算。
f(n)关于g(m)的开运算和闭运算分别定义为
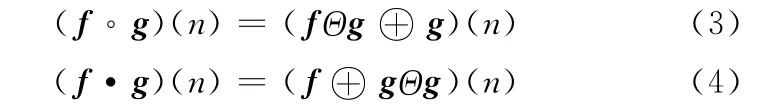
通过级联开运算、闭运算可组成具有不同作用的形态滤波器。常见的级联有两种,第一种级联组合为开-闭和闭-开组合形态滤波器:
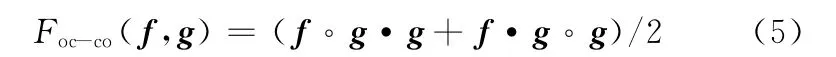
这种滤波器主要有滤除基线漂移[8]和滤除噪声[9]两种用途,第二种级联组合为差值形态滤波器[10]。下面主要介绍差值形态滤波器的应用。
1.2 差值形态滤波器
差值(DIF)形态滤波器定义为

上式定义的差值形态滤波器可以同时提取正负冲击脉冲,这是因为
而f·g-f和f-f·g正好是形态学Top-Hat变换[11]的两种形式。f·g-f被称为黑 Top-Hat变换,可以用来提取负冲击脉冲;f-f·g被称为白Top-Hat变换,可以用来提取信号中的正冲击脉冲,因此式(6)定义的差值形态滤波器,可以同时提取正负脉冲冲击信号。
1.3 结构元素的选取
对已知信号进行形态滤波时,滤波效果取决于形态滤波器的级联组合方式和结构元素两个方面。结构元素的要素包括形状、高度和长度。选取结构元素的形状时要尽量接近待处理信号的图形特点,因为只有与结构元素形状相匹配的结构基元才能被保留,常见的结构元素形状有扁平形、直线形、三角形、椭圆形、半圆形、正弦形及抛物线形等。其中常用的有扁平形g(n)= [00000]、三角形g(n)= [0 1 2 3 2 1 0]和正弦形g(n)=[0 0.5878 0.9511 0.9511 0.5878 0],本 文 使 用的结构元素为扁平形结构元素。结构元素的高度一般根据经验选取,对于三角形的结构元素,高度取信号主要轮廓高度的2%~5%时,效果较好[10]。结构元素尺度的选取大多靠经验选取,文献[6]中使用结构元素尺度为0.6倍的齿轮冲击周期的扁平形结构元素进行形态解调时,提取出了轴承的故障冲击信号。
2 基于遗传算法的结构元素尺度的优化方法
结构元素尺度的选取对滤波效果具有决定性作用,当无法确定采用何种结构元素时,采用扁平形结构元素往往能取得不错的效果,本文采用扁平形的结构元素。差值形态滤波的关键是确定结构元素的尺度,目前对于结构元素尺度的选取问题尚没有定论,主要是根据经验和尝试等方法选取,因此很多情况下难以取得满意的效果,同时也限制了差值形态滤波的使用。遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化算法,其本质是一种高效、并行、全局搜索的方法。本文提出一种基于遗传算法的结构元素尺度设计方法。设计步骤如下:
(1)结构元素尺度参数的编码。这里采用二进制编码方法对结构元素的尺度参数进行编码,其大小代表了结构元素的尺度,这里取最小尺度为2,最大尺度略大于Fs/f1,其中,Fs为采样频率,f1为故障冲击信号的一倍频。
(2)初始种群的生成。随机产生N个个体作为初始群体,并设置最大代数T。基因群体的取值要综合考虑,太小时,容易收敛到局部最优解;太大时,每次循环的计算量较大,收敛速度也会变慢,一般取为20~100。
(3)适应度函数的确定。适应度函数是用于区分不同个体代表的尺度下差值形态滤波效果好坏的目标函数。为了表征滤波的效果,本文采用故障频率信号对噪声的比值来表征滤波效果。定义η=(E1+E2+E3)/E,其中E1、E2、E3分别为滤波后信号频域内故障频率的一倍频至三倍频的能量的平方,E为滤波后信号频域内零到信号五倍频的总能量。
(4)个体适应度的计算。对个体计算前,首先要进行解码处理,之后将个体所表示的尺度对信号进行滤波处理,并计算对应的适应度。
(5)遗传算子和运行参数的确定。遗传算法使用选择算子对群体中的个体进行优胜劣汰操作,其基本操作为选择、交叉和变异。选择是根据各个个体的适应度值,从当前群体中选出优良的个体遗传到下一代群体中;交叉运算是产生新个体的主要方法,本文中通过交叉操作可得到新的结构元素尺度,交叉概率Pc一般在0.4~0.99之间取值;变异运算只是产生新个体的辅助方法,能够改善遗传算法的局部搜索能力,维持群体的多样性,防止出现早熟现象。变异概率Pm一般取值范围是0.0001~0.1。
(6)终止条件判断:若适应度函数小于设定值,则转到步骤(2)继续计算;若适应度函数等于或大于设定值,则以进化过程中所得到的具有最大自适应度的个体作为最优解输出,终止运算。
3 数值仿真
为了验证差值形态滤波器在提取冲击脉冲方面的作用,取以下信号进行仿真分析:

其中,x= (1+0.3sin(20πt))cos(300πt)+ (1+0.4sin(10πt))cos(700πt),为 调 制 信 号,η(t)=square(140πt,3)为一方波信号,n(t)=rand(1,8000t)为噪声信号,采样频率Fs=8000Hz,其中y(t)的时域和频域图如图1和图2所示;η(t)为频率为70Hz的方波脉冲冲击信号,图3为其局部图;n(t)为白噪声信号。

图1 调制信号y(t)时域图

图2 调制信号y(t)的频域图

图3 方波脉冲冲击信号
使用本文提出的算法对尺度进行优化,得到最优尺度为n=25,使用g=zeros(1,25)的扁平形结构元素的差值形态滤波后的效果如图4所示。分别使用尺度为68(约为0.6倍的齿轮冲击周期长度)和包络解调(带宽为1300~1800Hz)对信号y(t)进行故障信号提取,并对提取后的信号进行FFT变换,得到的结果如图5、图6所示。
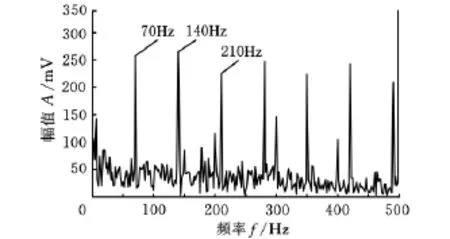
图4 尺度为25时滤波后的频域图
通过对比,我们不难发现,在优化尺度下差值形态滤波的处理要优于包络解调的处理效果,而尺度未经优化的差值形态滤波效果比包络解调的处理效果略差。计算结构元素尺度为25和68的频域内比值η分别为43.1742和19.8622,说明对差值形态滤波器而言,尺度优化是必要的。

图5 尺度为68时滤波后的频域图

图6 包络解调后的处理效果图
4 试验研究
为验证上述差值形态滤波尺度设计方法及其在滚动轴承故障诊断应用中的有效性,进行了试验研究。试验装置由滚动轴承、调速电机、加载机油泵等组成。将6204型号的轴承内圈用线切割机切了一道宽0.1mm、深0.2mm平行轴承轴线方向的沟槽。测试时,滚动轴承的运行转速从200r/min 到 3000r/min,信 号 的 采 样 频 率 为100kHz,采样长度为10 000点。其典型振动信号如图7所示,图8为其频谱图。图中滚动轴承的转速为2967r/min,此时滚动轴承内圈的故障频率为268Hz。
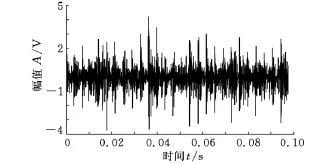
图7 滚动轴承源信号时域图

图8 滚动轴承源信号的频域图
根据前面分析,利用前述遗传算法进行结构元素尺度优化设计,基因种群为20,遗传概率为54%,杂交概率为45%,变异概率为1%。根据工程经验,其比值η达到40时,就可以很好地提取故障冲击信号。经3代优化后得到优化的尺度为73,图9为优化尺度参数下滤波后的频域图;图10为结构元素尺度为229时,即在齿轮冲击周期长度(100 000/268≈382)的0.6倍下的滤波后的频域图;图11为传统共振解调后的频域图。

图9 尺度为73时滤波后的频域图
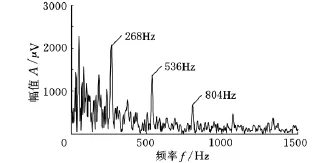
图10 尺度为229时滤波后的频域图

图11 共振解调后的频域图
从图8滚动轴承源信号的频域图中可以看出,滚动轴承故障冲击信号已经完全湮灭在噪声中而难以分辨。而滚动轴承源信号经差值形态滤波后,在图9、图11中,已排除了大部分噪声的干扰,从而很容易得到滚动轴承的故障频率及其倍频,从而可以较准确地确定故障部位,但采用齿轮冲击周期长度的0.6倍的尺度进行滤波后,其噪声相对图9较大,通过计算,上述两种尺度下的比值为:ηc=40.721,ηd=12.826,说明采用本文中优化方法得到的尺度对滚动轴承进行故障诊断可以取得更好的效果。
图11为采用传统共振解调方法对源信号进行解调后的频域图,从图中看出效果要劣于优化尺度下的差值形态滤波的效果,在故障频率及其倍频周围有很大的瓣频出现,给我们对滚动轴承的故障诊断带来了很大的干扰,但效果优于非优化尺度下的差值形态滤波效果。
5 结论
(1)差值形态滤波提取故障冲击信号的效果与结构元素密切相关,为了达到在不同条件下得到最好滤波效果的目的,必须对结构元素进行实时优化。
(2)经过仿真和试验表明,本文提出的基于遗传算法的结构元素尺度优化设计方法是可行的,可以应用于各种工况下滚动轴承的故障诊断。
(3)差值形态滤波可有效的提取滚动轴承故障特征,在优化后取得的效果要优于传统共振解调方法的效果。
[1]Heyden T,Woemle C.Dyanm Ices and Flatnessbassed Control of a Kinem Atically Undetermined Cable Suspension Manipulator[J].Multibody System Dynam Ices,2006,16(3):175-177.
[2]李豫川,伍星,柳小琴,等.基于形态滤波和独立分量分析的轴承故障盲分离[J].电子测量技术,2010,33(9):101-104.Li Yuchuan,Wu Xing,Liu Xiao,et al.Blind Separation for Bearing Faults Based on Morphological Filters and Ica[J].Electronic Measurement Technology,2010,33(9):101-104.
[3]王学志,王立东.广义数学形态滤波器在异步电动机轴承故障诊断中的应用[J].矿山机械,2011,39(4):112-115.Wang Xuezhi,Wang Lidong.Application of Generalized Mathematical Morphology Filter to Fault Diagnosis of Bearing of Asynchronous Motors[J].Mining Machinery,2011,39(4):112-115.
[4]Rubini R,Meneghetti U.Application of The Envelope and Wavelet Transform Analyses for The Diagnosis of Incipient Faults in Ball Bearings[J].Mechanical System and Signal Processing,2001,15(2):287-302.
[5]郝如江,卢文秀,褚福磊.形态解调用于滚动轴承故障信号的特征提取[J].中国机械工程,2009,20(2):197-201.HaoRujiang,Lu Wenxiu,Chu Fulei.Morphological Filters in Feature Extraction for Rolling Bearing Defect Signals[J].China Mechanical Engineering,2009,20(2):197-201.
[6]郝如江,卢文秀,褚福磊.形态解调在滚动轴承故障声发射信号处理中的应用[J].清华大学学报(自然科学版),2008,48(5):812-815.HaoRujiang,Lu Wenxiu,Chu Fulei.Morphology Filters for Analyzing Roller Bearing Fault Using Acoustic Emission Signal Processing[J].J.Tsinghua Univ.(Sci.& Tech.),2008,48(5):812-815.
[7]Serra J.Morphological Filtering:An Overview[J].Signal Processing,1994,25(6):107-111.
[8]刘艳丽,赵为松,李海坤,等.基于形态滤波的脉搏信号基线漂移消除方法研究[J].合肥工业大学学报,2011,34(4):525-528.Liu Yangli,Zhao Weisong,Liu Haikun,et al.Reasearch on Removing Baseline Wandering of Pulse Wave Signal Based on Morphological Filter[J].Journal of Hefei University of Technology,2011,34(4):525-528.
[9]李春枝,何荣建,田光明.数学形态滤波在振动信号分析中的应用研究[J].计算机工程与科学,2008,30(9):126-128.Li Chunzhi,He Rongjian,Tian Guangming.Research on The Application of The Mathematical Morphology Filtering in Vibration Signal Analysis[J].Computer Engineering&Science,2008,30(9):126-128.
[10]沈路,周晓军,张文斌,等.基于形态滤波与灰色关联度的滚动轴承故障诊断[J].振动与冲击,2009,28(11):17-20.Shen Lu,Zhou Xiaojun,Zhang Wenbin,et al.Fault Diagnosis of Rolling Element Bearing Based on Morphological Filter and Grey Incidence[J].Journal of Vibraton and Shock,2009,28(11):17-20.
[11]崔屹.图像处理与分析-数学形态学方法及应用[M].北京:科学出版社,2000.

