时滞对振动主动控制系统控制效果的影响分析
张伟中 张 斌 伍晓红 孙 清
1.浙江机电职业技术学院,杭州,310053 2.河南省电力勘测设计院,郑州,450007 3.西安交通大学,西安,710049
0 引言
时滞系统普遍存在于自然和工程实际中,从自然界到人类社会,从自然科学、工程技术到社会科学,时滞现象无处不在[1-12]。在精密仪表、数控机床等自动化产品结构涉及的振动主动控制领域也不可避免地存在着时滞现象,传感器信号的采集和传输、控制器的计算、作动器的作动过程等,都会导致作用于结构的控制力产生时滞[13-14]。时滞的存在使受控系统成为无限维系统,增加了其动力特性的复杂性,而且时滞反馈系统具有超越特征方程和无限多特征值,给系统的稳定性分析增加了难度,因此数值方法成为了分析时滞控制系统稳定性的有力工具。精细积分方法是为解决结构动力学计算而提出的,该算法简单且计算精度很高,近年来在计算动力学问题、最优控制问题以及偏微分方程中得到应用[15-16]。但是对于时滞受控系统,当控制力与系统的位移和速度相关时,需要对荷载向量逐步进行赋值,故应用精细积分方法时须先对其进行修正。本文对精细积分方法进行改进,计算含时滞受控系统的动力学方程,得到了在不同时滞量下系统的响应。
1 含时滞振动控制系统的动力学方程
含双时滞受控系统的动力学方程如下:

2 时滞受控系统动力响应的精细积分方法
首先进行变量代换,引入一对对偶变量,令

则式(1)可以表示为
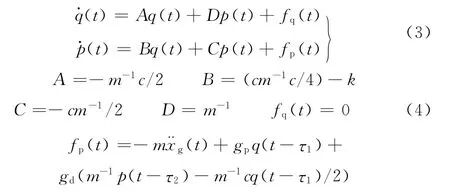
令

则式(5)为非齐次微分方程,先求解其齐次解,齐次方程形式如下:

设时间步长为τ,则

令v0=v(0),v1=v(τ),v2=v(2τ),…,vk=v(k τ),则

下面求T,有
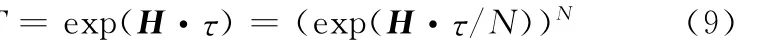
令Δt=τ/N,当取N=2n很大时,Δt很小,采用泰勒级数展开:

从而
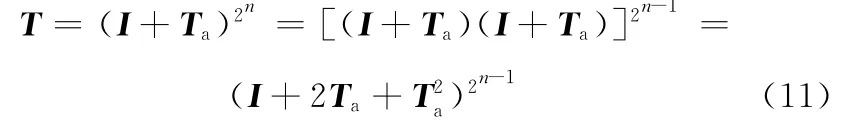
由于Ta的元素值相对于单位矩阵I非常小,为减小计算机的舍入误差,编程时单位矩阵I不参与累加及乘法运算,而是通过对Ta=2Ta+T2a进行n次循环计算得到Ta,当循环结束时,有

得到了齐次方程的解后,下面求解式(5),设非齐次项在时间步长(tk,tk+1)内为线性变化,则式(5)可写为
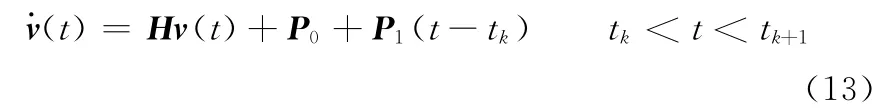
其中,P0= P(tk),P1= (P(tk+1)-P(tk))/τ。式(5)的解可表示为

将t=tk+1代入式(14),由于exp(H(tk+1-tk))=exp(Hτ)=T,因此有
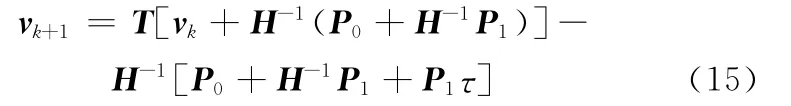
在文献[16]的算例中,每个时间点的荷载向量P0和P1都是已知的,在程序的初始可以提前赋值,但对本文求解的含有时滞的振动控制方程,由于控制力gpx(t-τ1)和gdx·(t-τ2)与该时间点τ1之前的位移以及τ2之前的速度有关,而系统的位移和速度是待求解的,无法提前预知,故荷载向量无法在程序初始时赋值,因此,P0和P1的求解成为解决问题的关键。
选取合适的时间步长τ,令τ与时滞量τ1和τ2满足下述关系:

式中,l、p均为正整数。
设l<p,对第k个时间步长的荷载向量进行计算,当k<l-1时,有

对 k = l-1, 设 vk= [q(tk)p(tk)]T=[qkpk]T,则有
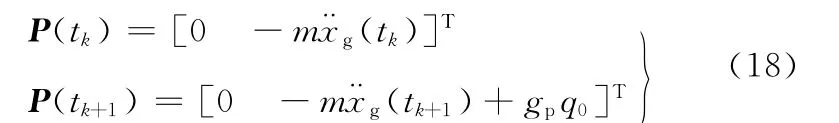
对l≤k<p-1,有
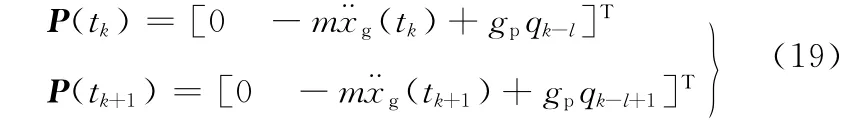
对k=p-1,有

对k≥p,有

其中,qk-l、pk-p、qk-p等在第k步计算时已经为已知,此时可以逐步对P0和P1赋值,再根据式(15)求出每一步的响应。对于l≥p的情况,过程类似,此处不再赘述。
3 算例结果及分析
选取Elcentro波,峰值加速度a为200cm/s2,波形如图1所示。取系统参数为:m=1kg,c=3 N·s/m,K =500N/m,初始条件为x(0)=0,(0)=0,则动力方程表达为


图1 Elcentro波
采用前述精细积分方法,取时间步长为0.01s,当系统没有控制时,时程响应曲线如图2所示。

图2 无控制时系统时程响应

图3 取gp=-0.020 000N/m,gd=-2.388 877N·s/m时系统时程响应

图4 取gp=-0.199 960N/m,gd=-11.470 657N·s/m时系统时程响应
从图3~图5可以看出,随着控制增益gp和gd取值的增大,系统的响应趋于减小,则控制效果越来越好。

图5 取gp=-1.996 016N/m,gd=-41.866 380N·s/m时系统时程响应
以上是不考虑时滞的情况,但是在工程实际中,时滞是不可避免的,下面采用精细积分算法分别计算不同时滞情况下的系统响应,并将每种时滞组合下系统响应的最大值即系统响应峰值与相应的时滞组合绘制分布图。
(1)当 gp= -0.02N/m,gd= -2.388 877 N·s/m时,系统响应峰值位移量S分布如图6所示。
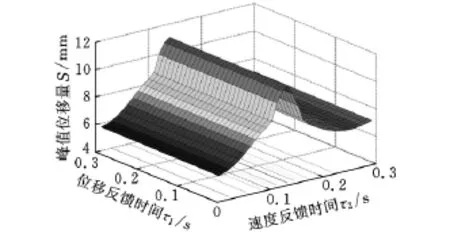
图6 系统响应峰值位移量S分布图
(2)当 gp= -0.199 960N/m,gd=-11.470 657N·s/m 时,时间响应分别为0~0.3s和0~0.06s时,系统响应峰值位移量S分布如图7所示。

图7 系统响应峰值位移量S分布图
(3)当 gp= -1.996 016N/m,gd=-41.866 380N·s/m时,系统响应峰值位移量S分布如图8所示。

图8 系统响应峰值位移量S分布图
从图6、图7a和图8a可以看出,系统的峰值分布主要随τ2发生变化,这是由于在三组最优控制中,gd都明显大于gp,因此与gd相关的时滞量τ2就对系统的响应起了决定性的作用。尽管系统响应峰值随τ2增大上升之后又有回落,但是此时已经失去了控制效果,在图6中回落的最低点峰值S=0.006 763 3m(τ1=0.19s,τ2=0.25s),与系统无控的响应峰值位移量S=0.007 329m相比,控制效果并不明显。为此文中对时滞影响的讨论主要集中在响应峰值随时滞变化的上升阶段。
因图7a和图8a中的峰值过大,为清楚描述峰值随时滞变化的上升过程,将时滞的变化范围缩小到0.06s和0.03s以内,分别得到图7b和图8b。
比较图6、图7b和图8b可以看出,对于固定的控制增益,在变化的初期随着时滞的增大,系统的响应峰值也增大。当时滞较小时,选择较大的控制增益可以获得较好的控制效果。
在图6中,当τ1=0.01s,τ2=0.01s时,系统响应的峰值位移量S=0.005 83m,而图7b中,当τ1=0.01s,τ2=0.01s时,系统的响应峰值S=0.003 388m,同无时滞情况下的两种增益取值下的峰值对比趋于一致。但是同时,随着时滞的增大,较大的控制增益会使系统更快地失去稳定,如图8a,当τ1=0.01s,τ2=0.04s时,系统响应的峰值已经达到了1 741 100m,发散速度很快,而在图6中,当τ1=0.01s,τ2=0.04s时,系统响应的峰值位移量S仅为0.006 227m,仍具有一定的控制效果。
4 结论
(1)最优控制方法对于无时滞系统可以获得很好的控制效果,但对考虑时滞情况的受控系统则有一定的局限性,如果减小控制增益的加权矩阵R,得到的最优控制增益将增大,理论的控制效果也更好。
(2)时滞对系统控制效果的影响程度与反馈增益有关,随着增益的增大而增大,并且时滞的增大会导致控制增益较大情况下系统响应很快发散;同时,较大的控制增益会使系统更快地失去稳定;为此应适当地调节时滞量和反馈控制增益,使它们相匹配,这样可以使系统保持稳定状态。因此应根据控制过程中的时滞量选择合理的控制增益,以获得更好的控制效果。
[1]Briat C,Sename O,Lafay J F.Memory-resilient Gain-scheduled State-feedback Control of Uncertain LTI/LPV Systems with Time-varying Delays[J].Systems & Control Letters,2010,59(8):451-459.
[2]Cacace F,Germani A,Manes C.An Observer for a Class of Nonlinear Systems with Time Varying Observation Delay[J].Systems & Control Letters,2010,59(5):305-312.
[3]胡俊峰,张宪民.一种新型两自由度柔性并联机械手的主动振动控制及其仿真[J].中国机械工程,2010,21(17):2017-2020.Hu Junfeng,Zhang Xianmin.Active Vibration Control and Its Simulation of a Novel 2-DoF Flexible Parallel Manipultator[J].China Mechanical Engineering,2010,21(17):2017-2020.
[4]Terje A,Castro I T.A Delay-time Model with Safety Constraint[J].Reliability Engineering &System Safety,2009,94(2):261-267.
[5]Shaltaf S.Neuro-fuzzy Based Time-delay Estimation Using DCT Coefficients[J].ISA Transactions,2007,46(1):21-30.
[6]Jones B,Jenkinson I,Wang J.Methodology of Using Delay-time Analysis for a Manufacturing Industry[J].Reliability Engineering & System Safety,2009,94(1):111-124.
[7]Nayfeh A H,Charming C.Perturbation Methods in Nonlinear Dynamics:Applications to Maching Dynamics[J].Journal of Manufacturing Science and Engineering,1997,119(4):485-493.
[8]孙仁斌,胡军浩.受扩散与时滞及食物限制影响的人口模型[J].数学的实践与认识,2006,36(5):135-139.Sun Renbin,Hu Junhao.Population Model Effected by Diffusion and Time Delay and Dood-limited[J].Mathematics in Practice and Theory,2006,36(5):135-139.
[9]胡海岩.振动主动控制中的时滞动力学问题[J].振动工程学报,1997,10(3):274-279.Hu Haiyan.On Dynamics in Vibration Control with Time Delay[J].Journal of Vibration Engineering,1997,10(3):274-279.
[10]Liu Zixin,LüShu,Zhong Shouming,et al.Stabilization Analysis for Discrete-time Systems with Time Delay[J].Applied Mathematics and Computation,2010,216(7):2024-2035.
[11]Liu Duyu,Zhong Shouming,Liu Xinzhi,et al.Stability Analysis for Uncertain Switched Neutral Systems with Discrete Time-varying Delay:A Delay-dependent Method[J].Mathematics and Computers in Simulation,2009,80(2):436-448.
[12]Zhu Qiao,Hu Guangda.Stability Analysis for Uncertain Nonlinear Time-delay Systems with Quasi-one-sided Lipschitz Condition[J].Acta Automatica Sinica,2009,35(7):1006-1009.
[13]Qu Yan,Liu Hongyang,Si Yulin,et al.Stability Analysis of Discrete-time Stochastic Neural Networks with Time-varying Delays[J].Neurocomputing,2010,73(4/6):740-748.
[14]Lam J,Gao Huijun,Wang Changhong.Stability Analysis for Continuous Systems with Two Additive Time-varying Delay Components[J].Systems & Control Letters,2007,56(1):16-24.
[15]王述成,陈章位.基于多分辨谱分析的正弦加随机振动试验控制算法的研究[J].中国机械工程,2005,16(15):1335-1338.Wang ShuCheng,Chen ZhangWei.A New Algorithm for Sine on Random Vibration Test Based on Multirate Spectrum Estimation[J].China Mechanical Engineering.2005,16(15):1335-1338.
[16]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2):131-135.Zhong Wanxie.On Precise Time-integration Method for Structural Dynamics[J].Journal of Dalian University of Technology,1994,34(2):131-135.

