空间目标的数据处理研究

郭佳意， 钮俊清

（中国电子科技集团公司第38研究所，安徽 合肥230088）

1 导言

雷达对空间目标的实时精确跟踪是目前雷达数据处理技术研究的热点问题之一。空间目标包括在轨工作航天器和空间碎片。目前可跟踪的空间目标已超过14000个［1］。空间目标在运行过程中受到地球引力、日月引力、大气阻尼、地球粘弹性体潮汐等大量摄动因素的影响，运动规律异常复杂［1］。随着人类航天活动的增加，利用雷达对其实现准确地实时跟踪，获取精确的目标位置和速度变得日益迫切。

通常，地面传感器能够实时探测到空间目标的大致 坐标和 速度，多篇文献［2，3，4，5］已 讨论采 用 不 同的空间目标运动模型，利用最小二乘法、扩展卡尔曼滤波法等算法对量测数据进行滤波，并分析了各算法的滤波精度。Vergez［3］等采用考虑日月引力、大气阻尼等摄动因素的卫星运动模型，讨论了一阶和二阶扩展卡尔曼滤波法的跟踪精度，发现二者精度基本一致；Dai［4］等人在二维条件下讨论了多个站点联合量测跟踪空间目标的问题；Jia［5］等人的卫星运动模型则考虑日月引力、太阳辐射压等因素，其研究发现扩展卡尔曼滤波能够快速收敛，卫星轨道预测距离误差约200米。

然而，目前卫星轨道跟踪滤波的讨论大多集中在天体测量学等领域，在雷达数据处理领域则鲜见研究。由于雷达的工作特点，需要采用费效比较好的算法，即计算量少且滤波精度高。为此，本文基于协议地球坐标系下的卫星运动模型［3］分析比较了雷达数据处理领域常用的三种算法，最小二乘法、扩展卡尔曼滤波法和不敏卡尔曼滤波法的性能。文章第二部分首先介绍了这三种不同的算法；接着，文章第三部分介绍了协议地球坐标系下的卫星运动模型，并以STK软件产生的卫星数据为真值，以Monto Carlo加噪实验模拟量测数据［6］；最后，基于卫星运动模型分别采用三种滤波算法对量测数据进行滤波，并分析比较各算法的性能优劣。其结果发现，最小二乘法并不适用于空间目标的实时跟踪；而扩展卡尔曼滤波法与不敏卡尔曼滤波法精度基本一致，但扩展卡尔曼滤波的计算速度大大快于后者，因此在对空间目标进行实时跟踪时更宜采用扩展卡尔曼滤波法。

2 算法介绍

2.1 最小二乘法

最小二乘法是最常用的估计算法之一。该算法无需对被统计对象的统计特性、运动规律等做出假定，计算量小，从而应用广泛。设量测与估计值x满足

其中，w（j）为量测噪声。k时刻参数x的最小二乘估计为使该时刻误差的平方和达到最小的x值，即

卫星的运动轨迹近似于圆形或椭圆形轨道，因此最小二乘法采用二次曲线拟合。

2.2 扩展卡尔曼滤波

扩展卡尔曼滤波（Extended Kalman Filter，EKF）是在卡尔曼滤波基础上发展而来的，用于处理非线性问题的滤波方法。通常，观察数据与目标动态参数间的关系是非线性的。EKF将非线性问题Taylor展开，再将其做为线性问题处理。本文讨论一阶EKF。

设非线性系统的状态方程为x＝F（x（t），u（t）），其中，过程噪声u（t）为零均值的白噪声，其方差为Q（t）。量测方程为y＝H（x（t））＋v（t），量测噪声v（t）也为零均值白噪声，其方差为R（t）。过程噪声与量测噪声彼此互不相关。

扩展卡尔曼滤波具有递推形式，适合实时处理。若假设的模型与真实模型较相符，系统的非线性程度较弱，滤波结果随着时间推移就会与真值逐渐接近。

2.3 不敏卡尔曼滤波

非线性因子的存在往往会影响EKF的滤波精度，严重时甚至会导致滤波发散。不敏卡尔曼滤波（Unscented Kalman Filter，UKF）可以较好地解决这一问题。该方法是在不敏变换的基础上提出的，首先选取一系列δ采样点以体现系统的均值和协方差，经非线性系统传递后，后验均值与方差能够精确到二阶。该算法适用性强，稳定性好，无需将非线性系统线性化。其滤波过程如下：

首先，计算第k时间步目标状态的δ采样点：

各采样点相应的权重为

UKF适合各种非线性系统，稳定性好。若假设的模型与真实模型较相符，滤波结果随着时间推移就会与真值逐渐接近。

3 空间目标运动方程

本文采用地球协议坐标下的卫星运动方程［6］，即仅考虑地球中心引力、地球非球形引力J2摄动，日月引力等摄动因素，运动方程如下

4 仿真实验

4.1 仿真场景

利用STK软件模拟卫星目标轨迹并将该数据作为真值，如图1所示。其中，雷达位置经纬度为（108.558°，32.4231°）。蓝色曲线为卫星轨道，红色表示其中卫星被雷达跟踪的轨迹部分。

卫星轨道高度为1162km，速度7.266km／s。雷达数据采样率1s，跟踪点数100个。

为了比较三种算法的滤波精度，文中利用Monte Carlo加噪实验。在相同的条件下，分别采用三种算法对同一目标进行跟踪。设雷达的距离精度 150m，方位角精度0.15°，仰角精度 0.15°。Monte Carlo加噪次数分别为1000次，再分别统计各滤波结果的位置、速度的均方根误差σ＝（N为Monte Carlo实验次数）。

由于卫星的运动方程和真值都是建立在ECEF坐标系中的，而传感器测得的是站心极坐标系中目标的距离、方位角与仰角，即

其中，（xk，yk，zk）为传感器第k时刻测得的目标在站心直角坐标系中的位置坐标。因此在加噪时，首先应将真值数据转换到站心极坐标系中，再分别对距离、方位和仰角进行加噪。

图1 仿真场景

4.2 最小二乘法

首先采用最小二乘法对量测数据进行滤波。拟合时首先需要将量测数据从站心极坐标系转换到站心直角坐标系中，接着在x，y，z方向上分别采用二次函数进行拟合。将拟合结果与真值比较，空间位置和速度均方根误差分别如图2（a－c）所示。

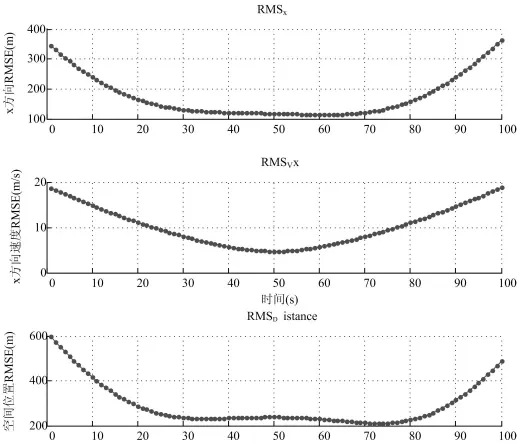
图2 最小二乘法拟合结果图

从图中可见，最小二乘法的拟合效果并不理想，其拟合精度在中心点处最小，越往头尾两端精度越差。由于拟合并没有考虑卫星真实的运动规律，仅仅将卫星轨迹近似于二次曲线进行处理，从而产生较大误差，短时间内即偏离真实的卫星轨道。

显然，最小二乘法的跟踪精度较差，难以用于空间目标的跟踪。故最小二乘法通常用于事后分析，而采用EKF和UKF进行数据的实时分析。

4.3 扩展卡尔曼滤波和不敏卡尔曼滤波

接下来比较一阶扩展卡尔曼滤波和不敏卡尔曼滤波的精度。目标的起始状态估计通过最初两个采样点获得，即

相应的状态估计协方差［8］为

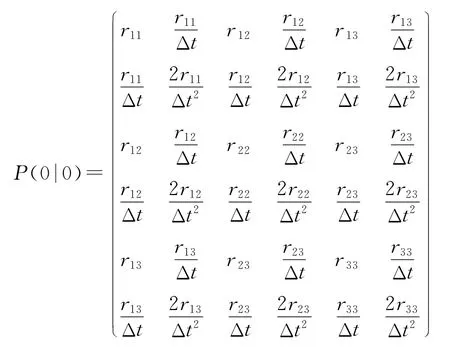
其中，rij取值如下式所示

在相同的条件下分别利用EKF和UKF对同一目标进行跟踪滤波，并比较二者的跟踪结果，其中EKF采用一阶模型。图3比较了由两种算法得到的x方向上位置、速度以及空间位置误差的均方差（RMSE）。图中，绿色表示量测误差，红色为扩展卡尔曼滤波后的均方差，蓝色为不敏卡尔曼滤波后的均方差。可以看出，在60点时，两种算法都已收敛，且滤波精度基本一致。

通常，由于EKF算法用Taylor展开将非线性问题转化为线性问题处理，非线性因子的存在往往会影响滤波的精度。然而，在本文中处理空间目标问题时，UKF的跟踪精度与EKF的精度差别很小，这是由于体系的非线性强度较弱造成：该目标的运行速度为7.27km／s，轨道半径为1162km，100s内划过角度仅为0.55°，目标的运行轨迹近似于直线，非线性很弱，因此UKF和EKF滤波精度基本一致。

此外，比较EKF和UKF算法的计算量。两种算法各计算1000次，每次100个时间步，统计所消耗的时间如表1所示，可见UKF是EKF所需时间的约5.8倍。

图3 EKF与UKF滤波结果比较图

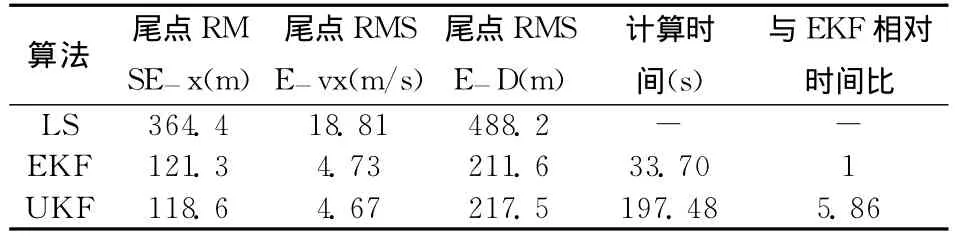
表1 三种算法性能比较表

综上所述，最小二乘法是一种常用算法，计算需求小，不需要统计假设，但与其它两种算法相比精度较差，拟合结果偏离真实的目标轨道，并不适合空间目标的跟踪滤波；空间目标运动由于其非线性不强，可以采用EKF算法，该算法适用于弱非线性系统和高斯噪声环境，且计算时间较短，能够满足雷达实时跟踪空间目标的要求；UKF滤波精度与EKF相比基本一致，但计算时间是EKF算法的约6倍。

5 结论

本文针对空间目标的跟踪滤波问题介绍了协议地球坐标系下的运动方程，及各种参数的估计算法。并通过仿真实验比较了三种不同的滤波方法的精度和性能。

空间目标运动速度快，轨道半径长，相对于地面上的某点在短时间内其运行轨迹近似于直线，非线性程度较弱。最小二乘法做为常用方法，虽无需目标的运动方程及噪声环境，但其跟踪精度较差。一阶扩展卡尔曼滤波法通过求解雅克比矩阵将非线性问题转化为线性问题处理，其跟踪精度较好，在100点时，空间位置均方误差下降至207.5米，且计算速度最快。不敏卡尔曼滤波适用于各种非线性系统，采用δ采样点，其稳定性好，滤波精度高。但由于空间目标运动非线性较弱，UKF的滤波精度与EKF基本一致。此外，UKF计算量较大。因此，EKF更适合空间目标的滤波跟踪。

［1］吴连大.人造卫星与空间碎片的轨道和探测［M］.中国科学技术出版社，2011年9月第一版.

［2］D.Hobbs and P.Bohn，Precise Orbit Determination for Low Earth Orbit Satellites［J］，MCFA Annals Volume 4，Vol.4，2006.

［3］P Vergez，L Sauter，and S Dahlke，July—September 2004.An Improved Kalman Filter for Satellite Orbit Predictions［J］，The Journal of the AstronauKcal Sciences，Vol.52，No.3.

［4］R Dai，U Lee，M Mesbahi.Distributed Orbit Determination Via Estimation Consensus ［J］. Spaceflight Mechanics，2011，140.

［5］P.Jia and Y.Xiong，An Orbit Determination Algorithm with Onboard GPS using Kalman Filter［J］，ACTA ASTRONOM ICA SINICA，vol.46，pp.441－251，2005.

［6］陈松明，基于STK的空间目标监视雷达系统设计研究［M］，西安电子科技大学，2010年硕士论文.

［7］焦文海，吴显兵，何涛.协议地球坐标系下的卫星运动模型［J］，测绘科学与工程，2004（3）.

［8］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.电子工业出版社，2009年7月第二版.