曲 波 域 经 验 Wiener 滤 波

李 伟, 杨 航

(1. 吉林大学 数学学院, 长春 130012; 2. 中国科学院 长春光学精密机械与物理研究所, 长春 130033)

去除观测图像中由于测量误差而产生的噪声是图像处理中的重要问题. 图像去噪方法主要分为空域法和变换域法两类, 传统的滤波方法属于前者, 如均值滤波、 ROF模型和双边滤波等. 在变换域去噪方法中, 小波变换因其具有时频局部特性和多分辨率特性, 已被广泛应用于各种图像去噪处理中. 小波变换通常对图像中的点奇异性表示较好, 但对边缘、 纹理等信息表达能力有限, 不能对其进行稀疏表达, 进而影响了去噪效果. 为了克服小波变换的局限性, 人们提出了曲波图像表示方法, 该方法对图像边缘信息的表达比传统的小波更有效. 曲波收缩是一个利用曲波变换能力得到图像估计的技术. 虽然曲波收缩方法一般优于其他图像去噪方法, 但大部分收缩去噪方法却仅使用简单的固定阈值. 在小波去噪方法中, 基于经验Wiener滤波(WWF)方法是一种改进的去噪方法, 它可以对每个小波系数采用Wiener估计, 从而改善小波硬阈值的均方误差(MSE)性能. 本文把Ghael的思想扩展到曲波域中. 与WWF不同, 为减少振铃效应和保留边缘, 先使用全变差(TV)估计设计Wiener滤波, 而TV模型可以通过使用分裂Bregman迭代算法得到有效解决, 然后使用曲波域的Wiener滤波估计图像. 实验结果表明, 该算法能获得更高的峰值信噪比(PSNR).

1 曲波变换

曲波由平移低通尺度函数和各项异性伸缩、 平移、 旋转的带通曲波函数构成. 与小波基函数[1]不同, 每个带通曲波基函数的支撑区间都满足宽度～长度2, 这种关系称为各项异性尺度关系[2]. 曲波变换图像去噪方法的基本原理是图像经过曲波变换, 噪声信息在曲波域中一般表现为绝对值较小的曲波系数, 通过某种规则确定某个阈值判断噪声和信号, 从而实现曲波变换图像去噪. 曲波不仅具有多尺度特性, 还引入了一个方向参量. 所以对于具有光滑奇异性曲线的目标函数, 例如边缘、 轮廓等特征, 曲波提供了稳定、 高效的和近乎最优的表示. 对于C2/C2空间的图像(具有分段光滑边界的分段光滑图像), 曲波能够提供最优的表示[2].

曲波变换[3]分为第一代和第二代两类. 第一代曲波变换的构造思想是通过尽可能小的分块将曲线近似到每个分块中的直线上, 然后利用局部Ridgelet变换分析其特性. 第二代曲波变换建立在频率域上, 实现过程无需用Ridgelet变换, 其曲波系数可以通过局部傅里叶基变换得到. 由曲波变换理论可知, 图像信号对应于相对较大的曲波系数, 噪声对应于相对较小的曲波系数, 所以可以选择合适的阈值, 做到保留较大的曲波系数、 舍弃较小的曲波系数, 实现含噪图像的去噪处理.

本文使用实现更简单的二代离散曲波变换[2]. 用μ表示一个三维索引(j,l,k), 其中j,l和k=(k1,k2)∈Z2分别表示尺度、 方向和平移参数. 曲波的定义如下: 令x∈R2,

其中

θl=2π·2-[j/2]·l,l=0,1,2,…,

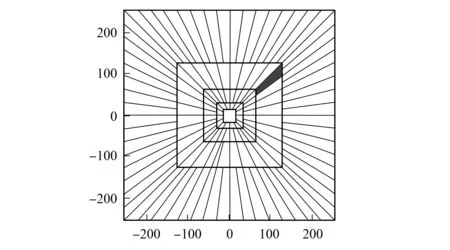
图1 离散曲波变换频域区域分割Fig.1 Region segmentation of discrete curvelet transform frequency-domain

其中径向窗W(如Meyer小波窗)分离频率域到|x|∈[2j,2j+1), 角度窗口V分离环形到楔形θl, 如图1所示. 在频域定义曲波

应用Plancherel定理, 可得

对于N×N的图像, 曲波变换及其逆变换都具有相同的计算复杂度O(N2logN).

2 Wiener滤波器

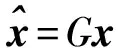
GW=Rx(Rx+σ2I)-1,

其中:Rx=E(xxT);I为单位矩阵;σ2为一个很小且不为零的数.Rx的特征展开式表示为

式中:N1为矩阵Rx的秩, 且N1

(1)

其中

3 曲波域经验Wiener滤波

经典的图像去噪问题：

y=x+n,

(2)

其中:y是含噪声图像;x是真实图像;n是零均值方差为σ2的高斯白噪声. 去噪的目的是从y中估计出x. 在曲波域中, 方程(2)变为

sj,i(k)=θj,i(k)+εj,i(k),

(3)

其中sj,i(k),θj,i(k),εj,i(k)分别表示观测图像y、 无噪声图像x和噪声n在尺度j及方向l上的曲波系数.

本文使用的第二代曲波变换. 曲波收缩方法有两种: 硬阈值和软阈值. 本文在曲波域中使用Wiener滤波去除图像的噪音, Wiener滤波估计图像的曲波系数为

(4)

为了构造Wiener滤波, 必须先从噪声图像中估计出θj,i(k), 本文使用基于TV的方法[5]得到该估计值. 基于TV的方法可以保留边缘信息, 而且还可以减少振铃效应, 因此, 对设计滤波器很合适. TV扩散模型[6-7]是目前最成功的图像恢复工具之一:

(5)

(6)

综上, 去噪算法步骤如下：

3) 通过计算曲波系数重建去噪图像.

4 实验结果

为了验证曲波域经验Wiener滤波方法, 下面进行几组实验. 分别在“Lena”,“Cameraman”,“Barbara”和“Pepper”图像上进行实验, 并与曲波收缩算法[9]和基于TV模型的方法(分裂Bregman方法)[10]进行峰值信噪比(PSNR)的比较, 结果列于表1. 由表1可见, 本文方法在PSNR上要优于曲波硬阈值方法和基于TV模型的方法. 图2和图3分别为含噪的“Lena”图像和“Barbara”图像用不同方法的去噪结果. 其中,

表1 不同实验的PSNR对比结果(dB)

(A) σ=20噪声图像, PSNR=22.11 dB; (B) 基于TV模型的方法, PSNR=31.23 dB; (C) 曲波收缩(硬阈值), PSNR=30.89 dB; (D) 曲波域的经验Wiener滤波器, PSNR=32.42 dB.图2 Lena图像的去噪结果Fig.2 Denoising of Lena image

(A) σ=20噪声图像, PSNR=22.12 dB; (B) 基于TV模型的方法, PSNR=26.87 dB; (C) 曲波收缩(硬阈值), PSNR=28.75 dB; (D) 曲波域的经验Wiener滤波器, PSNR=29.51 dB.图3 Barbara图像的去噪结果Fig.3 Denoising of Barbara image

综上可见, 本文提出了一种基于经验Wiener滤波的曲波去噪算法, 基本思路是通过由ROF模型获得的估计图像设计Wiener滤波. ROF模型可以通过分裂Bregman迭代快速解决, 使用曲波域中Wiener滤波去除含噪图像的噪声. 实验结果表明, 该算法优于已有的相关算法.

[1] Donoho D L, Jonestone I M. Adapting to Unknown Smoothness via Wavelet Shrinkage [J]. J Am Stat Assoc, 1995, 90: 1200-1224.

[2] Candes E J, Demanet L, Donoho D L, et al. Fast Discrete Curvelet Transform [J]. Multiscale Modeling & Simulation, 2006, 5(3): 861-899.

[3] Candes E J, Donoho D L. Curvelets: A Surprisingly Effective Non-adaptiverep Resentation for Objects with Edges [R/OL]. http://www.stat.stanford.edu/～candes/papers/curvelet-smstyle.pdf.

[4] Mallat S. A Wavelet Tour of Signal Processing [M]. San Diego: Academic Press, 1998.

[5] Rudin L, Osher S, Fatemi E. Nonlinear Total Variation Based Noise Removal Algorithms [J]. Physica D, 1992, 60: 259-268.

[6] Gastal E S L, Oliveira M M. Domain Transform for Edge-Aware Image and Video Processing, ACM Transactions on Graphics [C]//Proceedings of SIGGRAPH. Vol.30. New York: ACM Press, 2011.

[7] Michailovich O V. An Iterative Shrinkage Approach to Total-Variation Image Restoration [J]. IEEE Trans Image Process, 2011, 20(5): 1281-1299.

[8] Goldstein T, Osher S. The Split Bregman Method forL1-Regularize Problems [J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343.

[9] Starck J L, Candès E J, Donoho D L. The Curvelet Transform for Imaging Denoising [J]. IEEE Trans Image Process, 2002, 11(6): 670-684.

[10] Ghael S, Sayeed M, Baraniuk R G. Improved Wavelet Denoising via Empirical Wiener Filtering [C]//Proc SPIE Technical Conference on Wavelet Applications in Signal Processing. San Diego: Academic Press, 1997.