上承式钢筋混凝土箱型肋拱空间仿真分析及应用
冯 威,柯亮亮,雷 丹
(西安公路研究院,陕西西安 710054)
箱型拱桥是在20世纪60年代由四川省公路勘测设计院在总结众多拱式桥梁设计、施工以及使用经验和教训的基础上创新的一种新桥型。该桥型在施工过程中刚度大、稳定性好,成桥后为箱形截面抗弯、抗扭刚度大,与其它截面相比有很大优势,迅速成为设计中经常采用的桥型之一[1]。但近年来国内对钢筋混凝土拱桥的应用和研究投入不大,其发展速度较慢。究其原因,一方面,在高等级公路特别是高速公路建设中,由于其结构未采用预应力体系,很多人认为耐久性不足因而受到排斥;另一方面,在对国内西南地区在役钢筋混凝土箱形拱桥进行调查分析时发现存在不同程度的病害。
我国西南、西北山区地形、地貌以山地、丘陵、黄土高原为主,在公路和铁路建设中,大跨径拱桥应用广泛,且跨径有增大化的趋势。而箱型肋拱桥因为自身的显著优点,在近几年得到迅速发展。其结构体系在横桥向采用两片或多片拱肋并通过横向连接形成整体结构,受力明确简单。但在设计中涉及到各片拱如何共同分担桥上荷载问题,即荷载横向分布问题。在过去拱桥设计中,一般将全部荷载均摊给各拱肋。研究发现,对于大跨径拱桥,这种近似做法不合理,偏差较大[2]。目前国内对箱型肋拱桥的荷载横向分布计算一般采用杠杆原理法,将桥面板视为横向支撑在纵梁上的简支梁,荷载按杠杆原理分配于各相邻纵梁,再通过立柱将荷载传递给箱型主拱肋。文献[3]在拱桥活载横向分配系数的计算中采用折减系数进行修正,拱顶的折减系数为0.9~1.0,四分点和拱脚的折减系数分别采用0.9和0.8,此方法是否适用于箱型肋拱桥待于深入试验分析。此外,近年来随着电子计算机技术而发展起来的有限法从研究有限大小的单元力学特性着手,构造位移函数,得到一组以结点位移为未知量的代数方程组,再通过材料变形协调条件得到结点处需求未知量的近似解。该法适用性强,应用范围广,可以处理应力分析中的非均质材料、各向异性材料、非线性应力—应变关系以及复杂边界条件等难题,且采用矩阵表达,便于编程[4-5]。
本文采用MIDAS/Civil对上承式钢筋混凝土双肋双箱拱桥建立空间有限元模型,进行仿真分析,并进行荷载试验对比分析。
1 工程概况
五斗大桥位于佛山市南海区平洲镇,全长784.3 6 m,宽9.6 m,单向2车道,其中主桥长229.82 m,桥型为三跨上承式箱型肋拱桥。桥跨布置为(56+80+56)m,箱肋拱轴系数为1.167,矢跨比均为1/7,箱肋采用三段预制吊装。主拱肋共2片,每片拱肋由2片箱肋组成,箱肋间填充混凝土,2片主拱肋在立柱位置横向联系,主桥边跨主拱肋高1.3 m,中跨主拱肋高1.5 m。主桥箱肋和系梁均采用40#混凝土,桥面板、立柱和盖梁均采用25#混凝土。引桥主梁采用30#混凝土。桥面车行道宽9 m,两边钢筋混凝土防撞栏杆各宽0.3 m。该桥于1999年竣工,设计荷载为汽车- 20级、挂-100;桥面宽度为0.3 m (防撞栏)+9.00 m(行车道)+0.3 m (防撞栏)。
2 有限元分析
主桥为边跨跨径56 m、中跨跨径80 m的混凝土连拱结构,采用Midas/Civil有限元软件建立空间有限元计算模型进行计算分析。主拱圈、立柱、盖梁、横梁均采用空间梁单元模拟[6],桥面6 m现浇实心板和边中跨结合墩采用空间板单元模拟。模型中两侧边拱拱脚、结合墩墩底采用固结方式进行模拟,两侧端头处桥面板采用活动铰进行模拟,拱圈和立柱、拱圈和横梁、立柱和盖梁之间均采用刚接进行模拟,盖梁和桥面板之间采用两节点侧向和竖向变形耦合进行模拟。结合墩厚度取3 m,桥面实心板厚度取28 cm。主桥全桥共划为960个节点,937个单元。二期恒载作为节点荷载分布到桥面各节点上,试验荷载采用平面荷载加载方式,考虑车轮实际着地面积的影响。图1为五斗大桥有限元模型图。
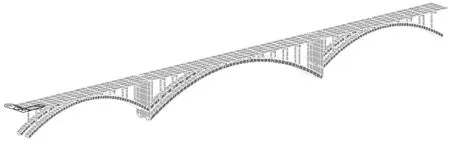
图1 五斗大桥有限元模型
3 试验加载
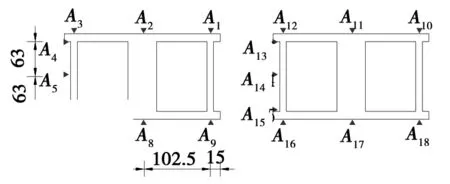
图2 五斗大桥应变测点布置
为验证分析效果、评定工程质量,对该桥进行荷载试验,采用空间直接加载方式。在此仅列出部分工况。工况①:80 m跨径拱桥最大负弯矩试验,控制截面为小里程侧拱脚,偏载;工况②:80 m跨径拱桥最大正弯矩试验,控制截面为拱顶,偏载。

图3 五斗大桥挠度测点布置
主桥应变测试截面选在试验跨拱脚及拱顶截面,采用振弦式应变计,测量各级荷载作用下的应变及卸载后残余应变。测点布置见图2,每个截面布置18个应变测点,应变测试精确到10-6。
主桥纵向挠度测点布置在距防撞墙根部5 cm处,分别布置拱脚、L/4、拱顶、3L/4、拱脚处,采用二等水准测量,测量精度要求达到0.1 mm,基准点设置在测试桥跨外。设置8个挠度测点,测点布置示意图如图3所示。实验采用4辆总质量34 t的三轴重车进行分级加载,标准轴重和轴距符合规范要求。
4 结果分析
按照加载程序进行上述2种工况试验,测试结果与相应工况有限元计算结果相对比,部分挠度观测结果见表1,应变测试结果见图4,5。

表1 工况Ⅰ挠度计算值与实测值对比表
注:校验系数=第3级实测挠度/第3级计算挠度。
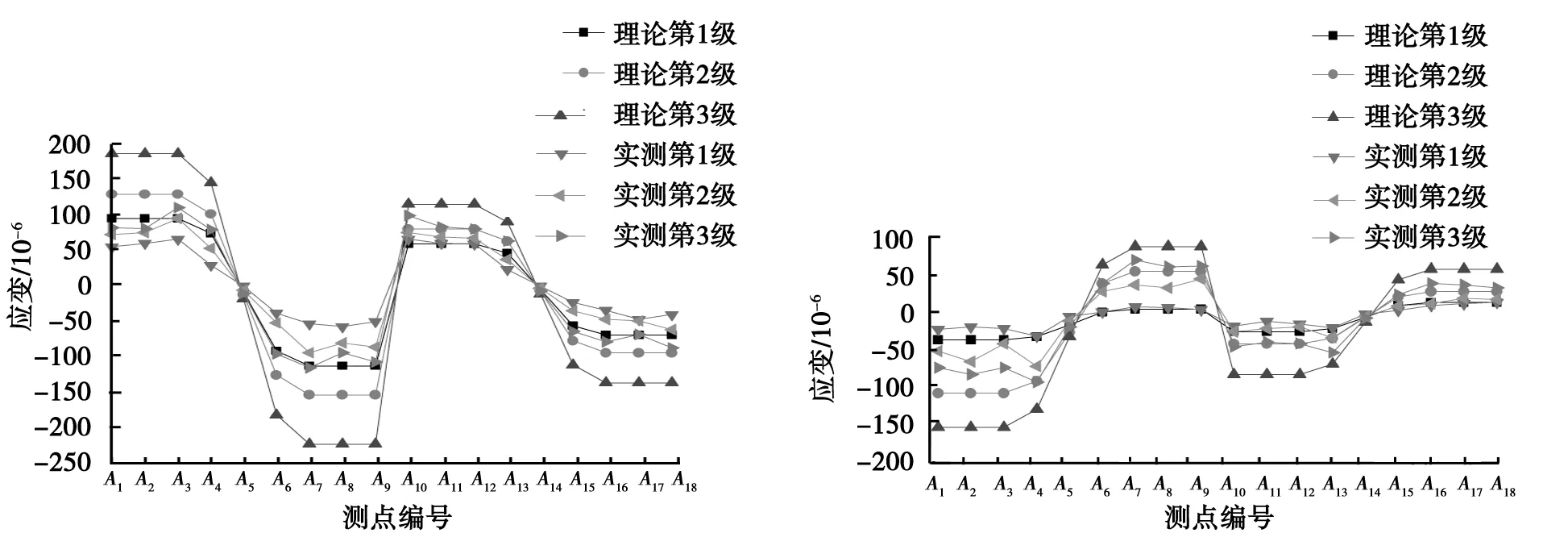
图4 工况Ⅰ应变比较图 图5 工况Ⅱ应变比较图
由表1可知,实测挠度与有限元计算挠度规律一致,实测挠度均小于计算挠度,校验系数为0.53~0.68,最大实测挠度为12.87 mm,远小于规范限值L/600=133 mm,说明该桥刚度满足设计及规范要求,同时说明本文的分析模型和分析方法是可行的。
由图4,5可知,测试应变与有限元分析应变规律一致,测试应变均小于计算应变,各工况校验系数均值为0.51~0.67,这与挠度测试结果一致,说明该桥的强度满足设计及规范要求,同时也再次说明本文的分析模型和分析方法可行。
5 横向载荷分布规律
双肋拱桥设计一般采用杠杆法分配荷载横向分布系数, 对于只有2片主梁的拱桥,这一方法精度足够高,可以满足工程实际的需要。桥面板可以看作是置于主梁上的悬臂梁,当荷载作用于悬臂时,该侧拱肋在该点反力的影响线竖标值>1,而另一侧为负值。然而实际情况是,荷载必须经过横梁传给另一侧拱肋,因此,结构实际的荷载分布要比杠杆法均匀的多[7]。
根据挠度计算和实测结果进行截面横向分布分析,根据测试截面理论(实测)的各测点挠度,理论(实测)荷载横向分布系数的计算式为
式中mi为试验荷载作用下,某一量测截面第i个测点的理论(实测)荷载横向分布系数;fi为试验荷载作用下,某一量测截面第i个测点的理论(实测)挠度;n为测点的个数。

表2 拱顶在工况Ⅱ的横向分布系数
拱顶在工况Ⅱ的横向分布系数对比见表2。由表2可知,结构的实测横向分布系数与理论计算结果接近,上部结构横向连接较好。
两拱肋杠杆原理法与空间有限元法计算偏载系数的结果见表3。由表3可以看出,杠杆原理法与空间有限元法计算结果存在较大差异,杠杆法计算的偏载系数结果远大于空间有限元法,为1.54,偏于安全,但过于保守、经济性差;而空间有限元法计算的偏载系数与实测结果吻合良好。因此建议引入修正系数λ对杠杆法计算荷载横向分布系数进行修正,对于偏载侧拱肋取λ=0.85;对于另一侧拱肋取λ=1.3,这样才能更好的反映结构的真实工作状态,指导设计工作。

表3 杠杆原理法与空间有限元法计算的拱肋偏载系数
注:Mcq为采用杠杆原理法计算的偏载系数;Mw为采用空间有限元法针对挠度计算的偏载系数;Mcm为采用空间有限元法针对应变计算的偏载系数。
6 结语
1)按空间梁和板壳单元建立了上承式钢筋混凝土双肋双箱拱桥的空间有限元分析模型,并以佛山五斗大桥为实例进行分析验证,其结果能够满足工程实际需要,精度较高,简洁、实用,为此类桥梁的进一步研究奠定了有限元基础;
2)数据分析发现,在荷载作用下,各截面的应变均很小,材料基本处于弹性阶段,卸载后残余值较小,说明结构弹性较好。结构强度、刚度、荷载横向分布和动力性能均满足正常运营使用要求;
3)大跨径轻型拱桥的横向应力分布不均匀,传统的杠杆法计算结果偏于安全,但过于保守,经济性差。建议引入修正系数λ进行修正,以便更好的反映结构的真实工作状态,指导设计工作。
参考文献:
[1]李国豪,石洞.公路桥梁荷载横向分布计算[M].北京:人民交通出版社, 1987.
[2]范立础.桥梁工程[M].北京:人民交通出版社, 1996.
[3]皇甫娟,钱永久,陈艳玮.拱桥荷载横向分布试验及分析[J].西南交通大学学报,2009(6):17-22.
[4]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001:15-24.
[5]戴公连,李德建. 桥梁结构空间分析方法与应用[M].北京:人民交通出版社, 2001.
[6]陈永顺,顾安邦.肋拱桥横向分布试验研究[J].重庆交通学院学报,1995(4):28-33
[7]向中福,王家林,张雪松,等.大跨径箱板拱桥荷载横向分布及其实用计算方法[J].重庆交通学院学报,2005,24(6):5-9,17.

