天桥人致振动性能评价研究

张 凯，周 燕，武 斌

(1.天津市赛英工程建设咨询管理有限公司，天津 300191；2.天津城建大学 土木工程学院，天津 300384; 3. 聊城市公路管理局 东昌府公路管理局，山东聊城 252000)

随着我国城市化的加快和交通量的增加，城市道路规划跨度逐渐加大，部分城市主干道红线宽度甚至达到上百m，设计为双向六车道，甚至达到10车道以上，当中央分隔带设计为隔离栏杆的形式时，就需要设计成大跨度的人行天桥。桥梁跨度较小时，结构的自振频率较大，远远避开人行走的步频，桥梁的人致振动问题并不明显，但当桥梁跨度加大，刚度下降，桥梁的自振频率降低，桥梁的自振频率接近人的步行频率，桥梁容易出现共振问题，振动带来的桥梁使用性、行走舒适性问题日益突出[1-5]。大跨度人行天桥的人致振动特性问题往往成为大跨度人行天桥设计的关键。

1 行人过桥的特点及避免人致共振的措施

人在桥上正常行走时，身体重心从一只脚转移到另外一只脚，呈Z字形。脚步的上下移动产生竖向激励荷载。除竖向力外，行人的双腿交替运动，导致人的重心左右摆动，因此也有横向力。由于行人重心每两步左右摆动一次，因此横向步行力的频率正好是竖向步行力的一半[6]。成年人正常行走时的步频为1.6～2.4 Hz，平均约为2 Hz，且均方差较小。因而竖向振动的主要频率为2，4，6 Hz等，横向激励的主要频率为1，2，3 Hz等[7-8]。从避免人桥共振的角度考虑，可以采用避开敏感频率法，尽量将桥梁的竖向自振频率避开一阶人行步频(1.6～2.4 Hz)，横向自振频率避开一阶人行步频(0.8～1.2 Hz)，人致共振的可能性会大大降低，从而保证桥梁的安全性和行人行走的舒适性。

文献[9]规定：为避免共振，减少行人不安全感，天桥上部结构竖向自振频率不应小于3 Hz。文献[10]建议避免人行桥的竖向振动固有频率为1.6～2.4 Hz和3.5～4.5 Hz。文献[11]则仅要求基频不应为1.5～2.3 Hz。文献[12]规定：当竖向振动基频>5 Hz时可不考虑人致振动问题，而对于≯5 Hz的桥梁结构，需要检算最大响应。

2 人行荷载的模拟

人行走过程中产生的激励荷载不但受到步频的影响，也受到人的体重、行走步幅等参数的影响，要准确确定激励荷载是很困难的。经过大量的统计实验，竖向激励荷载和侧向激励荷载可以近似用傅里叶级数表示[4-7]。

单人过桥竖向激励荷载Fv的计算式为

单人过桥横向激励荷载Fh的计算式为

式中G为单人的自重荷载，平均为600～700 N；fp为步行频率；αk为第k阶荷载谐波的动载因子，不同学者的研究结果差异较大；φk为第k阶荷载谐波的相位角。

研究表明，高阶谐波的动载因子迅速减小，一般只需考虑前三阶或前四阶谐波。

文献[12]提出单人行走的竖向激励荷载模型为

式中f0为桥面竖向一阶振动频率；G为单个行人的重量，取G=700 N；α为竖向荷载一阶谐波因子，取α=0.257。

人行步频偏安全的取桥梁竖向一阶自振频率，在桥梁阻尼较小时，将加大人桥共振的可能性。

文献[13]取单个行人重750 N ，竖向荷载一阶谐波因子为0.4，单人竖向激励荷载的计算式为

Fv=300sin(2πkf0t).

大跨度人行桥可以同时分布大量的行人，行人增加到一定数量后，会有部分行人的频率、相位非常接近，桥梁越长越宽，这一现象越显著。

文献[4-5]在研究日本户田公园人行斜拉桥时，通过实桥摄像机的跟踪统计结果，桥上同步行人数为0.2n(n为桥上行人总数)，则人群荷载的有效竖向力模型为

Fv=0.2n×294sin(2πkf0t).

文献[13]按照单人动力荷载乘同步系数cn给出同步时的人群荷载Ft(n)为

式中n可以根据桥上人行密度来确定，自由行走状态下桥上行人密度为0.3人/m2。

文献[14]规定人群荷载作用下的竖向激励为

Fv=k1k2sin(2πkf0t),

式中k1为人群密度为0.1人/m2条件下桥梁的人群影响系数；k2=150 N。

文献[12]假设以单人荷载过桥对桥梁的振动性能进行验算。文献[14]将人行荷载假定为一个固定的脉冲正弦荷载。文献[13]求解单人荷载作用下桥梁的振动响应时，将单个行人荷载作为集中荷载作用在容易引起最大响应的位置处。假定人的步幅为0.75 m，以0.75f0的速度在天桥上移动。上述几种荷载模式见表1。

表1 不同规范规定的等效人行荷载及其作用方式

注：B为桥梁宽度；L为桥梁长度。

3 天桥人致振动性能的评价指标

在人群不是特意齐步过桥，人群随意过桥情况下，行人过桥的桥梁安全性一般是有保证的。即使行人的步行频率和桥梁无活载情况下的基频一致，由于存在桥梁阻尼，桥梁的振幅不可能增大很多，而且振幅加大的情况下，行人会停下来或者快速离开桥梁，使人行激励频率自动调整。多数情况下，人行激励振动带来的是桥梁的使用性问题，振动使用性能评估主要通过人体舒适度指标来实现。

振动舒适度指标在铁路上研究的比较多，列车线路的质量和车辆性能评价常常要用到舒适性指标。我国铁路上常常采用Sperling 舒适度指标或者采用列车车体振动加速度指标，国外的铁路规范也有相应的舒适度指标[15]。

表2 人行桥的舒适度指标

文献[10]规定的人行天桥舒适度指标采用桥梁振动峰值加速度，竖向振动峰值加速度为0.7 m/s2，侧向振动为0.2 m/s2。

文献[1]给出的人行舒适度指标如表2所示。

文献[13]中用来表征舒适度指标不是峰值加速度,而是均方根加速度。

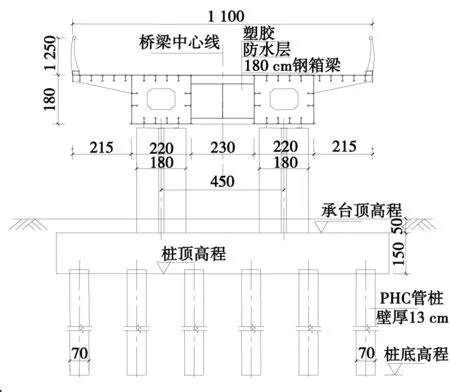
图1 天桥横断面图

4 工程实例

4.1 工程概况

工程位于某主干公路上，综合交通和规划意见，天桥设计跨径组合为(45+35+45)m，桥梁宽度为11 m，采用两箱室的钢梁截面形式，梁高2.0 m。桥墩采用钢筋混凝土矩形方墩，基础采用PHC群桩基础。支座采用板式橡胶支座，桥台位置设置D80伸缩缝。天桥的横断面如图1所示(图中长度单位为cm)。

4.2 桥梁结构形式对桥梁自振特性的影响

按照该梁高及截面尺寸比较不同结构体系对桥梁竖向弯曲自振特性的影响，如表3所示。

由表3可以看出，桥墩固结能提高桥梁的竖向自振频率，但墩柱刚度较小时，桥墩反而容易带动桥梁的竖弯。虽然中间两墩固结能显著提高桥梁的竖向弯曲频率，但是升降温度作用下墩底会产生很大的温度应力。综合比较，三跨连续梁方案的一阶竖向弯曲自振频率相对较大，结构上也比较容易实现，属于比较合适的方案。

对于桥梁的侧向振动问题，本桥的宽跨比较大，一阶侧弯频率>5 Hz，和横向人行激励频率相差较大，因而不控制侧向振动设计。

4.3 动力响应计算及评价

从表3可以看出，桥梁的竖向弯曲频率与人行频率接近，不满足3 Hz的规范要求[9]，即使加大梁高勉强提高到3 Hz，也与人行步频差别不大，仍有人致共振的可能。为此，必须进行天桥的动力响应评价研究。分别按照文献[12-14]给定的人行荷载和动力响应计算方法进行天桥的动力响应及舒适度评价，结果如表4所示。

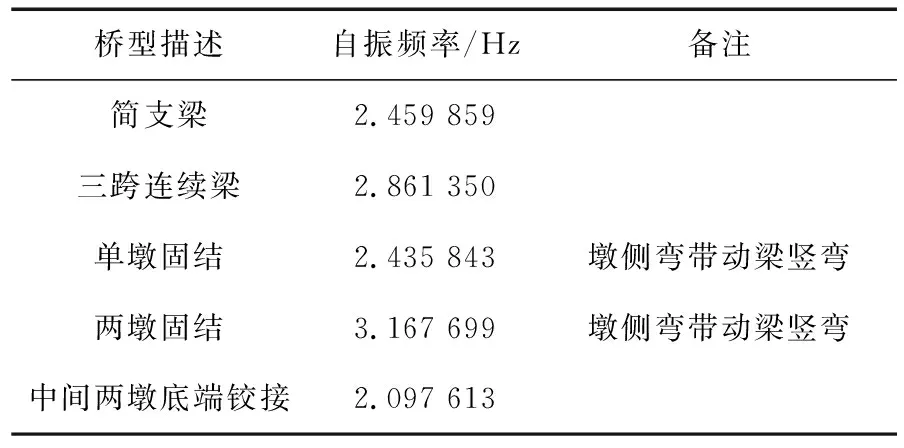
表3 不同结构体系对天桥自振频率的影响

从表4可以看出，按照不同规范计算得到的桥梁跨中最大加速度差别较大，其中按文献[14]计算的动力响应最大。但这3种规范评价该天桥均能满足规范的要求，桥梁的安全性和舒适性评价指标表明该桥处于舒适度为“最好的状态”。因而，对于大跨径天桥，除了从自振频率的角度进行安全舒适性评价外，开展动力响应评价具有更重要意义。

表4 天桥的舒适度评价结果

5 结语

大跨度人行天桥结构轻柔，自振频率较低，一般很难满足规范要求，当频率调整法不能达到设计规范的要求时，开展动力响应分析评价更有价值。

结合国内外学者研究成果和规范，本文给出了人行天桥人致振动响应的计算和天桥舒适性的评价方法，该方法计算简单，可以广泛应用于我国大跨径天桥人致振动性能的评价。

参考文献：

[1]陈政青.人行桥的人致振动理论与动力设计[J].工程力学,2009,26(2):148-158.

[2]梁炜.太原市汾河跻汾人行桥减震设计研究[J].城市道桥与防洪，2012,8(8):198-202.

[3]法永生.人行桥随机人行荷载作用下的振动分析及其舒适度评价的新方法[J].振动与冲击，2008，27(1):119-123.

[4]肖学双.钢结构人行桥人致振动舒适度及其控制研究[D].长沙：长沙理工大学,2009.

[5]伍定一.TMD对钢结构人行天桥的振动控制研究[D].长沙：长沙理工大学,2007.

[6]袁旭斌.人行桥人致振动特性研究[D].上海：同济大学,2006.

[7]康孝先.人致动力响应分析及在某曲线斜拉桥中的应用[J].湖南交通科技,2012,38(2):60-62.

[8]孙利民.人行桥人行激励振动及设计方法[J].同济大学学报：自然科学版，2004,32(8):996-999.

[9]北京市市政工程设计院.CJJ69—95城市人行天桥与人行地道技术规范[S].北京：中国建筑工业出版社，1996.

[10]European Committee for Standardization. EN1990：2002 Eurocode —Basis of Structural Design[S]. Belgium:European Committee for Standardization, 2002.

[11]日本道路協会. 日本道路協会 S54.1 立体横断施設技術基準.同解説[S]. Japan:日本道路協会, 1979.

[12]British Standards Association. BSI5400 Steel, Concrete and Composite Bridges Part 2: Specification for Loads[S]. London, UK: British Standards Association ,1978.

[13]International Standardization Organization. ISO/CD 10137 Bases for Design of Structures Serviceability of Buildings and Pedestrian Walkways Against Vibration[S].Geneva, Swaziland: International Standardization Organization, 2005.

[15]夏禾.车辆与结构动力相互作用[M].北京:科学出版社，2002.