基于灰色PSO-BP的客运量预测模型

张 忍，吕光辉

(长安大学汽车学院，陕西西安 710064)

公路客运量是反映运输业为国民经济和人民生活服务的数量指标。公路客运预测是交通规划的重要内容。目前常用的定量预测方法有回归分析预测、时间序列预测、灰色系统预测、马尔可夫链法、蒙特卡罗法等[1]。回归分析法的计算量大, 特别是非线性回归模型的求解比较困难；时间序列预测法不能反映事物的内在关系, 也不能分析2个因素的相关关系, 准确度差，只能适用于短期预测；马尔可夫链预测模型的关键在于转移概率矩阵的可靠性,该预测模型要求有足够准确的统计数据,才能保证预测精度[2]；蒙特卡罗法在预测过程中一般要假设某一频率分部的概率,这与现实有一定差距；灰色系统预测方法所需资料少以及收集资料所花费的时间和费用都少,缺点是预测精度不高。近年来已经有学者把神经网络与粒子群优化算法引入到预测领域。本文结合灰色系统思想与神经网络和粒子群优化算法的优点建立基于灰色PSO-BP(神经网络的粒子群优化算法)客运量预测模型，进一步提高预测精度。

1 预测模型及算法

1.1 灰色预测模型

灰色系统理论以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行规律的正确认识和有效控制[3]。GM(1，1)模型是灰色预测的核心， 其离散时间响应函数近似呈指数规律。设原始时间序列为

X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n)).

用1-AGO对序列进行一阶累加，生成序列

X(1)=(x(1)(1)，x(1)(2)，… ，x(1)(n))，

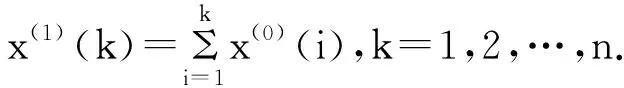
令Z(1)为X(1)的紧邻均值(MEAN)生成序列

Z(1)=(z(1)(2)，z(1)(3)，…z(1)(n))，

Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，

定义GM(1，1)的灰色微分方程模型为

x(0)(k)+az(1)(k)=b，

(1)

式中 a为发展系数，b为灰色作用量。

则灰微分方程的最小二乘估计参数列满足

式(1)的时间响应序列为

取x(1)(0)=x(0)(1) ，则有

灰色预测方程为

1.2 标准粒子群优化算法

标准粒子群算法(PSO)是一种有效的全局寻优算法，是基于群体智能理论的优化算法，通过群体中粒子间的合作和竞争产生的群体智能指导优化搜索。PSO保留了基于种群的全局搜索策略，将个体看作是在n维搜索空间中没有重量和体积的微粒，并在搜索空间中以一定的速度飞行。[4]在每次迭代中，每个个体(微粒)调整其飞行速度和位置的计算式为

vij(t+1)=wvij(t)+c1r1j(pij(t)-xij(t))+ c2r2j(pij(t)-xij(t))，

xij(t+1)= xij(t)+vij(t+1)，

式中 ij表示第i个粒子的第j维；t表示第t代；c1，c2为加速常数；r1，r2为随机变量；v为粒子的飞行速度；w为惯性权重；x为粒子；p为粒子经历过的最好位置。

1.3 BP神经网络预测原理

图1 BP神经网络基本结构

简单的BP神经网络主要由输入层、隐含层、输出层组成。其中，隐含层可以有多层，各层神经元之间通过连接权重相连接。BP算法中各层神经元的转移函数主要采用的是S型非线性函数。BP算法的基本思路是：输入信号从输入层经隐含层的函数作用后到达输出层得到输出信号，若实际输出的信号与期望值不符，网络进行反向传播，反复修正各层间的权值和阈值，直到得出的期望输出最小，即网络全局误差最小。其基本结构如图1所示。

BP神经网络模型的优点是短期预测精度很高，具有局部逼近网络的特点，可以近似任何非线性函数，不足之处是需要较为全面、能代表各种情况的样本数据,否则训练出来的神经网络外延性很差。

2 基于灰色PSO-BP预测模型的构建

1)PSO-BP神经网络的构建。将PSO优化算法与BP神经网络结合起来形成一种新的混合算法(即PSO-BP算法)。将神经元之间所有的连接权值编码成实数向量用来表示种群中的个体，随机生成这些向量的群体，按照算法步骤迭代。迭代中新生成的个体向量还原成神经网络权值，计算所有样本通过神经网络产生的均方差，若小于系统指定的误差，则训练过程停止，否则继续进行，直到达到最大迭代次数为止。[5]

2)算法的实现。①确定网络的拓扑结构、初始化粒子位置及速度、确定粒子数和最大允许迭代步数；②以网络均方差作为适应度函数，计算各个粒子的适应度值；③比较并确定每个粒子的局部最优值及每一代粒子的全部最优值；④迭代达到最大次数或最小误差时，停止迭代，并输出对应的神经网络权值与连接结构；⑤否则更新每个粒子的位置和速度，转到步骤②。

3)模型构建原理。构建基于灰色理论和粒子群优化BP神经网络的灰色PSO-BP公路客运量预测模型，如图2所示。该模型将陕西省的GDP、人口数量、公路总长、铁路客运量4个主要指标分别用灰色模型进行拟合和预测，并将拟合值作为PSO-BP网络的输入样本对其进行训练，最后将各指标预测值输入训练好的网络仿真得到相应的公路客运量预测结果[6]。其中，神经网络输入、输出节点数分别为4和1，输出层采用purelin函数，隐含层节点数确定为10，激活函数用tansig函数，训练步数设为5 000，误差目标设为0.001。

图2 灰色PSO-BP公路客运量预测模型

4)模型算法步骤。利用灰色PSO-BP预测模型对公路客运量进行实例预测，具体过程如下：①将陕西省的GDP、人口数量、公路总长、铁路客运量4个指标的历史数据分别用灰色模型进行变维数拟合，找到最优维数并得到相应的拟合值pi(i=1，2，3，4)；②对拟合数据pi和陕西省公路客运量进行归一化处理，使所有数值落入(0，1)，并耦合生成PSO-BP网络的数据样本集(其中，输入样本为公路客运量影响指标X=[p1，p2，p3，p4]，目标样本为公路客运量T=[P])；③使用Matlab7工具箱函数，建立PSO-BP神经网络，将2/3样本集赋给网络输入层相应的节点，按照粒子群优化BP算法对网络进行训练，直至误差达到要求[7]；④用剩余1/3 样本集对PSO-BP神经网络进行检验、评价；⑤将灰色模型预测值作为网络输入，用第③步训练好的网络进行仿真，得到公路客运量的预测。

3 应用实例

3.1 模型检验

以2002年—2011年的历史数据为基础，分别采用单变量GM(1，1)、BP神经网络和灰色PSO-BP组合模型进行拟合，拟合结果如表1 所示。从表1可以看出，3种算法中由于灰色PSO-BP模型能够反映人口总量与其影响因素之间相互制约、相互促进的关系，其拟合结果比单变量GM(1，1)和BP神经网络模型精度有了明显的改善。

3.2 未来公路客运量预测

由于灰色PSO-BP公路客运量预测模型属于短序列预测，只适合中、短期的公路客运量预测。所以对2012年—2016年共5个时间序列点的陕西省公路客运量进行预测，分别为105 787，112 455，129 390，132 576，148 260万人。在2002年—2011年 灰色PSO-BP网络预测模型的建立过程中, 发现预测值拟合程度很高, 模型精度在97% 左右，平均相对误差为1.643%，客运量的预测值基本符合本地区经济、社会快速发展趋势, 故该模型满足要求。

表1 公路旅客运输量预测结果 万人

4 结论

将灰色理论和神经网络进行了有机结合，并利用粒子群算法优化BP神经网络的连接权向量和阈值，形成了灰色PSO-BP公路客运量预测模型。经过与既有实测客运量的比较，灰色PSO-BP模型的预测精度明显高于其它几种预测方法，实例验证了该预测模型的合理性和可行性。

参考文献：

[1]邓聚龙.灰预测与灰决策[M].武汉：华中科技大学出版社, 2002.

[2]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2010．

[3]刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2008：12.

[4]张长胜，孙吉贵，欧阳丹彤.一种自适应离散粒子群算法及其应用研究[J].电子学报，2009，37(2)：299-304.

[5]秦伟刚，黄琦兰．基于RBF神经网络的交通流预测[J].天津工业大学学报，2006，25(2)：71-73．

[6]沈家军,王炜,陈峻.基于灰色马尔可夫模型的近期公交客流量预测[J].公路交通科技, 2007, 24(9): 120-123.

[7]张德丰．MATLAB神经网络仿真与应用[M].北京：电子工业出版社，2009．