求解软硬时间窗共存配送路径问题的改进遗传算法

史 昊，何俊生，马 畅

(重庆交通大学交通运输学院，重庆 400074)

现实中的配送客户往往会提出期望的收货时间区间，要求配送车辆在这期间到达。按对送达时间要求的严格程度不同，时间窗分为软时间窗和硬时间窗。近年来，有关软时间窗或带硬时间窗的软时间窗车辆路径问题的研究较多[1]，但对节点时间窗软硬不同且同时存在的情况的车辆路径问题的研究还比较少，而这种情况在现实的配送问题中时常出现。本文给出一种改进的遗传算法，对软硬时间窗共存配送路径问题进行求解，并与基本的遗传算法计算效果进行对比。

1 模型

1.1 问题描述

车辆从某固定的配送中心出发，给已知的配送服务节点进行配送。每个节点都要求一个已知固定配送服务时间窗。假设每个客户节点只由一辆车进行服务，且足以满足该节点对进货量的需求。所有节点(包括配送中心和客户节点)间距、每个配送点的需求量和服务时间、车辆的载重量及最大允许的行驶距离都为已知。在车辆配送过程中还要受到以下基本约束〔2-3〕：①车辆不允许超载；②车辆有最大行程限制；③时间窗限制。

本文研究在所有约束条件都满足的情况下，如何确定配送的路线方案，使目标成本最小。

1.2 建模

根据上述对问题的描述，做如下假设〔4-6〕：设配送中心共有n个服务节点，i,j表示节点的编号(i,j=1,2,3,…，n)，配送中心编号为0；每个节点的需求量为Pi，单车的最大装载量为p； 节点之间的距离dij，节点的服务时间为Ti；单车的单位行驶距离成本为c1，单车出车成本为c0；所用车辆数(路径数)为K，单车最大行驶距离为D；i节点时间窗为(ETi,ELi)，且ELi-ETi>Ti，若为软时间窗，惩罚函数为

cfi=eimax{ETi-tik,0,tik-(ELi-Ti)}，

式中cfi为软时间窗的惩罚函数在i点的值；tik为k车到达i节点的时间；ei为惩罚系数。

若为硬时间窗，惩罚函数则为

cfi′=max{ei′(ETi-tik),0,M[tik-(ELi-Ti)]}，

式中cfi′为硬时间窗的惩罚函数在i点的值；ei′为等待期间的惩罚系数；M为晚于硬时间窗的惩罚系数，为一个很大的正数。

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

ei≥0,ei′≥0,,i=1,2,3,…，n.

(8)

目标函数(1)分为3部分，分别为：①车辆未在时间窗要求时间段到达的惩罚值；②车辆行驶成本；③车辆的出车成本。约束条件中，式(2)表示每条线路上的节点货物需求总量小于车辆的最大载货量；式(3)表示车辆的运行距离不能超过允许的最大行驶距离；式(4)、(5)表示每辆车出发到各节点服务后，离开并最终回到起始的配送中心；式(6)、(7)表示每个配送节点有且只有一辆车通过；式(8)表示迟到或早到惩罚系数为一个非负数。

2 算法设计

2.1 编码

采用自然编码方式，若客户数为6个，则随机生成的一个染色体编码如[ 1，4，6，3，5，2，0 ]，其中0为配送中心，其它代表客户点，表示一种线路分配方案[7]。因为每个回路车辆最终要回到配送中心，路线首尾可添加配送中心0(下划线表示)，编码进一步调整为：[ 0，1，4，6，3，5，2，0，0 ]。所以这种方案的配送需要2辆车，2条配送回路为：0→1→4→6→3→5→2→0；0→0。但0→0又不能成为一条路线，则该染色体实际的解码意义为安排1辆车和1条配送路线。

根据上述解释，假设问题中可用最多车辆数K=4，即最多使用4辆车分4条线路进行配送。则可以在形成的排列中随机插K-2入个配送中心点0，比如：[0，1，4，0，6，0，3，5，2，0，0 ]。该染色体的解码后实际含义就为：仅派发3辆车， 3条配送回路分别为：0→1→4→0； 0→6→0； 0→3→5→2→0。

2.2 适应函数

这里以目标函数作为适应函数，个体对应的目标函数值即为此个体的适应值。

2.3 选择操作

采用轮盘赌的方式选择染色体复制到新种群，直到新种群规模与父代相同为止。

2.4 改进的交叉操作

从种群第一个染色体开始，两两成组，对每组染色体，在交叉概率Pc影响下，则取相邻染色体两端0不动，取中间随机一段进行交叉互换。

式中k1，k2，k3分别为0～1的小数。

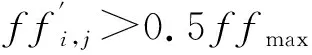
2.5 改进的变异操作

变异操作是对种群每一个染色体，在变异概率pm，随机取染色体2个数字并交换位置，形成新染色体。变异概率pm为

(9)

式中k4,k5为0～1的小数。

式(9)表明，当ffi

3 算例分析

C市某医药物流配送中心，担任所辖区域内14个客户的配送业务，各个客户的间距见表1，时间窗、惩罚系数等参数见表2。其中需要的配送车辆数待求，车辆的最大载荷为25，单车最大行驶距离为300，固定单车发车成本为150，单位运输成本为1。其它已知参数见表1、表2。

表1 各配送节点的间距(0为配送中心)

表2 客户节点各项参数

在CPU主频为2.0 GHz，内存2 GB的计算机上，分别采用基本遗传算法、改进遗传算法计算10次。算法中设置初始群体规模为40，M取10 000，遗传迭代次数genmax=1 000，基本遗传算法中交叉概率pc=0.6，变异概率pm=0.05；改进算法中k1，k2，k3，k4分别取0.01，0.05，0.1，0.1，0.01。两种方法计算最优成本分别为1 322.2和1 301.4，最优迭代过程见图1。

a)遗传算法

b)改进的遗传算法

图1 两种算法最优解的迭代变化过程对比

由图1可知，改进算法得到的最优解更优，迭代效率也更高。最终得到最优解为：[0 3 2 0 1 8 7 0 6 11 10 14 0 4 5 13 12 9 0 ]。即最优方案为：配送中心安排4辆车，配送线路分别为：0→3→2→0； 0→1→8→7→0； 0→6→11→10→14→0； 0→4→5→13→12→9→0。

4 结论

探讨了一种求解软硬时间窗共存下配送路径问题的改进遗传算法，建立了配送路径优化模型，设计了改进的交叉、变异准则，并用数值算例计算结果与基本遗传算法比较，结果证明本设计改进遗传算法的有效性，且比基本遗传算法更容易避免陷入局部最优解，迭代次数更少。

参考文献：

[1] éric Taillard, Philippe Badeau, Michel Gendreau, et al. A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows[J]. Transportation Science, 1997, 31:170-186.

[2]George Ioannou, Manolis Kritikos, Gregory Prastacos. A Problem Generator-Solver Heuristic for Vehicle Routing with Soft-Time Windows[J]. Omega，2003, 31(1): 41-53.

[3]Sun Guohua.Research on Open Vehicle Routing Problem with Full Load and Soft-Time Windows[J].Computer Engineering and Applications, 2011, 47(17):13-17.

[4]Jixian Xiao, Bing Lu.Vehicle Routing Problem with Soft Time Windows[J].Advances in Intelligent and Soft Computing, 2012, 168: 317-322.

[5]Z Fu, R Eglese , Y O Li. A Unified Tabu Search Algorithm for Vehicle Routing Problems with Soft Time Windows[J].Journal of the Operational Research Society, 2008 (59): 663-673.

[6]Brian Kallehauge. Formulations and Exact Algorithms for the Vehicle Routing Problem with Time Windows[J].Computers & Operations Research,2008, 35(7): 2307-2330.

[7]Tsung-sheng Chang, Yat-wah Wan, Wei Tsang OOI. A Stochastic Dynamic Traveling Salesman Problem with Hard Time Windows[J].European Journal of Operational Research, 2009, 198(3): 748-759.

[8]Hongtao Lei, Gilbert Laporte, Bo Guo. The Capacitated Vehicle Routing Problem with Stochastic Demands and Time Windows[J].Computers & Operations Research, 2011, 38(12): 1775-1783.

[9]J C Bean. Genetic Algorithms and Random Keys for Sequencing and Optimization[J].ORSA Journal on Computing, 1994, 6 (2): 154-160.

[10]乔均俭，王爱茹，周静. 带时间窗车辆路径问题的最优解[J].商场现代化，2007(2)：128-129.