地下厂房施工过程的三维非线性数值模拟分析

袁 帅，何蕴龙，曹学兴

(1.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072;2.中国五环工程有限公司，武汉 430223)

1 研究背景

地下厂房是处于复杂地质条件下的建筑工程，其围岩稳定性与天然地质环境、施工开挖方式及支护方式密切相关［1－2］。地下厂房的开挖在力学上可以认为是一个应力释放和回弹变形问题。1982年陈宗基［3－4］提出地下厂房所处岩体在未开挖时由于岩体自重、地质构造运动、地形地貌和剥蚀作用、地下水作用等因素存在着初始地应力场。地下厂房的开挖会使洞室边界裸露岩体的初始应力得到释放，并进一步引起岩体应力场和位移场的重新分布。开挖过程模拟的关键在于开挖释放荷载的计算，邓肯(J.M.Dancan)提出“反转应力释放法”［5］将围岩的初始状态应力与开挖荷载作用下的应力增量进行叠加［6－7］以计算释放荷载。支护理论则以新奥法为代表，该法要求尽可能地发挥围岩的“自承”作用、减少对围岩的破坏扰动，其优点是经济、快速、安全、适应性强以及减少开挖量和衬砌量，加快施工进度等［8］，喷锚支护是新奥法的主要支护措施，在地下洞室和隧道开挖工程中得到了广泛的应用。对于喷锚支护模拟中的关键问题，即如何模拟锚杆和围岩的联合作用，国内外开展了广泛的研究:目前主要采用隐式单元法［9－10］来模拟锚杆的支护效应，这种方法不会增加前处理工作，可以有效地反映锚杆的长度、密度、倾角对洞室开挖的影响而且较好地模拟锚固的时间施加效应。本文以隐式杆单元模拟锚杆，以壳单元模拟混凝土喷层，采用三维弹塑性有限元对冗各地下厂房洞室群进行模拟分析，研究在整个开挖过程中洞周围岩应力变形的分布规律、塑性区的发展规律、锚杆受力变化情况等。并针对计算结果对支护方案进行了优化，为工程设计和施工提供参考和依据。

2 工程概况及有限元模型

冗各水电站地下厂房洞室群主要由引水洞、主厂房、副厂房、集水井、中控室、尾水洞、交通洞等组成。主厂房长68.2 m、宽15 m、高37 m，与副厂房的净距 30 m，副厂房长41.6 m、宽13.4 m、高27.2 m。洞室群总体处于新鲜完整的灰岩岩体中，岩层单层厚度较大，厂房长轴方向与岩层走向交角大于65°，利于洞室稳定，边墙围岩类别主体为Ⅲ类。

根据工程施工组织设计主厂房分5层开挖，副厂房分4层开挖。在天然条件下地应力场的基础上三维弹塑性有限元计算主要模拟7个开挖载荷步，每步开挖完成后当围岩刚度消失50%时即进行相应的喷锚支护。采用单元生死技术对地下厂房洞室群施工开挖过程进行模拟其施工开挖方案见图1所示。

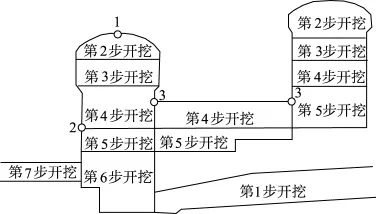
图1 地下厂房洞室群开挖载荷步示意图Fig.1 Load steps of the excavation of underground caverns

根据工程经验，地下洞室的开挖仅在洞周距洞室中心点3～5倍洞室开挖宽度(高度)的范围内存在影响［11］。有限元模型上游边界距离厂房上游边墙150 m，下游边界至尾水洞出口，铅直方向取4倍厂房高度，厂房轴线方向两边界距厂房70 m。无支护措施时，有限元模型共有节点60 453个、单元57 980个，加上支护措施后，模型共有节点103 435个、单元95 068个。y轴表示上、下游方向，指向下游为正，x轴表示厂房轴线方向，指向山内为正，z轴表示铅直方向，满足右手螺旋法则。由于计算区域顶部已取到山顶，上表面采用自由边界条件，上下游边界及厂房轴线方向边界施加法向约束，底部采用全约束。初始地应力考虑岩体的自重应力。主要洞室有限元网格如图2所示，主厂房的喷锚支护网格图如图3所示。岩体采用理想弹塑性模型进行计算，采用考虑剪切屈服与拉裂破坏相结合的Mohr-Coulomb屈服准则，锚杆和混凝土采用线弹性材料进行计算。材料计算参数见表1。

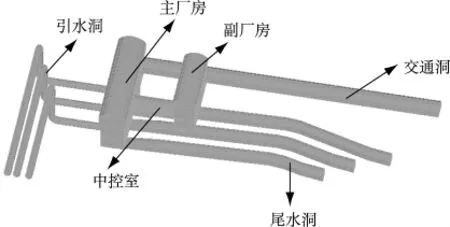
图2 主要洞室有限元网格Fig.2 Finite element meshes of main caverns

图3 主厂房喷锚支护网格Fig.3 Meshes of bolting support for the main powerhouse

3 计算成果及分析

选取主厂房顶拱中心(沿主厂房轴线方向)、上游边墙1/2墙高位置(沿主厂房轴线方向)及中控室顶拱中心位置(沿中控室轴线方向)的3条特征线(见图1)和贯穿主、副厂房、中控室顶拱中心以及引水洞、尾水洞的典型剖面，对洞室围岩的应力变形、塑性区的发展以及锚杆的受力情况进行研究。各方向应力示意图如图4所示。

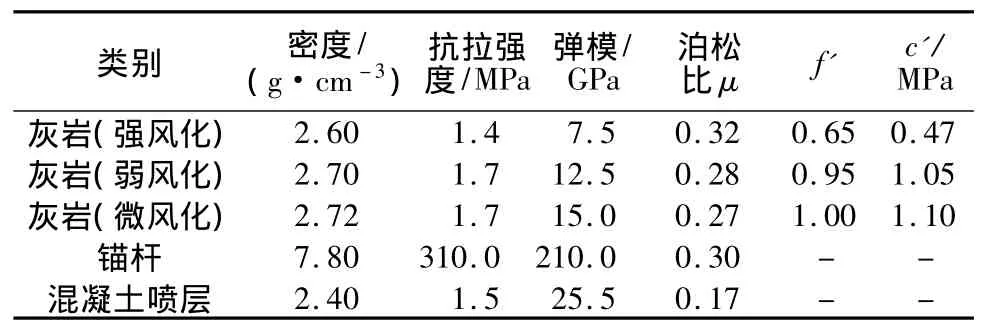
表1 计算材料力学参数Table 1 Mechanical parameters of the material for calculation

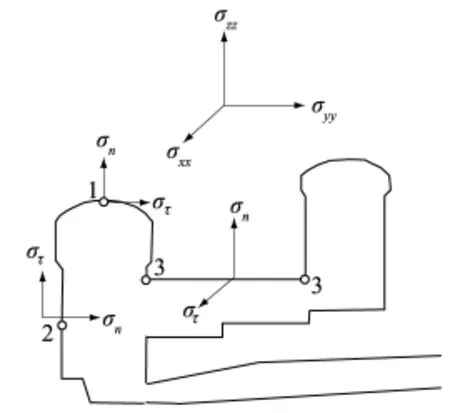
图4 应力方向示意图Fig.4 Stress directions

3.1 围岩变形

洞室围岩变形见图5至图7。从图5至图7可以看出:

(1)在开挖过程中，主厂房顶拱的两端受到未开挖岩体的约束，其沉降较小，其它部位沉降较大;开挖完成后，主厂房与交通洞交叉处有最大沉降4.2 mm。

(2)主厂房的上游侧墙中部由于处于第4步与第5步开挖的交界处，故第4步开挖完成后没有发生明显的变形，第5步和第6步开挖使其产生较大的向下游变形，第7步进水管的开挖对其变形基本没有影响。上游侧墙在开挖过程中主要发生向下游的变形，且上游侧墙中部向下游的变形大于两端的变形;开挖完成后最大变形值出现在主厂房上游边墙中部的位置，其最值为1.6 mm。

(3)第4步和第5步开挖对中控室顶拱向下的沉降影响较大，在第4步开挖完成后其顶拱接近副厂房的位置处由于受第5步待开挖岩体的约束作用，向下沉降值较小。开挖完成后，最大沉降值出现在顶拱中部附近，其值为3.3 mm。

在开挖过程中及开挖完成后，洞室主要发生向洞室内部收缩的变形;前期开挖主要影响主副厂房的顶拱部位围岩的变形，在后期的开挖中随着开挖面逐渐远离顶拱，对顶拱部位围岩位移影响较小。

3.2 围岩应力

图8给出了开挖过程中3条特征线上切向应力的分布曲线，从图中可以看出:

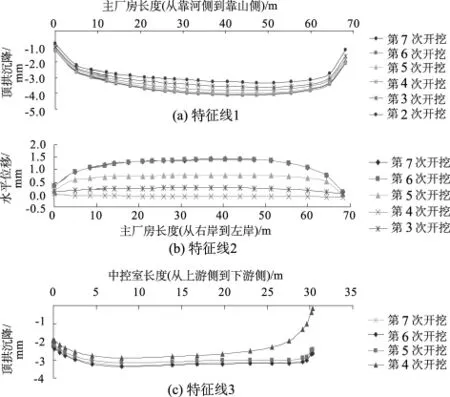
图5 位移变化曲线Fig.5 Curves of displacement variation

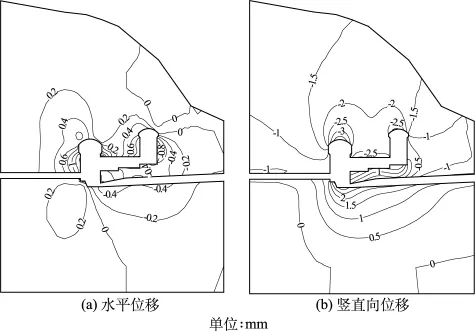
图6 开挖支护完成后的典型剖面位移分布图Fig.6 Displacement distribution of typical profile after bolting support

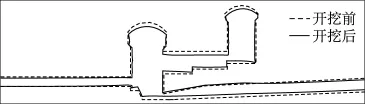
图7 开挖支护完成后的典型剖面变形示意图(放大500倍实线表示变形后轮廓)Fig.7 Deformation of typical profile after bolting support(magnified 500 times，solid line represents the shape after deformation)

(1)在第2步开挖完成后主厂房的顶拱处于低压应力状态，在第3步开挖完成以后顶拱两端处于受压状态，中间位置处于较小的受拉状态，第4步至开挖完成后顶拱处的切向应力基本上没有变化。

(2)在第4步开挖完成以后主厂房的上游侧墙中部处于受压状态，中间位置处的压应力大于两端，在第5步开挖完成以后上游侧墙中部处于低压状态，在第6步开挖完成以后上游侧墙中部中间位置处于低拉状态，在两端处于受压状态，第7步的开挖对于侧墙的切向应力分布基本上没有影响。

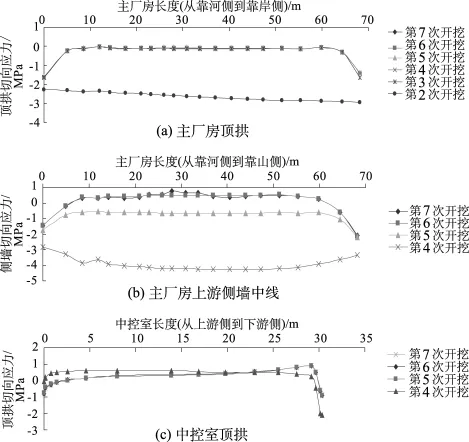
图8 切向应力(στ)变化曲线Fig.8 Curves of tangential stress(στ)variation

(3)在第4步开挖完成以后中控室顶拱靠近上游侧处于较小的拉应力状态，顶拱靠近副厂房附近由于受到未开挖岩体的约束作用而处于压应力状态;在第5步开挖完成以后中控室顶拱靠近上游侧处于压应力状态，靠近下游侧处于低拉状态。第6步、第7步的开挖对中控室的顶拱切向应力的分布基本上没有影响。

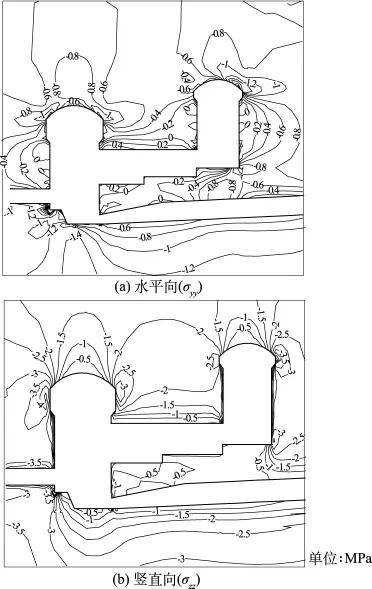
图9 开挖支护完成后的典型剖面正应力分布图Fig.9 Normal stress distribution in typical profile after bolting support

图9给出了洞室剖面水平向(σyy)和竖直向(σzz)正应力的分布图，由图可知:在开挖过程中，主要在洞室周边出现了拉应力或低压应力及较大的压应力区，在结构转折处出现了应力集中。开挖完成后，水平向正应力(σyy)，在主副厂房的上下游边墙及中控室的顶拱和底板都出现了拉应力，经过非线性计算部分区域围岩出现拉裂屈服，应力场调整后其最大拉应力值为0.43 MPa出现在中控室顶端靠近主厂房附近，在厂房顶拱存在较小的低压应力区。竖直向正应力(σzz)，主要在厂房顶拱、底板及中控室、尾水洞顶拱和底板出现低压应力区，并出现了一定的拉应力，调整后拉应力最大值为0.10 MPa，出现在中控室底板靠近副厂房附近;在厂房顶拱两端的转折处及进水口结构转折处出现了压应力集中，最大压应力为 －4.53 MPa。

3.3 围岩塑性区

从图10中围岩塑性区(黄色区域为拉裂屈服，紫色区域为剪切屈服)的分布及发展情况来看，第2步即厂房顶拱部分开挖完成后，主要在主厂房上下游边墙、尾水洞的底板及洞顶位置形成了较小面积的塑性区，塑性区的深度在1 m以内;第4步开挖完成后，主厂房上游边墙塑性区向内有所发展，在中控室顶拱表层出现塑性区;第6步开挖完成后，在中控室底板出现小面积的塑性区;开挖完成后，上游边墙塑性区有所扩展;在主副厂房上游边墙，中控室顶拱、底板，尾水洞底板等部分区域表层围岩出现塑性区。

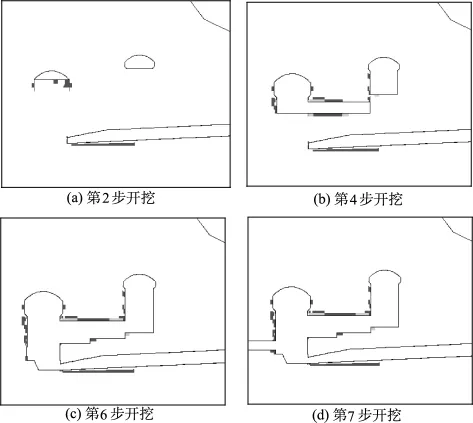
图10 施工过程中典型剖面塑性区分布Fig.10 Plastic zone distribution in typical profile during construction

3.4 支护锚杆受力状况分析

图11给出了在开挖过程中主副厂房顶拱处支护锚杆最大轴向应力的分布图，从图中可以看出:第2步开挖支护完成后，主厂房顶拱处支护锚杆最大应力为44 MPa，第2步至第5步开挖对顶拱处锚杆的应力影响较大，第6步及第7步对其影响较小。副厂房顶拱处支护锚杆最大轴向应力变化规律与主厂房顶拱处的一致，最大拉应力不超过36 MPa。图12给出了主副厂房典型剖面支护锚杆轴向应力分布图，从图中可以看出:开挖完成后锚杆基本上都处于受拉状态，厂房顶拱和上下游边墙中部由于围岩变形较大，锚杆拉应力较大，在主厂房顶拱有最大拉应力在45 MPa;锚杆应力从围岩表层向围岩深处呈递减趋势，在锚杆末端应力值最小。

图11 主副厂房顶拱处锚杆最大轴向应力分布Fig.11 Maximum axial stress distribution of anchor in the top arch of main and auxiliary powerhouse

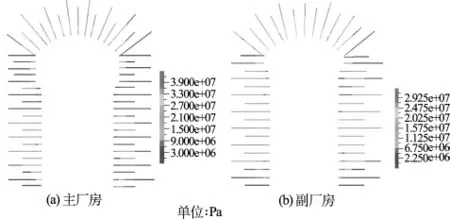
图12 主副厂房典型剖面锚杆轴向应力分布Fig.12 Axial stress distribution of anchor in the typical profile of main and auxiliary powerhouse

3.5 支护措施优化方案

通过前面的分析可知整个开挖过程中，洞周围岩位移变化规律正常，量值较小，塑性区主要分布在洞室周边，围岩稳定性较好。但在洞室交叉口处围岩的变形较大，出现较大范围的塑性区，为此提出支护措施优化方案:在交通洞和中控室靠近主厂房和副厂房边墙5 m范围内增加钢筋混凝土衬砌厚度，并将该区域的锚杆长度由原来的8 m和6 m相间布置加长为9 m和6 m相间布置;在主副厂房边墙与中控室和交通洞交叉处加密锚杆，布置间距由原来的1.5 m ×1.5 m加密为1.0 m ×1.0 m，具体的支护措施优化布置示意图如图13所示。

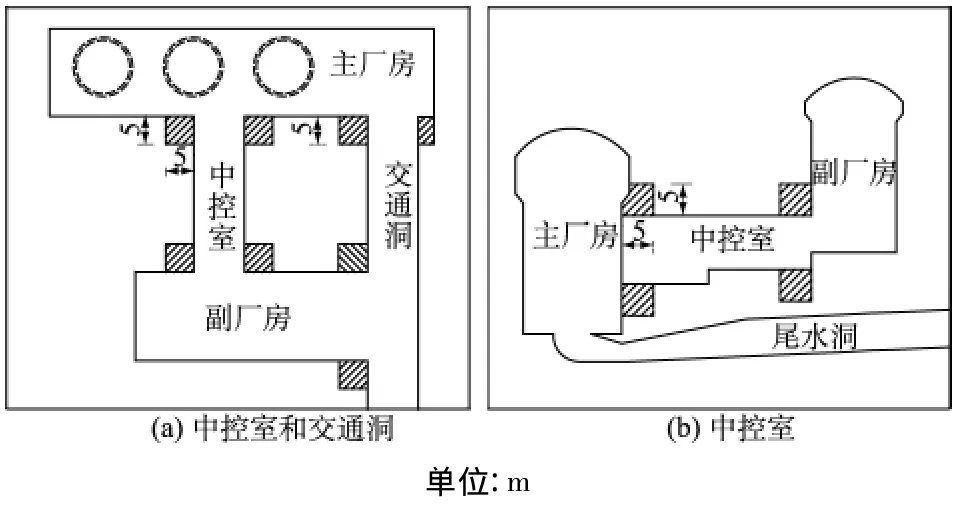
图13 支护措施优化方案(范围)示意图Fig.13 Schematic of the optimization of bolting support measure(area)

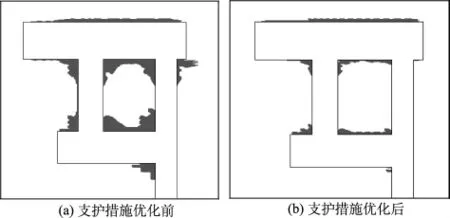
图14 支护措施优化前后塑性区分布示意图Fig.14 Plastic zone distribution before and after the bolting support optimization

图14给出了在支护措施优化前后主厂房1/2墙高处水平切面塑性区的变化情况。由图可以看出:在支护措施优化前主副厂房与交通洞、中控室交叉口处的塑性区深入围岩较深，范围较大;在支护措施优化后该区域的塑性区范围明显减小。支护措施的优化可以有效地抑制洞室交叉口处塑性区的发展，增强洞室围岩的整体稳定性。

4 结语

本文以隐式杆单元模拟锚杆，以壳单元模拟混凝土喷层，采用三维非线性有限元技术，对洞室群的开挖支护动态过程进行了模拟计算。主要得到以下结论:

(1)地下厂房在开挖过程中洞室主要发生内缩变形:洞室的顶拱下沉，底板向上回弹，边墙发生向洞室内变形，在洞室交叉口处变形较大。整个开挖过程中，洞周围岩位移变化规律正常，位移量值较小，围岩稳定性较好。

(2)在开挖过程中，主要在洞室周边出现了拉应力或低压应力及较大的压应力区，在结构转折处出现了应力集中。经过弹塑性有限元计算，部分区域围岩出现拉裂屈服其应力场进行调整后在中控室的顶拱、底板、主副厂房的底板出现最大为0.43 MPa的拉应力区;前期开挖对洞室顶拱围岩的应力变形影响比较大，后期开挖随着开挖体的远离顶拱对顶拱围岩的应力变形基本上没有影响。锚杆最大拉应力为45 MPa，具有较高的安全性。

(3)围岩塑性区开始主要出现在洞室周边，随着开挖断面的扩大，塑性区向围岩深部发展，面积不断增大，开挖完成后塑性区面积达到最大。在整个开挖过程中，洞室顶拱围岩没有发生塑性破坏。

(4)通过计算分析可知整个开挖过程中，洞周围岩位移变化规律正常，量值较小，塑性区主要分布在洞室周边，围岩稳定性较好。但在洞室交叉口处围岩的变形较大，出现较大范围的塑性区，为此建议在开挖施工过程中及时对洞室交叉处做好锁扣衬砌并增加锚杆数量及锚固深度，以防止围岩局部失稳破坏。

［1］朱维申，何满潮.复杂条件下围岩稳定性与岩体动态施工力学［M］.北京:科学出版社，1996.(ZHU Weishen，HE Man-chao.Stability of Surrounding Rock in Complex Conditions and the Mechanics of Dynamic Construction of Rock Masses［M］.Beijing:Science Press，1996.(in Chinese))

［2］肖 明.地下洞室施工开挖三维动态过程数值模拟分析［J］.岩土工程学报，2000，22(4):421－425.(XIAO Ming.Three-Dimensional Numerical Model of Construction Process for Underground Opening［J］.Chinese Journal of Geotechnical Engineering，2000，22(4):421 －425.(In Chinese))

［3］陈宗基.发刊词［J］.岩石力学与工程学报，1982，1(1):Ⅲ － Ⅳ.(CHEN Zong-ji.Foreword to a Periodical［J］.Chinese Journal of Rock Mechanics and Engineering，1982，1(1):Ⅲ － Ⅳ.(in Chinese))

［4］陈宗基.地下巷道长期稳定性的力学问题［J］.岩石力学与工程学报，1982，1(3):1 － 20.(CHEN Zong-ji.The Mechanical Problems of Long-term Stability of Underground Galleries［J］.Chinese Journal of Rock Mechanics and Engineering，1982，1(3):1 －20.(in Chinese))

［5］郝跃天，杨更社，任建喜.J.M.Dancan反转应力法的探讨［J］.力学与实践，1994，16(2):32 －34.(HAO Yuetian，YANG Geng-she，REN Jian-xi.The Study of J.M.Dancan Reverse Stress Method［J］.Mechanics and Practice，1994，16(2):32 －34.(in Chinese))

［6］徐干成，白洪才，郑颖人，等.地下工程支护结构［M］.北京:中国水利水电出版社，2002.(XU Gan-cheng，BAI Hong-cai， ZHENG Ying-ren， et al.Supporting Structure of Underground Engineering［M］.Beijing:China Water Power Press，2002.(in Chinese))

［7］王勖成，绍 敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1997.(WANG Xucheng，SHAO Min.The Basic Principle and Numerical Methods of Finite Element Method［M］.Beijing:Tsinghua University Press，1997.(in Chinese))

［8］谷兆棋，彭守拙，李仲奎.地下洞室工程［M］.北京:清华大学出版社，1994.(GU Zhao-qi，PENG Shou-zhuo，LI Zhong-kui.Underground Excavation Engineering［M］.Beijing:Tsinghua University Press，1994.(in Chinese))

［9］王 镭.有限单元法中的隐式杆单元［J］.水利学报，1987，(8):59 － 62.(WANG Lei.Implicit Stem Cell of Finite Element Method［J］.Journal of Hydraulic Engineering，1987，(8):59 －62.(in Chinese))

［10］肖 明.地下洞室隐式锚杆柱单元的三维弹塑性有限元分析［J］.岩土工程学报，1992，14(5):19－26.(XIAO Ming.3-D Elastoplastic FEM Analysis of Implicit Cylindric Anchor Bar Element for Underground Opening［J］.Chinese Journal of Geotechnical Engineering，1992，14(5):19 －26.(in Chinese))

［11］杨述仁，周文铎.地下水电站厂房设计［M］.北京:中国水利电力出版社，1993.(YANG Shu-ren，ZHOU Wen-duo.Design of Underground Hydropower Station［M］.Beijing:China Water Resources and Electric Power Press，1993.(in Chinese))