基于综合结构势的结构性黄土双硬化参数模型

罗爱忠，邵生俊，陈昌禄，张 喆

(1.毕节学院建筑工程学院，贵州 毕节 551700;2.西安理工大学 岩土工程研究所，西安 710048)

1 研究背景

天然沉积的黄土具有较强的结构性，结构性与土的粒度、密度、湿度一样，是反映黄土物理力学性质的重要指标。从广义上讲，土都具有结构性［1］;从微观上讲，土的结构性是指土体颗粒、孔隙的性状和排列方式及颗粒之间的相互作用［2］。谢定义教授［3］基于原生结构破坏和次生结构生成过程的相互作用机理，从结构可稳性和结构可变性2个方面定义了土的综合结构势。国外学者［4－11］主要针对于软土的结构性及其本构关系展开了一定的研究。国内的研究相对于国外起步较晚，但近几年呈现蓬勃发展的势头，从沈珠江［12］开始，许多学者［13－17］针对于软土、黄土等特殊土展开了一系列的研究。但是，现有的非线性本构模型或弹塑性模型大部分只能对非结构性土的变形变化过程进行描述;或者针对结构性土的特性，对现有模型做出修正，没有考虑增湿和加荷引起的结构损伤演化规律，也就难以真实地反映结构性土的力学性状与应力应变的变化规律。沈珠江［18］在对剑桥模型及系列修正模型的基础上，提出了黏土的双硬化模型，该模型可以模拟正常固结黏土和一般超固结黏土。本文在黏土双硬化模型研究的基础上，引入表征黄土结构性的综合结构势，建立非饱和黄土结构性的增湿本构模型，由于不仅同时考虑了含水量和荷载这2个对湿陷性黄土力学特性有重要影响的因素，而且考虑了土体结构性随含水量和荷载的变化规律，因此，在非饱和黄土含水量场时空分布规律研究的基础上，它可以反映结构性黄土在含水率和应力连续变化条件下的变形和强度特性，使土的结构性研究和土体本构模型研究实现了有机的统一，开辟了湿陷性黄土结构性理论研究和实际应用的新途径。

2 综合结构势及强度参数变化规律

土的结构性理论认为黄土的骨架结构中，大孔隙孔壁的颗粒多为碳酸钙胶结呈筒壁状，结构稳定;架空孔隙是由骨架颗粒堆积所形成的，孔径远比构成孔隙的颗粒大;颗粒在平面上排列成犬牙交错形成粒间孔隙。黄土的排列和联接使其具有比较稳定的原生结构，在力学特性上表现出较高的初始结构强度。受到外荷载的作用时，如果外荷的大小不超过土的初始结构强度，土的原生结构不会发生破坏，颗粒间的相对位置不会发生位移或仅有较小的弹性变形。一旦主动应力超过了土的初始结构强度，将首先在部分颗粒的联结中出现微隙，进而出现颗粒的滑移。主动应力的继续增大，将进一步使这种微隙和滑移继续增大、增多，甚至出现颗粒团粒的破损和碎裂，并在更大的局部范围内发展，直至初始结构强度遭到完全的破坏。与此同时，颗粒间的相互移动和压密也形成新的次生结构。在这个原生结构破坏、次生结构形成的过程中，如果前者的影响远远超过后者的影响，则土将走向衰化或软化，直至最终的破坏，沿着某一个破裂面发生滑动;如果后者的影响大于前者的影响，则土将走向进一步的压实或硬化;如果前者和后者的影响的优势交错出现，则土将出现更为复杂的位移变化。谢定义［3，19］在考察土结构性研究历史的基础上，提出了一个表征土结构性及变化的定量化参数－综合结构势，该参数的最大优势在于它能够描述在外界条件变化时土结构性的变化规律，基于综合结构势，能够得到土体在外界环境变化条件后所表现出的土体结构性变化的真实响应。之后，许多学者将该思想继承和发展，提出了多种结构性参数［20－24］。在这些结构性参数中比较有影响的是应力比结构性参数mη，该参数定义为

式中:mη为应力比结构性参数;p为球应力;q为广义剪应力;下标i，r，s分别表示原状土、重塑土和饱和土，η为应力比。该式定义的结构性参数mη不仅考虑了剪应力对土结构性的作用，同时也反映了球应力对结构性的影响，是对应力结构性参数的继承和发展。

基于文献［20］的常规三轴试验应力应变曲线和式(1)，考察剪切过程中的应力比变化与变形发展的关系，整理得到应力比结构性参数的变化规律如图 1 所示［24］。

综合常规三轴条件下原状黄土结构性的变化规律，可以归纳出如下基本公式:

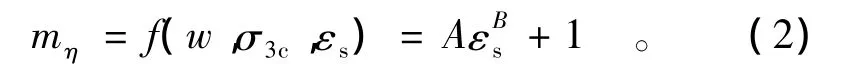
式中:A，B为与含水量和固结压力相关的参数;w为含水量;σ3c为固结围压;εs为塑性剪应变。通过数据分析可知，固结压力小于土的结构强度时，在相同含水量条件下，土的结构性参数与固结围压呈指数形式的变化规律;在相同的固结围压条件下，土的结构性参数与含水量呈线性变化规律。根据这一规律，结合数据分析，可以得出式(2)中的A，B值。

式(3)和式(4)中e为孔隙比，各参数按下面式计算:

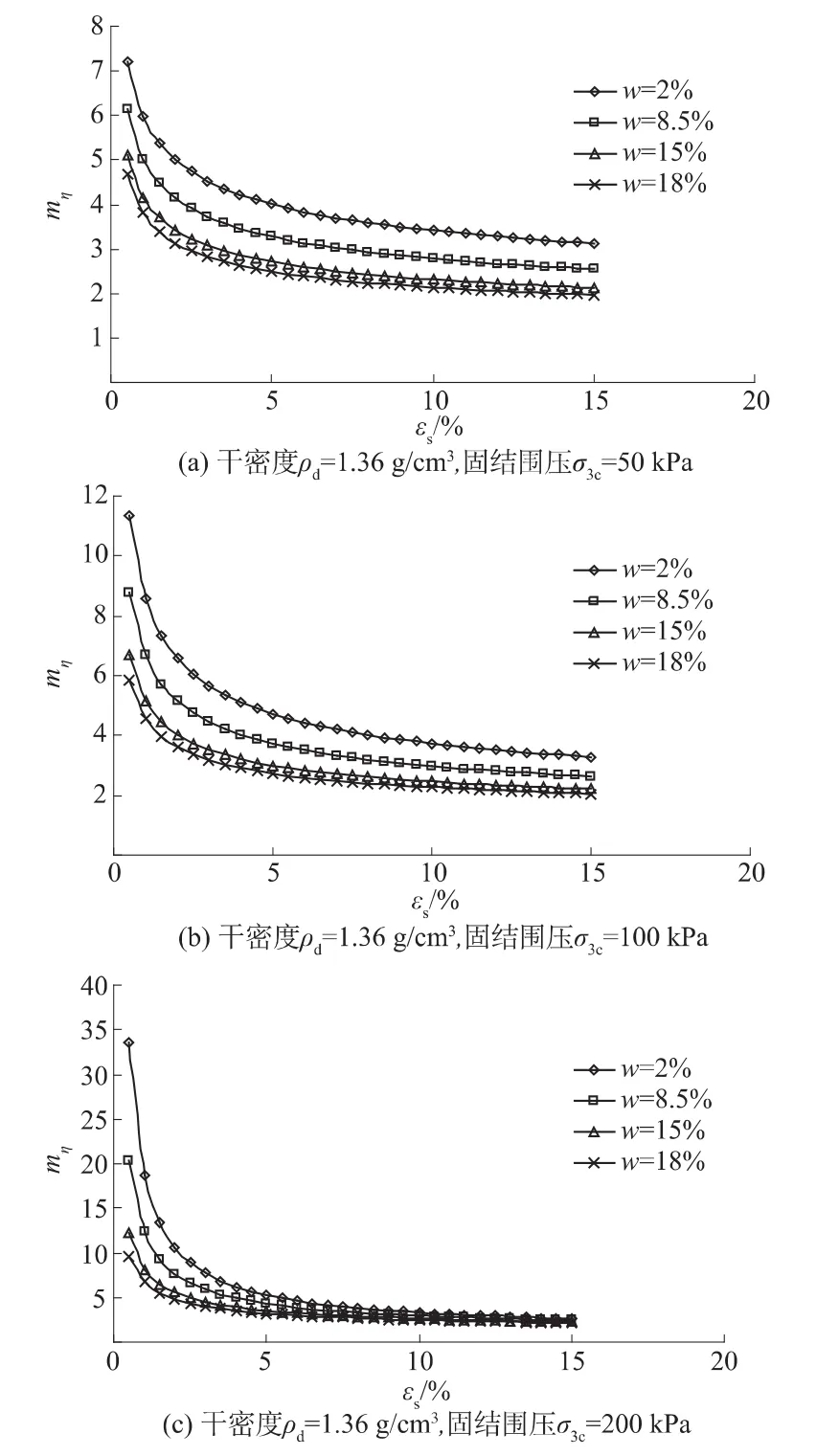
图1 土结构性参数随含水量的变化规律Fig.1 Regularity of the variation of structural index with water content

从式(2)建立的结构性参数可以看出，该结构性参数实际上反映了土体含水率、固结围压以及剪切变形之间的综合影响。随着含水量和剪切变形的增加，土的结构性逐渐减弱，最终稳定值为1，根据综合结构势思想，此时土体的结构性完全散失，土体趋于破坏。进一步整理结构性参数与黏聚力c、内摩擦角φ与结构性参数mη之间的关系，得到图2和图3。黏聚力与综合结构势参数之间符合指数函数关系，而内摩擦角对结构性参数基本变化不大。由此可见，随着土结构性的逐渐破坏，颗粒间的胶结作用逐渐减弱，黏聚力减低，当土的结构性遭到彻底破坏时，黏聚力趋近于0;此时无结构性的黄土与饱和正常固结黏土和砂土的力学性质类似。黏聚力与结构性参数的关系表达为

图2 黏聚力与综合结构势的关系Fig.2 The relationship between cohesion and structural potential

图3 内摩擦角与综合结构势的关系Fig.3 The relationship between internal friction angle and structural potential

式中:A1=288.042;A2=0.898 74。

为了考察式(2)至式(5)回归拟合参数的完备性，下面用拟合参数来预测结构性参数的变化规律及黏聚力的变化规律。由于篇幅有限，仅仅给出固结围压为100 kPa时的结构性参数预测曲线。从图4的拟合曲线可以看出，本文的拟合回归参数得到的结构性参数变化曲线与文献［24］中实测基本一致。

图4 结构性参数变化规律拟合曲线(100 kPa)Fig.4 Fitted curves of the variation regularity of structural index(100 kPa)

3 考虑结构性的黄土本构关系

3.1 黄土结构性变化的认识

土的结构性与土的密度、湿度一样，是天然土体的一种基本特性，而土的本构模型是在试验研究的基础上对土变形和强度特性的数学描述，它应该尽量反映影响土力学特性的主要因素。由于土是一种散粒体材料，在加载过程中不仅具有剪切塑性变形，而且具有显著的体积塑性变形。天然土在沉积形成过程中一般均具有结构性，沉积时间越长，土骨架越稳定、联结作用越强，土的结构性越强。按照综合结构势的认识，正常固结土就处于重塑、饱和状态，因此，其结构性参数始终等于1。也就是说，正常固结土剪切过程的结构性恒定不变。与正常固结土比较，结构性土弹塑性本构模型建立时需考虑结构性对土加载过程中压缩变形和塑性变形特性的影响。另外，对于由于应力所导致的无结构性的超固结土，在剪切过程的结构性也应该是恒定不变的。基于上面的思考，通过压缩试验确定与结构性相关的准先期固结压力和e-lnp压缩曲线直线段斜率，它可以确定屈服面的大小与结构性之间的关系以及结构性土的压缩特性(见图5);基于对土结构性与强度之间的关系研究，得到结构性变化过程中临界状态线的变化规律(见图6);根据结构性参数归一化后的应力应变关系曲线呈双曲线变化的性质，认为同一结构性参数条件下土仍然服从临界状态土力学理论，将同一结构性参数条件下的压缩特性和临界状态线引入无结构性土的模型。

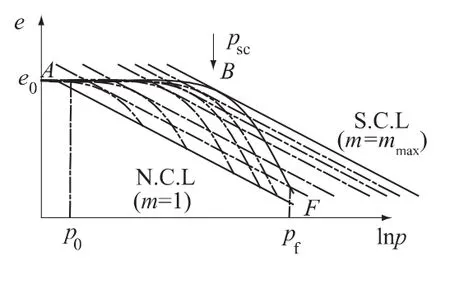
图5 结构性土的压缩曲线Fig.5 Compression curves of structural loess under different moistures

图6 结构性土的剪切屈服面Fig.6 Shear yield surface of structural loess under different moistures

3.2 考虑结构性的双硬化模型

沈珠江［18］提出的黏土的双硬化参数模型建议了一个包含塑性体应变和偏应变2个硬化参数的封闭屈服面模型。模型沿用了剑桥模型的参数测定方法。由于该模型的屈服面除了随硬化参数的积累而扩大和缩小外，还会因为2个参数比例不同而产生变形。因此，双硬化模型对于无结构性的正常固结土和超固结土具有很好的适应能力。本文对该模型做了一定的修正，通过屈服面和临界状态面的平移变化反应结构性的影响，如图7所示。

此时的屈服函数可以表示为

硬化规律如式(9)和式(10):

式中:p0为时的参考应力为塑性体积应为重塑饱和黄土的内摩擦角;n=1.2;ca，α 为材料参数。

3.3 结构性双硬化模型的应力应变关系

根据一致性原则，由式(6)有变;压缩指数 cc=λ(1+e0);cs=κ(1+e0);λ，κ为e-lnp压缩曲线与回弹曲线斜率;e0为初始孔隙比;

图7 考虑结构性的双硬化模型屈服面Fig.7 Double hardening yield surfaces in consideration of structural behavior

由相关联流动法则有

将式(12)代入式(11)得

式中:

将式(13)代入式(12)得

其中A为硬化模量，

弹性应变可由下列体积模量计算得

式中:pm为最大固结压力。黄土的泊松比假定为ν =0.30。

4 模型验证

对于黏土双硬化模型，文献［18］已经验证了模型在各种应力路径条件下的实用性。本文主要是在该模型的基础上考虑了黄土的结构性影响。因此应对于上述方程中的各分项，与一般双硬化模型的不同点主要是对黏聚力和结构性参数的偏导。通过对本文试验数据的分析得到模型的计算参数见表1。与结构性参数相关的参数对于不同固结围压和不同的初始含水量可以通过式(3)和式(4)计算得到。由于篇幅有限，本文只进行了固结围压为100 kPa、初始含水率为2%和固结围压为100 kPa、初始含水率为15%2种情况下的实测数据和模型预测数据对比。图8给出了这2种情况下的试验结果与模型预测结果对比情况。从图8中可见，模型预测结果与实测试验结果基本吻合。对于体变出现剪胀的情况得到了很好的模拟，但对体变剪缩的情况，模型预测结果偏硬，在变形发展后期，模型预测结果相对于实测结果出现了一定偏差，模型预测结果相对大于实测结果;对于剪应力应变关系，2种情况都得到了很好的模拟，模型预测结果和实测结果吻合较好。

表1 计算参数Table 1 Calculation parameters

图8 应力应变关系对比曲线Fig.8 Comparion of stress-strain curves

总的说来，在双硬化模型的基础上通过综合结构势的思想考虑了黄土结构性，进一步将黄土对水的敏感性考虑进土体本构关系中，使得结构性黄土试样的宏观应力应变特性得到合理描述。

5 结语

(1)基于综合结构势的思路，提出了综合结构势的定量化参数，该参数与广义剪应变之间存在幂函数关系。

(2)考虑结构参数与强度参数之间的关系，得到了两者的具体数学描述。

(3)在黏土双硬化模型的基础上引入结构性参数的影响，建立了考虑黄土结构性的双硬化模型。

(4)通过模型预测与实测结果的对比分析，验证了考虑黄土结构性的双硬化模型的合理性，该模型能很好地预测黄土的宏观应力应变特性。

［1］龚晓南，熊传祥，项可祥，等.粘土结构对其力学性质的影响及形成原因分析［J］.水利学报，2000，(10):43－47.(GONG Xiao-nan，XIONG Chuan-xiang，XIANG Kexiang，et al.The Formation of Clay Structure and Its Influence on Mechanical Characteristics of Clay［J］.Journal of Hydraulic Engineering，2000，(10):43 － 47.(in Chinese))

［2］胡瑞林.粘性土微结构定量模型及其它工程地质特征研究［M］.北京:北京地质出版社，1995.(HU Rui-lin.Research on Quantitative Microstructure Models of Natural Clayed Soils and Its Engineering Geology Characteristics［M］.Beijing:Beijing Geological Publishing House，1995.(in Chinese))

［3］谢定义，姚仰平，党发宁.高等土力学［M］.北京:高等教育出版社，2008.(XIE Ding-yi，YAO Yang-ping，DANG Fa-ning.Advanced Soil Mechanics［M］.Beijing:Higher Education Press，2008.(in Chinese))

［4］BAUDET B，STALLEBRASS S.A Constitutive Model for Structured Clays［J］.Geotechnique，2004，54(4):269 －278.

［5］BURLAND J B.30th Rankine Lecture:On the Compressibility and Shear Strength of Natural Clays［J］.Geotechnique，1990，40(3):327－378.

［6］KAVVADAS M，AMOROSI A.A Constitutive Model for Structured Soils［J］.Geotechnique，2000，50(3):263 －274.

［7］LEROUEIL S，TAVENAS F，BRUCY F，et al.Behaviour of Destructured Natural Clays［J］.Journal of Geotechnical Engineering，ASCE，1979，105(6):759－778.

［8］ROUAINIA M，WOOD D M.A Kinematic Hardening Constitutive Model for Natural Clays with Loss of Structure［J］.Geotechnique，2000，50(2):153 －164.

［9］LIU M D，CARTER J P.Virgin Compression of Structured Soils［J］.Geotechnique，1999，49(1):43 －57.

［10］LIU M D，CARTER J P.Modelling the Destructuring of Soils During Virgin Compression［J］.Geotechnique，2000，50(4):479－483.

［11］SUEBSUK J，HORPIBULSUK S，LIU M D.Modified Structured Cam Clay:A Generalized Critical State Model for Destructured，Naturally Structured and Artificially Structured Clays［J］.Computers and Geotechnics，2010，37(7/8):956－968.

［12］沈珠江.结构性粘土的弹塑性损伤力学模型［J］.岩土工程学报，1993，15(3):21 －28.(SHEN Zhu-jiang.An Elasto-Plastic Damage Model for Cemented Clays［J］.Chinese Journal of Geotechnical Engineering，1993，15(3):21 －28.(in Chinese))

［13］刘恩龙，沈珠江.结构性土压缩曲线的数学模拟［J］.岩土力学，2006，27(4):615 － 620.(LIU En-long，SHEN Zhu-jiang.Modeling Compression of Structured Soils［J］.Rock and Soil Mechanics，2006，27(4):615 －620.(in Chinese))

［14］何开胜，沈珠江.结构性粘土的弹黏塑性损伤本构模型［J］.水利水运工程学报，2002，(4):7 －13.(HE Kai-sheng，SHEN Zhu-jiang.Elasto-Viscoplastic Damage Model for Structural Clays［J］.Hydro-science and Engineering，2002，(4):7 －13.(in Chinese))

［15］罗晓辉，白世伟.结构性土体强度的统计损伤模型分析［J］.岩土工程学报，2004，26(5):712 －714.(LUO Xiao-hui，BAI Shi-wei.Model Analysis on Statistical Damage of Strength of Cemented Soil［J］.Chinese Journal of Geotechnical Engineering，2004，26(5):712 － 714.(in Chinese))

［16］金 旭，赵成刚，刘 艳，等.非饱和原状黄土的弹塑性损伤本构模型［J］.北京交通大学学报，2010，34(1):78 －82.(JIN Xu，ZHAO Cheng-gang，LIU Yan，et al.An Elasto-Plastic Damage Constitutive Model of Unsaturated Soils［J］.Journal of Beijing Jiaotong University，2010，34(1):78 －82.(in Chinese))

［17］胡再强，沈珠江，谢定义.结构性黄土的本构模型［J］.岩石力学与工程学报，2005，24(4):17－21.(HU Zaiqiang，SHEN Zhu-jiang，XIE Ding-yi.Constitutive Model of Structural Loess［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(4):17 － 21.(in Chinese))

［18］沈珠江.粘土的双硬化模型［J］.岩土力学，1995，16(1):1 －8.(SHEN Zhu-jiang.A Double Hardening Model for Clays［J］.Rock and Soil Mechanics，1995，16(1):1 －8.(in Chinese))

［19］谢定义，齐吉琳.土结构性及其定量化参数研究的新途径［J］.岩土工程学报，1999，21(6):651－656.(XIE Ding-yi，QI Ji-lin.Soil Structure Characteristics and New Approach in Research on Its Quantitative Parameter［J］.Chinese Journal of Geotechnical Engineering，1999，21(6):651 －656.(in Chinese))

［20］邵生俊，周飞飞，龙吉勇.原状黄土结构性及其定量化参数研究［J］.岩土工程学报，2004，26(4):531 －536.(SHAO Sheng-jun，ZHOU Fei-fei，LONG Ji-yong.Structural Properties of Loess and Its Quantitative Parameter［J］.Chinese Journal of Geotechnical Engineering，2004，26(4):531 －536.(in Chinese))

［21］陈存礼，胡再强，高鹏.原状黄土的结构性及其与变形特性关系研究［J］.岩土力学，2006，27(11):1891－1896.(CHEN Cun-li，HU Zai-qiang，GAO Peng.Research on Relationship Between Structure and Deformation Property of Intact Loess［J］.Rock and Soil Mechanics，2006，27(11):1891 －1896.(in Chinese))

［22］冯志炎.非饱和黄土结构性定量化参数与结构性本构关系研究［D］.西安:西安理工大学，2008.(FENG Zhiyan.Structural Quantitative Parameter and Structural Constitutive Relationship of Unsaturated Loess［D］.Xi’an:Xi’an University of Technology，2008.(in Chinese))

［23］骆亚生，谢定义.复杂应力条件下土的结构性本构关系［J］.四川大学学报(工程科学版)，2005，37(5):14 －18.(LUO Ya-sheng，XIE Ding-yi.Structural Constitutive Relation of Soils Under Complex Stress Conditions［J］.Journal of Sichuan University(Engineering Science Edition)，2005，37(5):14－18.(in Chinese))

［24］邓国华.真三轴条件下结构性土的强度变形本构关系研究［D］.西安:西安理工大学，2009.(DENG Guohua.Research on Strength and Deformation Constitutive Relations of Structured Soils under True Triaxial Condition［D］.Xi’an:Xi’an University of Technology，2009.(in Chinese ))