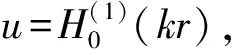解声波散射问题的一种优化PML方法
杨孝英, 王旖旎
(长春工业大学 基础科学学院, 长春 130012)
自从Bérenger[1]提出解电磁散射问题的PML方法以来, 已构造了许多不同的PML方法[2-4]. 文献[5-6]用PML方法求解了洞穴散射问题, 但在实际计算中, 若PML的厚度过大, 则用有限元计算需要大量的剖分节点, 从而导致数值计算耗费内存和计算时间. 因此PML参量的确定是实际计算的关键. 本文提出一种带小参数的PML, 并证明了如此构造的PML吸收效果较好.
1 解散射问题的优化PML方法
考虑散射问题:
(1)

a(u,ψ)=(g,ψ)ΓD, ∀ψ∈H1(ΩR),
(2)
其中: (·,·)表示L2内积;
(3)
算子T:H1/2(ΓR) →H-1/2(ΓR)定义为
∀f∈H1/2(ΓR).
(4)
则问题(2)的解存在唯一[8].
针对上述问题, Chen等[7]给出了圆形PML区域的自适应有限元方法; Bermúdez等[9]针对方形PML区域给出了解散射问题的一种优化PML方法, 即选取PML介质参量为在PML广义积分无界的函数, 这样选取的参量能保证PML计算与PML的厚度无关, 从而节省了计算量. 但文献[9]选取的介质参量函数使PML方程的系数产生奇异, 因此导致数值分析及截断PML问题的收敛性分析存在困难, 并且在数值计算中, 边界层附近的PML解出现不稳定现象.
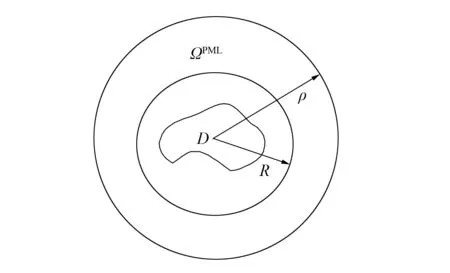
图1 优化PML的几何构造Fig.1 Geometric structure of optimal PML
本文基于文献[7,9], 针对圆形PML区域提出一种新的PML介质参量构造方法. 如图1所示, 在区域ΩPML={x∈R2:R (5) 其中:ε0为足够小的正数;m≥2. 令 (6) (7) (8) 证明: 由式(8), 有 由于 故 其中δ为PML的厚度. 证毕. (9) 例2考虑金属凹槽的散射问题. 入射平面波为ui=eikx, 在其边界上散射场u=-ui. 图3为δ=1,2,0.5,ε0=0.01,0.005,0.001时PML解的实部曲线. 由图3可见, 优化的PML方法对于解金属凹槽散射问题有效. [1] Bérenger J P. Perfectly Matched Layer (PML) for Computational Electromagnetics [M]. [S.l.]: Morgan & Claypool Publishers, 2007. [2] CHEN Zhi-ming. Convergenc of the Time-Domain Perfectly Matched Layer Method for Acoustic Scattering Problems [J]. Inter J Numer Anal Mode, 2009, 6(1): 124-146. [3] LIU Juan, MA Fu-ming. A PML Method for Electromagnetic Scattering from Two-Dimensional Overfilled Cavities [J]. Communications in Mathematical Research, 2009, 25(1): 51-66. [4] YANG Xiao-ying, MA Fu-ming, DU Xin-wei. A Uniaxial Optimal Perfectly Matched Layer Method for Time-Harmonic Scattering Problems [J]. Communications in Mathematical Research, 2010, 26(3): 255-268. [5] ZHANG De-yue, MA Fu-ming, FANG Ming. Finite Element Method with Perfectly Matched Absorbing Layers for Wave Scattering from a Cavity [J]. Chinese Journal of Computational Physics, 2008, 25(3): 301-308. [6] YANG Xiao-ying, MA Fu-ming, DU Xin-wei. An Optimal PML Method for Electromagnetic Scattering from Cavities [J]. Journal of Jilin University: Science Edition, 2009, 47(2): 185-190. (杨孝英, 马富明, 杜新伟. 计算开洞穴电磁散射问题的一种优化PML方法 [J]. 吉林大学学报: 理学版, 2009, 47(2): 185-190.) [7] CHEN Zhi-ming, LIU Xue-zhe. An Adaptive Perfectly Matched Layer Technique for Time-Harmonic Scattering Problems [J]. SIAM J Numer Anal, 2005, 43(2): 645-671. [8] Colton D L, Kress R. Integral Equation Methods in Scattering Theory [M]. New York: John Wiley and Sons, 1983. [9] Bermúdez A, Hervella-Nieto L, Prieto A, et al. An Optimal Perfectly Matched Layer with Unbound Absorbing Function for Time-Harmonic Acoustic Scattering Problems [J]. J Comput Phys, 2007, 223(2): 469-488.
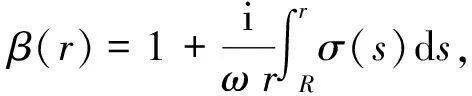
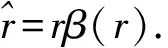
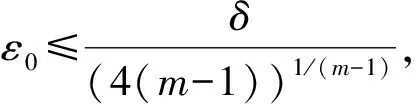

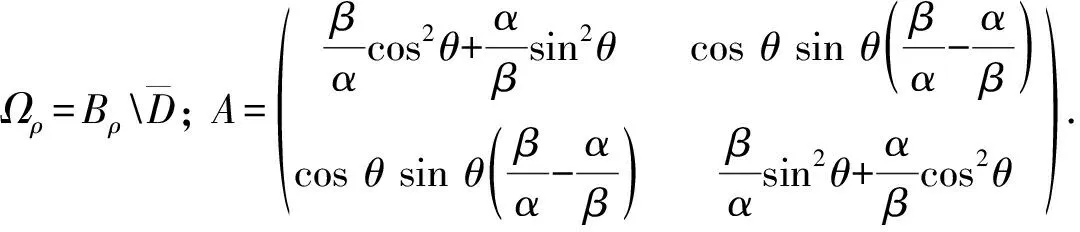
2 数值实例