(行列)反对称矩阵的极分解及其广义逆
袁 晖 坪
(重庆工商大学 电子商务及供应链系统重庆市重点实验室, 数学与统计学院, 重庆 400067)
0 引 言

定义1设A=(aij)∈Cm×n, 则称
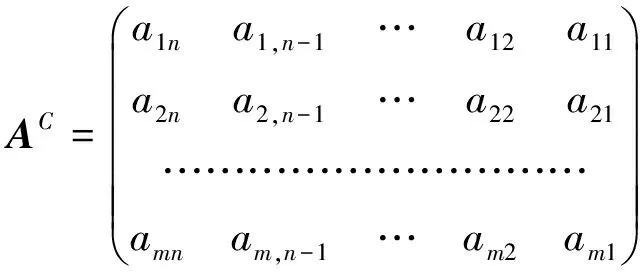
分别为矩阵A的行转置矩阵与列转置矩阵, 并记为AR和AC. 特别地, 若AR=A(AC=A), 则称A为行(列)对称矩阵; 若AR=-A(AC=-A), 则称A为行(列)反对称矩阵.

1 行(列)反对称矩阵的极分解及广义逆
引理1[15]设A∈Cm×n, 则对任何酉矩阵U∈Cm×m,V∈Cn×n有UAV的Moore-Penrose逆:
(UAV)+=VHA+UH.
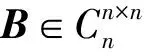
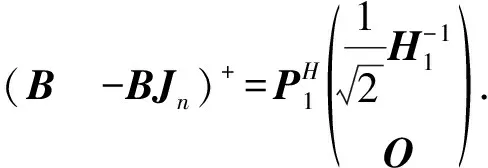
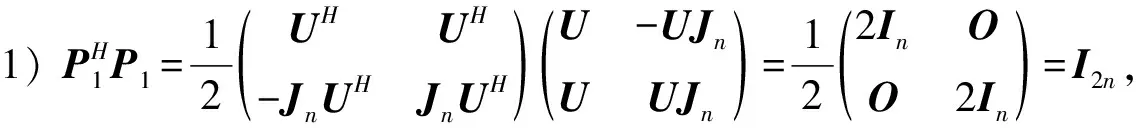

2) 由1)、 引理1及文献[15], 有
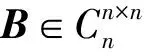

证明:
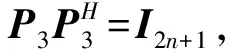

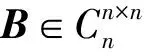
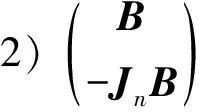
定理3的证明与定理1的证明类似, 故略.
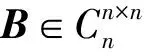

定理4的证明与定理2的证明类似, 故略.
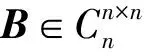
证明: 1) 与定理1和定理3的证明类似, 故略. 2) 与定理2和定理4的证明类似, 故略.
2 行(列)反对称矩阵极因子的扰动界
引理2设a1,a2,…,an,b1,b2,…,bn均为复数, 则
证明: 由复数的性质及Cauchy-Schwarz不等式, 有
引理3设A∈Cm×n,Bij∈Cn×s,i,j=1,2,…,k, 则
证明: 由矩阵Frobenius范数的定义和引理2可知结论成立.


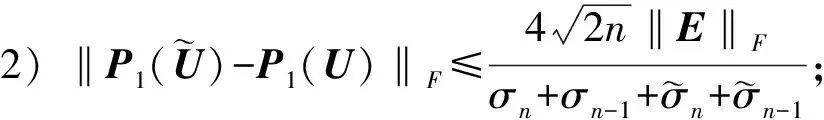
证明: 由定理1知1)成立; 由引理3和引理4知
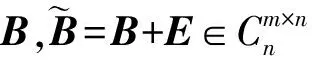
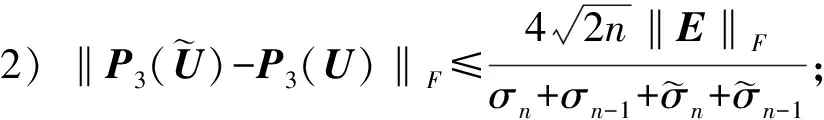
证明: 由定理2知1)成立; 由引理3和引理4知:
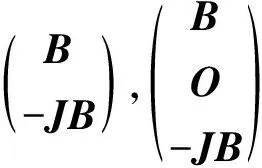
综上所述, 本文研究了行(列)反对称矩阵的极分解、 广义逆和扰动界, 得出了行(列)反对称矩阵与母矩阵两者的极分解、 广义逆和扰动界之间的定量关系. 结果表明, 用母矩阵代替行(列)反对称矩阵计算极分解、 广义逆和扰动界, 既减少了计算量和储存量, 又保证了数值精度.
[1] SUN Ji-guang, CHEN Chun-hui. Generalized Polar Decomposition [J]. Math Numer Sinica, 1989, 11(3): 262-273.
[2] CHEN Xiao-shan, LI Wen, SUN Wei-wei. Some New Perturbation Bounds for the Generalized Polar Decomposition [J]. BIT Numerical Mathematics, 2004, 44(2): 237-244.
[3] LI Wen, SUN Wei-wei. New Perturbation Bounds for Unitary Polar Factors [J]. SIAM J Matrix Anal and Appl, 2003, 25(2): 362-372.
[4] Chaitin-chatelin F, Gratton S. On the Condition Numbers Associated with the Polar Factorization of a Matrix [J]. Numer Linear Algebra with Appl, 2000, 7(5): 337-354.
[5] LI Wen, SUN Wei-wei. Perturbation Bounds of Unitary and Subunitary Polar Factors [J]. SIAM J Matrix Anal and Appl, 2002, 23(4): 1183-1193.
[6] YANG Hu, LI Han-yu. Perturbation Bounds for Weighted Polar Decomposition in the Weighted Unitarily Invariant Norm [J]. Numer Linear Algebra with Appl, 2008, 15(8): 685-700.
[7] YANG Hu, LI Han-yu. Weighted Polar Decomposition [J]. J Math Res Exposition, 2009, 29(5): 787-798.
[8] YANG Hu, LI Han-yu. Weighted Polar Decomposition and WGL Partial Ordering of Rectangular Complex Matrices [J]. SIAM J on Matrix Anal and Appl, 2008, 30(2): 898-924.
[9] LI Ren-cang. Relative Perturbation Bounds for Positive Polar Factors of Graded Matrices [J]. SIAM J Matrix Anal and Appl, 2006, 27(2): 424-433.
[10] LI Wen, SUN Wei-wei. Combinatorial Perturbation Bound: Ⅱ.Polar Factorization [J]. Science of China Series A: Mathematics, 2007, 37(6): 701-708. (黎稳, 孙伟伟. 组合扰动界: Ⅱ.极分解 [J]. 中国科学A辑: 数学, 2007, 37(6): 701-708.)
[11] WANG Wei-guo, LIU Xin-guo. Several New Results on the Polar Decomposition and Generalized Polar Decomposition [J]. Mathematica Numerica Sinica, 2008, 30(2): 147-156. (王卫国, 刘新国. 关于极分解和广义极分解的一些新结果 [J]. 计算数学, 2008, 30(2): 147-156.)
[12] LIU Yong-hui, TIAN Yong-ge. A Mixed-Type Reverse Order Law for Generalized Inverse of a Triple Matrix Product [J]. Acta Mathematica Sinica: Chinese Series, 2009, 52(1): 197-204. (刘永辉, 田永革. 矩阵广义逆的一个混合反序律 [J]. 数学学报: 中文版, 2009, 52(1): 197-204.)
[13] ZOU Hong-xing, WANG Dian-jun, DAI Qiong-hai, et al. QR Factorization for Row or Column Symmetric Matrix [J]. Science of China: Series A, 2002, 32(9): 842-849. (邹红星, 王殿军, 戴琼海, 等. 行(或列)对称矩阵的QR分解 [J]. 中国科学: A辑, 2002, 32(9): 842-849.)
[14] YUAN Hui-ping. Determinantal Inequality of Generalized Positive Subdefinite Matrices [J]. Journal of Jilin University: Science Edition, 2004, 42(3): 346-350. (袁晖坪. 广义次正定矩阵的行列式不等式 [J]. 吉林大学学报: 理学版, 2004, 42(3): 346-350.)
[15] 张贤达. 矩阵分析与应用 [M]. 北京: 清华大学出版社, 2004: 85-89.

