求解加权Euclidean单中心问题的SMO-型算法

丛 伟 杰

(西安邮电大学 理学院,西安 710121)

0 引 言

给定点集P={p1,p2,…,pm}⊂Rn和对应的正权重W=(w1,w2,…,wm}；加权Euclidean单中心(weighted Euclidean one-center,简记为WEOC)问题就是寻找一个点c∈Rn,最小化P中各点到c加权Euclidean距离的最大值. 给定(P,W)的WEOC问题记为WEOC(P,W),可表示为

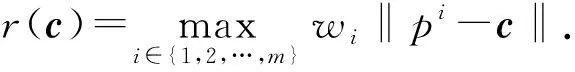
WEOC问题[1-3]是计算几何中的经典问题,在现代工程学和数学领域应用广泛,尤其在设施选址问题上[4-5]. 当WEOC问题中的所有权重wi=1时,WEOC问题即退化为最小闭包球(minimum enclosing ball,简记为MEB)问题[6],即寻找一个半径最小的球包含点集P中的所有点.

序列最小最优化(sequential minimal optimization,简记为SMO)方法[7]是支持向量机中求解凸二次优化问题的主要工具,与一般传统优化迭代方法不同,SMO方法在每次迭代过程中只需更新决策变量的两个分量,节省了计算时间,能加速算法的执行. 本文首先定义了求解WEOC问题的两个近似最优性条件,然后基于SMO方法的思想,提出一种求解WEOC问题的SMO-型算法. 该算法求解WEOC问题满足第二个近似最优性条件的(1+ε)-近似解. 数值实验结果验证了算法的有效性.

1 优化公式及近似最优性条件

WEOC(P,W)问题可以转化为如下优化问题:

(1)

其中c=(c1,c2,…,cn)T∈Rn和r∈R是原始变量. 文献[3]通过平方问题(1)的约束并定义γ=r2,将问题(1)转化为如下凸优化问题:

(2)

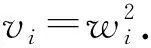
(3)

其中u=(u1,u2,…,um)T∈Rm是对偶变量. 由问题的KKT最优性条件[3]可得

(4)

其中(c*,r*)∈Rn×R和u*∈Rm分别为原规划(1)和对偶规划(3)的最优解. 因此,WEOC(P,W)问题能转化为求解对偶规划(3).

(5)

下面类似于MVAE问题的近似最优性条件[8],给出WEOC问题的两个近似最优性条件定义.

定义1给定ε>0,如果

wi‖pi-c‖≤(1+ε)r,i=1,2,…,m,

(6)

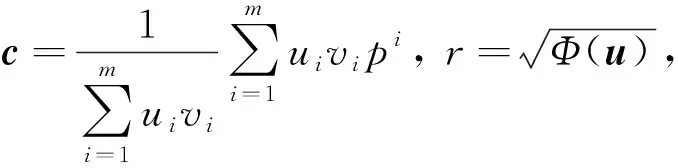
定义2给定ε∈(0,1),如果式(6)成立,并且有

ui>0 ⟹wi‖pi-c‖≥(1-ε)r,i=1,2,…,m,

(7)

则称对偶规划(3)的可行解u满足强ε-近似最优性条件.

由定义2可知,当ui>0时,有(1-ε)r≤wi‖pi-c‖≤(1+ε)r(i=1,2,…,m),表明对于充分小的ε,定义2是比定义1对式(5)更好的近似.

2 SMO-型算法

下面给出求解WEOC(P,W)问题的SMO-型算法.

算法1给定P={p1,p2,…,pm}⊂Rn,W={w1,w2,…,wm},ε>0.

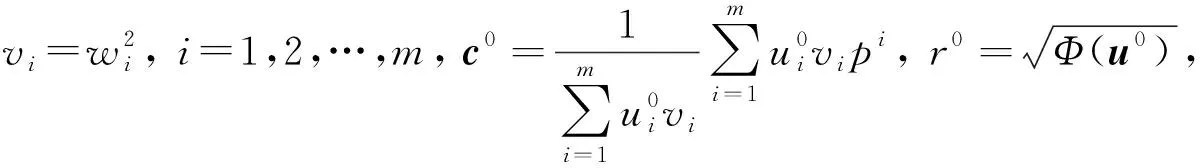
4) 令

算法1中1)是简单的初始化过程,与文献[3]中算法5.1的初始化过程相同. 算法1与算法5.1[3]的主要不同在于主循环部分,在第k次迭代中,由2)和3)可得

wi+‖pi+-ck‖=(1+ε+)rk≤(1+εk)rk,wi-‖pi--ck‖=(1-ε-)rk≥(1-εk)rk,

表明每次迭代算法1总能得到对偶规划(3)的一个可行解uk满足强εk-近似最优性条件. 因此,当算法终止(εk≤ε)时,得到的可行解uk满足强ε-近似最优性条件(6),(7),并且有

由WEOC(P,W)的(1+ε)-近似解定义知,算法1终止时,得到问题的一个(1+ε)-近似解为(ck,r(ck))∶=(ck,(1+εk)rk).

算法5.1[3]给出的可行解迭代更新公式为uk+1=(1-λk)uk+λkei+=uk+λk(ei+-uk)或uk+1=(1+λk)uk-λkei-=uk+λk(uk-ei-),其中ei表示第i个分量为1的单位向量. 它们使用了两个不同的搜索方向dk∶=ei+-uk或uk-ei-,导致算法5.1[3]计算非常复杂的步长λk. 基于SMO方法的思想,每次迭代仅更新可行解的两个分量,算法1中4)给出的可行解迭代更新公式为

uk+1=uk+λk(ei+-ei-),

(8)

其中搜索方向为dk∶=ei+-ei-,使得算法1能够计算一个相对简单的步长λk.

(9)

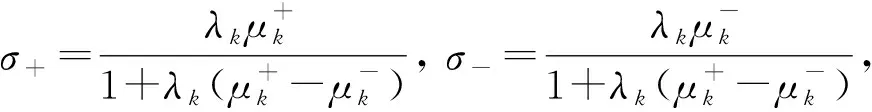
ck+1=(1-(σ+-σ-))ck+σ+pi+-σ-pi-.

(10)

对于任意的x,y,z∈Rm和σ1,σ2∈R ,易验证下式成立:

下面计算算法1中的步长λk. 由前面的计算可得Φ(uk+1)=Φ(uk)+Δk(λk),其中

(12)

对式(12)中关于λ的函数Δk(λ)分别求一、 二阶导数,得

3 数值实验

为了验证本文提出SMO-型算法的有效性,对于相同的数据集,在Matlab中同时执行文献[3]中的算法5.1和本文的算法1. 实验中用到的数据集是由函数randn(n,m)随机产生的正态分布数据,对应的权重是由函数rand(1,m)随机产生的均匀分布数据,其中(n,m)=(10,10 000)～(100,100 000). 对于每对固定的(n,m),随机产生10组不同的数据执行算法,得到的结果以其算术平均值形式给出.

表1列出了当精度ε=10-7时,两个算法执行的迭代次数和CPU时间的比较结果. 由表1可见: 算法1总比算法5.1[3]运行速度快,一般在迭代次数和CPU时间上比算法5.1减少41%～56%;对于n=100,m=100 000的大规模数据,算法1仅需要执行约90 s,表明算法1能有效求解高精度的大规模计算问题.

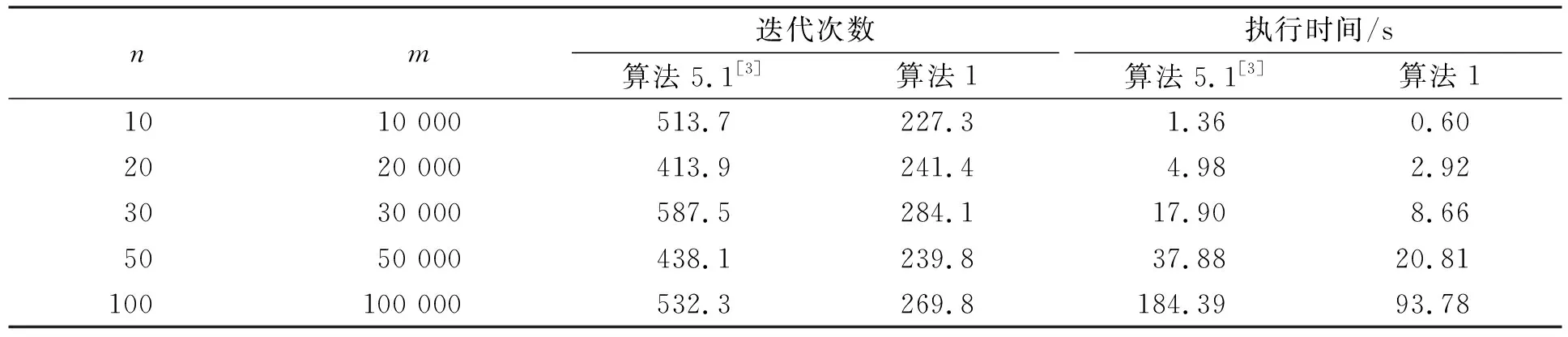
表1 算法5.1[3]和算法1在高精度ε=10-7下的数值结果比较Table 1 Comparisons of numerical results by virtue of algorithms 5.1[3] and 1 with ε=10-7

[1] Megiddo N. The Weighted Euclidean 1-Center Problem [J]. Mathematics of Operations Research,1983,8(4): 498-504.

[2] Megiddo N,Zemel E. AnO(nlogn) Randomizing Algorithm for the Weighted Euclidean 1-Center Problem [J]. Journal of Algorithms,1986,7(3): 358-368.

[3] Kumar P,Yildirim E A. An Algorithm and a Core Set Result for the Weighted Euclidean One-Center Problem [J]. Informs Journal on Computing,2009,21(4): 614-629.

[4] Drezner Z,Gavish B.ε-Approximations for Multidimensional Weighted Location Problems [J]. Operations Research,1985,33(4): 772-783.

[5] Drezner Z. The Weighted Minimax Location Problem with Set-up Costs and Extensions [J]. Operations Research,1991,25(1): 55-64.

[6] CONG Wei-jie,LIU Hong-wei. An SMO-Type Method for Solving the MEB Problem [J]. Journal of Northwest University: Natural Science Edition,2010,40(6): 965-969. (丛伟杰,刘红卫. 求解MEB问题的一种SMO-型方法 [J]. 西北大学学报: 自然科学版,2010,40(6): 965-969.)

[7] Chen P H,Fan R E,Lin C J. A Study on SMO-Type Decomposition Methods for Support Vector Machines [J]. IEEE Transactions on Neural Networks,2006,17(4): 893-908.

[8] CONG Wei-jie,LIU Hong-wei. Linearly Convergent Algorithm for Solving the Minimum Volume Axis-Aligned Ellipsoid Problem [J]. Journal of Jilin University: Science Edition,2011,49(2): 173-178. (丛伟杰,刘红卫. 求解最小体积轴向椭球问题的线性收敛算法 [J]. 吉林大学学报: 理学版,2011,49(2): 173-178.)