具有2n个解的绝对值方程问题

雍龙泉,刘三阳,拓守恒,熊文涛,史加荣

(1. 西安电子科技大学 应用数学系,西安 710071;2. 陕西理工学院 数学与计算机科学学院,陕西 汉中 723001;3. 湖北工程学院 数学与统计学院,湖北 孝感 432000;4. 西安建筑科技大学 理学院,西安 710055)

0 引言与预备知识

考虑问题:

Ax-|x|=b,

(1)

其中:A∈Rn×n;x,b∈Rn;|x|表示对x的各分量取绝对值. 问题(1)称为绝对值方程(absolute value equations,AVE),它是文献[1]提出的绝对值矩阵方程Ax+B|x|=b的重要子类.

关于AVE的研究主要源于两方面：一是区间线性方程[1-2];二是线性互补问题. 目前对于AVE的研究主要集中于理论[3-12]和算法[13-35]两方面,前者主要研究解的存在性和唯一性;后者主要建立有效的算法并分析算法的收敛性. 本文给出了AVE问题解存在的条件,构造了一些具有2n个解的AVE问题,并指出了求解多解绝对值方程应注意的问题.

考虑Ax-|x|=b,若令A=I,b=0,则任意的x≥0都是AVE问题的解,此时AVE问题具有无穷多个解.

定理1[3]对AVE问题,若存在r∈Rn满足r≥ATr≥-r,bTr>0,则AVE无解.

定理2[3]若0≠b≥0,且‖A‖<1,则AVE无解.

定理3[3]如果A的特征值不为1,并且A的奇异值大于或等于1,则当集合

{x|(A+I)x-b≥0,(A-I)x-b≥0}≠Ø

时,AVE问题的解存在.

定理4[3]若矩阵A的奇异值大于1,则对任意的b∈Rn,AVE存在唯一解.

推论1[3]对任意的b,如果‖A-1‖<1,则AVE存在唯一解.

定理5[3]如果A≥0,‖A‖<1,b≤0,则AVE存在非负解.

如果区间矩阵[A-I,A+I]正则,则对于任意的b∈Rn,AVE有唯一解[9-10]. 该条件弱于矩阵A的奇异值大于1. 事实上,该条件恰好是文献[7]的特例.

1 2n个解存在的条件

证明: 分两步.

1) 证明在满足上述条件下,方程Ax-x=b有唯一的正解x*.

构造迭代过程xk+1=Axk-b,由于‖A‖∞<γ/2≤0.5<1,从而对于任意给定的初始点x0,迭代产生的序列{xk}都收敛,假设收敛点为x*,则x*唯一.

不妨取x0=-b,由于xk+1=Axk-b,则

从而

于是

‖xk+1-xk‖∞<(γ/2)k+1‖b‖∞,k=0,1,2,…

又由于

结合x0=-b,则有

2) 证明满足条件的AVE问题有2n个解.

先证明矩阵(AD-I)是可逆的. 反之,则齐次线性方程组(AD-I)x=0存在非零解a≠0,使得(AD-I)a=0,从而‖AD‖∞‖a‖∞≥‖ADa‖∞=‖a‖∞,因此‖A‖∞=‖AD‖∞≥1,这与‖A‖∞<γ/2≤0.5<1矛盾. 用|D|表示对矩阵D的每个元素取绝对值,则有|D|=I,令x=Dy,则有|x|=|Dy|=|y|.

考虑方程ADy-y=b,由于‖AD‖∞=‖A‖∞<1,则利用上述结果知ADy-y=b有唯一的正解y*,且y*=(AD-I)-1b. 而ADy-y=b有唯一的正解y*⟺ADy-|y|=b有唯一的正解y*⟺Ax-|x|=b有唯一的(带D模式的)解x*=Dy*.

由于D=diag(d1,d2,…,dn),di=±1,i=1,2,…,n,因此D的模式共有2n个,从而方程Ax-|x|=b共有2n个解,且2n个解可由式x*=D(AD-I)-1b分别计算.

由上述证明易见,该2n个解互不相同.

2 2n个解的算例分析

例1考虑AVE问题:

(2)

经简单计算可得:

例2考虑AVE问题:

(3)

经简单计算可得:

例3考虑AVE问题:

(4)

下面考虑例3中2n个解的分布.

定理7记例3的解为x*(共有2n个互不相同的解),则x*满足

证明: 由于Ax*-|x*|=b,b=(-1,-1,…,-1)T,则有

‖(|x*|-1)‖∞=‖Ax*‖∞≤‖A‖∞‖x*‖∞=0.4‖x*‖∞.

(5)

不妨设

从而式(5)可简化为

(6)

因此

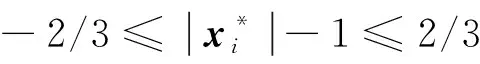
即

3 求解多解AVE问题的注意事项

1) AVE问题是一个不可微问题,不能直接使用传统的梯度类算法(最速下降算法、 各类拟牛顿算法和光滑牛顿法等),即使如文献[16,23]中进行光滑处理后再使用梯度类(或拟牛顿)算法,在给定初始点后,也只能收敛到原问题的一个最优解[24-25]；如何求得上述问题的所有2n个互不相同的解,传统算法则无法实现.

2) 而群体智能算法(如粒子群算法[26]、 差分进化算法[27]和声搜索算法[28]等)是一类随机搜索算法,对目标函数的可微性没有要求,且算法是多点开始的,因此经过多次执行算法就有可能找到AVE问题尽可能多的解.

3) 算法初始可行域的选取一定要包含AVE问题的所有解(防止漏解),只有这样,通过多次执行算法,才有可能找到AVE问题尽可能多的解.

如例3中,由于

⊂[-2,2],i=1,2,…,n,

因此可以选取初始可行域为[-2,2],既能防止漏解,又明确了搜索范围；避免了为求得所有解而选取搜索空间过大,即减少了搜索的盲目性.

4) 2n个解的分布仅与向量b和矩阵A的无穷范数有关,与矩阵A的元素无关.

如例3中,向量b不变,三对角矩阵A的元素变更为

此时,这2n个解的分布仍不变,即对任意一个解,定理7仍成立.

5) 对高维的且有多个解的AVE问题,为了防止计算过程溢出,建议采用稀疏存储方法. 考虑例3,在MatlabR2009a系统中,若不采用稀疏存储,则当维数n=1×104时溢出；若采用稀疏存储,即使维数n=1×107也不会发生溢出现象. 例3中矩阵A的稀疏存储可用如下语句在Matlab系统中生成：

A1=sparse(1∶n,1∶n,0.2,n,n);

A2=sparse(1∶n-1,2∶n,0.1,n,n);

A3=sparse(2∶n,1∶n-1,0.1,n,n);

A=A1+A2+A3.

[1] Rohn J. Systems of Linear Interval Equations [J]. Linear Algebra and Its Applications,1989,126: 39-78.

[2] Rohn J. A Theorem of the Alternatives for the EquationAx+B|x|=b[J]. Linear and Multilinear Algebra,2004,52(6): 421-426.

[3] Mangasarian O L,Meyer R R. Absolute Value Equations [J]. Linear Algebra and Its Applications,2006,419(2/3): 359-367.

[4] Oleg P. On Equivalent Reformulations for Absolute Value Equations [J]. Computational Optimization and Applications,2009,44(3): 363-372.

[5] HU Sheng-long,HUANG Zheng-hai. A Note on Absolute Value Equations [J]. Optim Lett,2010,4(3): 417-424.

[6] Rohn J. On Unique Solvability of the Absolute Value Equation [J]. Optim Lett,2009,3(4): 603-606.

[7] Rohn J. An Algorithm for Solving the Absolute Value Equation [J]. Electronic Journal of Linear Algebra,2009,18: 589-599.

[8] Rohn J. A Residual Existence Theorem for Linear Equations [J]. Optim Lett,2010,4(2): 287-292.

[9] WEI Qing-ju. A Generalized Newton Method and Its Convergence for Absolute Value Equation [D]. Beijing: Beijing Jiaotong University,2009. (魏庆举. 绝对值方程的广义牛顿算法及其收敛性 [D]. 北京: 北京交通大学,2009.)

[10] ZHANG Chao,WEI Qing-ju. Global and Finite Convergence of a Generalized Newton Method for Absolute Value Equations [J]. Journal of Optimization Theory and Applications,2009,143(2): 391-403.

[11] YONG Long-quan,MA Shou-fu. Existent Conditions of Solution to Absolute Value Equations Problem [J]. Journal of Xinxiang University: Natural Science Edition,2010,27(5): 19-21. (雍龙泉,马守富. 绝对值等式问题解的存在性研究 [J]. 新乡学院学报: 自然科学版,2010,27(5): 19-21.)

[12] WANG Ai-xiang,WANG Hai-jun,GONG Cheng. Unique Solvability of Absolute Value Equations [J]. Science Technology and Engineering,2010,10(34): 8501-8502. (王爱祥,王海军,龚成. 绝对值方程的唯一可解性 [J]. 科学技术与工程,2010,10(34): 8501-8502.)

[13] Mangasarian O L. Absolute Value Programming [J]. Computational Optimization and Aplications,2007,36(1): 43-53.

[14] Mangasarian O L. Absolute Value Equation Solution via Concave Minimization [J]. Optim Lett,2007,1(1): 3-8.

[15] Mangasarian O L. A Generlaized Newton Method for Absolute Value Equations [J]. Optim Lett,2009,3(1): 101-108.

[16] Caccetta L,QU Biao,ZHOU Guang-lu. A Globally and Quadratically Convergent Method for Absolute Value Equations [J]. Computational Optimization and Applications,2011,48(1): 45-58.

[17] WANG Ai-xiang,WANG Hai-jun. An Interval Method for Absolution Value Equations [J]. Journal of Guizhou University: Natural Science Edition,2010,27(2): 7-10. (王爱祥,王海军. 绝对值方程的区间算法 [J]. 贵州大学学报: 自然科学版,2010,27(2): 7-10.)

[18] WANG Ai-xiang,WANG Hai-jun,DENG Yong-kun. Interval Algorithm for Absolute Value Equations [J]. Central European Journal of Mathematics,2011,9(5): 1171-1184.

[19] Noor M A,Iqbal J,Khattri S,et al. A New Iterative Method for Solving Absolute Value Equations [J]. International Journal of the Physical Sciences,2011,6(7): 1793-1797.

[20] Noor M A,Iqbal J,Noor K I,et al. On an Iterative Method for Solving Absolute Value Equations [J]. Optim Lett,2012,6(5): 1027-1033.

[21] Mangasarian O L. Absolute Value Equation Solution via Dual Complementarity [J]. Optim Lett,2013,7(4): 625-630.

[22] YONG Long-quan. A New Solution Method for Absolute Value Equations [J]. Science and Technology Review,2010,28(5): 60-62. (雍龙泉. 绝对值等式问题的一个求解方法 [J]. 科技导报,2010,28(5): 60-62.)

[23] YONG Long-quan,LIU San-yang,ZHANG She-min,et al. Smoothing Newton Method for Absolute Value Equations Based on Aggregate Function [J]. International Journal of the Physical Sciences,2011,6(23): 5399-5405.

[24] YONG Long-quan,LIU San-yang,ZHANG Jian-ke,et al. A New Feasible Interior Point Method to Absolute Value Equations [J]. Journal of Jilin University: Science Edition,2012,50(5): 887-891. (雍龙泉,刘三阳,张建科,等. 绝对值方程的一种严格可行内点算法 [J]. 吉林大学学报: 理学版,2012,50(5): 887-891.)

[25] YONG Long-quan. An Iterative Method for Absolute Value Equations Associated with Real Symmetric Matrices [J]. Journal of Southwest University: Natural Science Edition,2012,34(5): 32-37. (雍龙泉. 迭代法求解实对称矩阵绝对值方程 [J]. 西南大学学报: 自然科学版,2012,34(5): 32-37.)

[26] YONG Long-quan. Particle Swarm Optimization for Absolute Value Equations [J]. Journal of Computational Information Systems,2010,6(7): 2359-2366.

[27] YONG Long-quan. Differential Evolution-Simplex Hybrid Algorithm for Absolute Value Equations [J]. Application Research of Computers,2011,28(9): 3327-3329. (雍龙泉. 基于差分进化-单纯形混合算法求解绝对值方程 [J]. 计算机应用研究,2011,28(9): 3327-3329.)

[28] YONG Long-quan,LIU San-yang,ZHANG She-min,et al. A New Method for Absolute Value Equations Based on Harmony Search Algorithm [J]. ICIC Express Letters,Part B: Applications,2011,2(6): 1231-1236.

[29] Noor M A,Iqbal J,Al-Said E. Residual Iterative Method for Solving Absolute Value Equations [J/OL]. Abstract and Applied Analysis,2012:doi: 10.1155/2012/406232.

[30] Hooshyarbakhsh V,Lotfi T,Farhadsefat R,et al. An Iterative Method for Solving Absolute Value Equations [R/OL]. 2012. http://www3.cs.cas.cz/ics/reports/v1145-12.pdf.

[31] Rohn J. An Algorithm for Computing All Solutions of an Absolute Value Equation [J]. Optimization Letters,2012,6(5): 851-856.

[32] WANG Hai-jun,LIU Hao,CAO Su-yu. A Verification Method for Enclosing Solutions of Absolute Value Equations [J]. Collect Math,2013,64(1): 17-38.

[33] Ketabchi S,Moosaei H. Minimum Norm Solution to the Absolute Value Equation in the Convex Case [J]. Journal of Optimization Theory and Applications,2012,154(3): 1080-1087.

[34] Ketabchi S,Moosaei H,Fallahi S. Optimal Error Correction of the Absolute Value Equation Using a Genetic Algorithm [J]. Mathematical and Computer Modelling,2013,57(9/10): 2339-2342.

[35] Ketabchi S,Moosaei H. An Efficient Method for Optimal Correcting of Absolute Value Equations by Minimal Changes in the Right Hand Side [J]. Computers and Mathematics with Applications,2012,64(6): 1882-1885.