曲柄摇杆式飞剪剪刃间隙研究

陈 洁

(中冶南方工程技术有限公司技术研究院)

0 前言

曲柄摇杆式飞剪是冶金生产线上的重要设备，其结构设计的好坏直接影响到被剪带钢的断面质量。设计曲柄摇杆式飞剪时，需要同时满足运动学和动力学条件。许多学者在结构强度、剪刃轨迹等方面进行了研究［1-3］，但极少有研究涉及剪刃间隙的变化。实际上，曲柄摇杆式飞剪在剪切过程中，其剪刃间隙总是发生变化，对于薄带钢而言，这一变化可能导致剪切质量下降甚至产生“卡钢”事故。本文首先应用闭环矢量方程建立飞剪的运动学模型，应用牛顿-辛普森法［4］对剪刃坐标进行求解，在此基础上对剪切区间的剪刃间隙变化情况进行了分析，为剪刃间隙补偿提供理论依据。

1 飞剪结构简介

本文研究的飞剪主要应用在带钢连续处理线上。它布置在机组出口，主要用于分卷、取样剪切、焊缝剪切和废钢剪切。

如图1所示，曲柄摇杆式飞剪可简化为四连杆机构，由曲柄1、上刀架3、下刀架4和机架组成。其中曲柄1为原动件，作旋转运动，下刀架4作摆动，上剪刃2和下剪刃5在垂直方向重合时产生剪切动作。

2 飞剪运动学数学模型

为求得剪切过程中剪刃间隙的变化，必须先求出剪刃在大地坐标系中的位置，本论文首先采用闭环矢量方程求解各连杆的位移参数，然后推导出上下剪刃的坐标，最后求解剪刃间隙。

2.1 飞剪剪切机构的运动学数学模型

将图1所示的飞剪剪切机构抽象为四连杆机构，则可得飞剪剪切机构计算模型。如图2a所示，向量R1～R4分别为飞剪曲柄支座与下刀架支座连线、下刀架、上刀架以及曲柄的向量表示。由于上下剪刃分别固定在上下刀架上，因此由上下刀架的运动学分析结果可推导出上下剪刃的运动学分析结果。以下刀架与机架的铰接点为坐标原点，由该示意图可得到机构的闭环矢量方程:

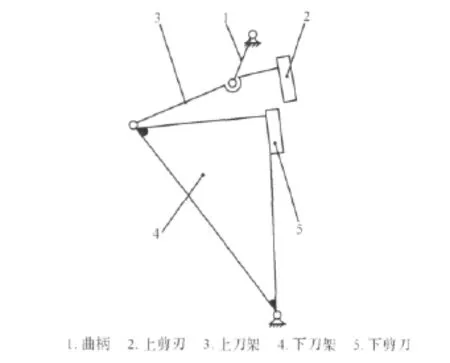
图1 飞剪剪切机构示意图Fig.1 Schematic diagram of flying shear mechanism

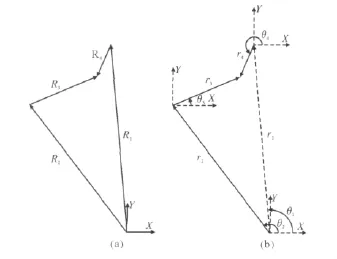
图2 飞剪剪切机构计算模型Fig.2 Calculation model of flying shear mechanism

无论机构运动到什么位置，曲柄与上刀架铰接点始终处于铰接状态，闭环矢量方程 (1)正是从数学上将这一约束关系进行描述。这种描述方式简单直观，且易于求解。

将 (1)式转化为标量形式，其中r1～r2为图2a中各向量的长度，θ1～θ4为这些向量的角度如图2b所示。

(2)式即为飞剪机构的位置方程组。式中r1～r4由图纸可查，θ1为固定值，θ4为主动件曲柄角度，θ2、θ3为未知量，它们随θ4变化而变化。由此可计算出曲柄在任意角度时四连杆机构中上刀架与下刀架所处的角度位置。

飞剪机构的位置方程组为非线性方程组，可以采用牛顿－辛普森法进行求解，具体求解步骤可参考文献［4］。

对于任意给定的曲柄位置角θ4，θ2、θ3求解后，四连杆机构位置即可确定，由于上、下剪刃刚性联接与上、下刀架，因此其位置可由四连杆机构位置确定。上、下剪刃的位置求解模型如图3所示。

图3 上下剪刃的求解模型Fig.3 Calculation equation of upper and lower shear blades

上剪刃与上刀架向量R3之间存在夹角θp3，因此上剪刃在图示坐标系内的向量表达为

其水平和垂直方向坐标为

同理，下剪刃端点处在图示坐标系内的水平和垂直方向坐标为

2.2 剪刃间隙计算

本飞剪上剪刃为平剪刃，下剪刃为V形剪刃，带钢在宽度方向被剪断的过程是从两边向中间进行。如图4a所示，上剪刃的剪切面投影为CD，下剪刃的剪切面投影为AB，上剪刃剪切点为D，下剪刃剪切点在AB上的投影E则沿AB边滑动。对于水平运行的带钢，上剪刃剪切点D接触带钢时，下剪刃剪切点E与D近似保持水平 (考虑带钢厚度)，定义D、E之间的距离为剪刃间隙。为了保证剪切断面平直，必须力求上下剪刃在剪切过程中的间隙维持在一个常数。上下剪刃端点处的运动坐标求出来后，剪刃间隙的求解模型如图4a所示。

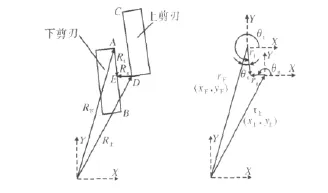
图4 飞剪剪刃间隙计算模型Fig.4 Calculation equation of flying shear's blade clearance

以下刀架与机架的铰接点为坐标原点，由该示意图可得到模型的闭环矢量方程为

将式 (6)转化为标量方程 (图4b)为

2.3 剪刃间隙曲线

以剪刃宽度为2 000 mm，下剪刃V形倾角为0.8度为例，由式 (4)、(5)及 (8)计算出的1/2剪刃宽度范围的剪刃间隙变化曲线如图5所示。

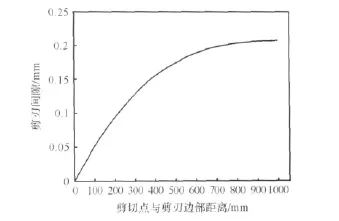
图5 飞剪剪切时剪刃间隙变化曲线Fig.5 Changing curve of blade clearance while flying shear is working

由图5可知，本飞剪剪切时，上下剪刃的间隙最大为0.2 mm，且发生在下剪刃V形的最低点。因此，设计上剪刃座时，可参考图5剪刃间隙变化曲线进行剪刃间隙补偿方案设计，以保证剪切断面质量。

3 结论

曲柄摇杆式飞剪正常工作除要满足载荷条件外，还需满足运动条件，本文利用闭环矢量方程建立了某曲柄摇杆式飞剪的运动学模型，对剪刃端点坐标和剪刃间隙进行求解，为剪刃间隙补偿提供了理论依据。所采用的方法简单明了，对分析类似结构的飞剪具有借鉴意义。

［1］陈鹏，陈幼南，徐少平.施罗曼飞剪机构的解析综合与程序设计 ［J］.湖北工学院学报，2008，18(2):126－128.

［2］丁文红，何光逵.施罗曼飞剪动力学分析.武汉钢铁学院学报 ［J］.1993.16(4):384－390.

［3］陈洁.基于Matlab的曲柄摇杆式飞剪运动学分析研究.冶金设备 ［J］.2009(6):39－41.

［4］John Gardner，机构动态仿真 －使用MATLAB和SIMULINK［M］.西安交通大学出版社，2002.