OUTPUT MAXIMIZATION CONTROL FOR VSCF WIND ENERGY CONVERSION SYSTEM USING EXTREMUM CONTROL STRATEGY

FuDafeng（付大丰），Ma Yundong（马运东）

（College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China）

INTRODUCTION

Nowadays one of human′s endeavors is to cope with the energy crisis.Because wind power is free，clean and endless，it is a very good choice.Furthermore，the cost of the electricity produced by wind turbines is fixed once the plant has been built and it has already reached the point where the cost of the electricity produced by wind is comparable with that produced by some of the conventional and fossil based power plants.Therefore，compared with other renewable energy technologies，wind energy conversion system（WECS）is the most promising one.

Wind is highly variable，both in space and in time.The importance of this variability becomes critical since it is amplified by the cubic relation of the available energy.The speed-control criterion leads to two types of WECS：Fixed-speed and variable-speed wind turbines. Variable-speed wind turbines are currently the most used WECS.Compared with fixed-speed wind turbines，their advantages are numerous.First of all and most importantly，the decoupling between the generating system and the grid frequency makes them more flexible in terms of control and optimal operation.And the high controllability offered by the variable-speed operation is a powerful advantage in achieving higher wind energy penetration levels［1－2］.Moreover，the variable-speed operation allows the rotational speed of the wind turbine to be continuously adapted （accelerated or decelerated）in such a manner that the wind turbine operates constantly at its highest level of aerodynamic efficiency.Furthermore，variable-speed operation allows the use of advanced control methods，with different objectives：Reduced mechanical stress，decreased acoustical noise，increased power capture，and so on［3］.

Obviously，how to realize the output maximization control of WECSs is a challenging problem. Therefore，advanced automatic control methods are imperatively required.The maximum power point tracking （MPPT）means roughly to extract the maximum power available in the wind stream，irrespective of the wind regimes，and takes place in the partial-load region.In fact，the traditional MPPT approach employs the hillclimbing method for dynamically driving the operating point to the optimal regimes characteristic（ORC）.In order to obtain gradient estimations of some measurable variables，some probing signals are used［4－5］.And the traditional MPPT approach has some drawbacks.The main ones are the significant estimation errors and important high-frequency power fluctuations，which will influence the reliability of the system.In order to cancel the impact of the above effects，the MPPT algorithms employing fuzzy control techniques are used［6－8］.Although the techniques are easy to be extended and more flexible，they should have much more requirement on the system model.

Extremum seeking control（ESC）is one of the methods to maximize or minimize a cost function which denotes efficiency，benefit，loss，and so on［9］.Thus，a new approach to MPPT employing an extremum search algorithm is proposed in the paper.The algorithm uses the wind turbulence as a probing signal to obtain gradient estimations of some measurable variables，such as the electrical power，the wind speed，the rotational speed，and so on.Thus it can drive the operation point to ORC dynamically.

In this paper，the operation characteristics of WECS and the wind speed model are given，and the traditional MPPT approach to WECS is ana-lyzed.Moreover，a new approach to MPPT based on the extremum seeking control principles is presented.The numerical simulations are realized using MATLAB and the effectiveness of the proposed scheme is validated under different operating conditions by simulation results.

1 OPERATION CHARACTERISTICS OF WECS

1.1 Operation characteristics of wind turbine

As shown in Fig.1，the wind turbine operates from the cut-in wind speed to the cut-out wind speed with different dynamics.That is to say，four zones may be identified in the static operation of WECS depending on the wind speed.

Fig.1 Output power vs.wind speed characteristic

Obviously，the mechanical power PWTextracted by a wind turbine must be limited to the rated one PNin the full load zone.Thus，the interest focused on the partial load zone is output energy maximization control.

The mechanical power PWTis expressed as

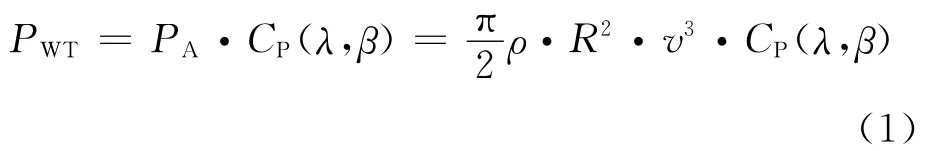
where PAis the total power of a delimited moving mass of air，ρthe air density，Rthe blade radius，vthe wind speed，and CP（λ，β）the power coefficient defining the aerodynamic efficiency of the wind turbine rotor.Usually it is a function of the tip speed ratioλand the blade pitch angleβ.

Because of the fixed-pitch wind turbine，βis constant here.The tip speed is defined as the ratio between the peripheral speed of the blades and the wind speed.It is denoted byλand computed as

whereΩlis the rotor rotational speed.

Fig.2presents the CP－λperformance curve.For control purposes，the useful information arising from the Fig.2is the fact that the power conversion efficiency has a well determined maximum for a specific tip speed ratio，denoted by λOPT.

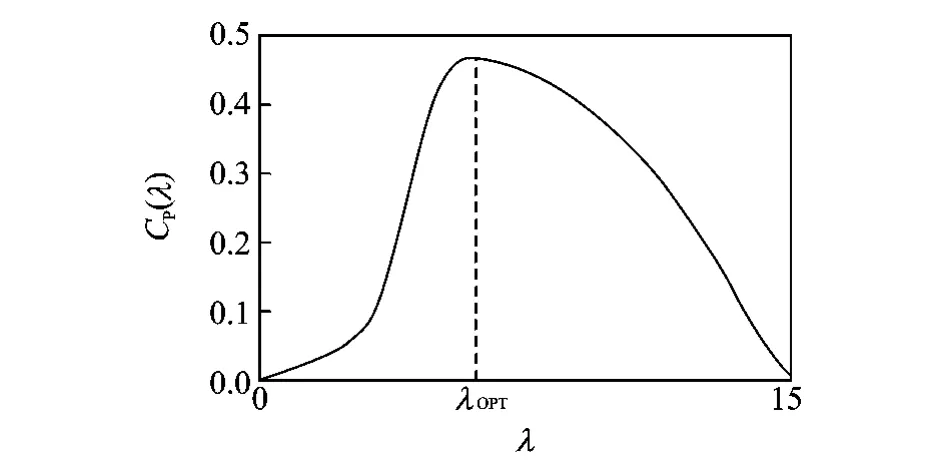
Fig.2 CP－λcurve of typical horizontal axis wind turbine

The corresponding power characteristics parameterized by the wind speed are shown in Fig.3.Obviously，for each wind speed，there is a certain rotational speed at which the power curve of a given wind turbine has a maximum （CPreaches its maximum value）.And all these maxima compose what is known in the literature as the optimal regimes characteristic（ORC）.

Fig.3 Power characteristics parameterised by wind speed

Therefore，the energetic optimization is equivalent to trackingλOPTirrespectively of the wind speed.In the case of the fixed-pitch wind turbines this can be achieved by appropriately torque／rotational speed controlling the electric generator［10］.

1.2 Wind speed modeling

From a system point of view，the wind speed represents the main exogenous signal applied to WECS and determines its behaviour.Its erratic variation，highly dependent on the given site and on the atmospheric conditions，makes the wind speed quite difficult to model.Reviewing literatures，the wind speed model used in current dynamic simulation for VSCF wind turbine is usually reduced to three kinds of typical wind speed，that is，gust，random wind and gradient wind.This approach is more in line with reality.In view of focusing on the energetic optimization of the energy conversion system，wind speed is modelled in the literature as a non-stationary band-limited random process，yielded by superposing two components［11］

where vs（t）is the low-frequency component（or seasonal component）describing long term variations and vt（t）the turbulence component corresponding to fast and high frequency variations.In a word，vs（t）determines the average position of the operation point on the wind turbine characteristic and vt（t）generates the high frequency variations around this point.

The turbulence is mathematically described as a zero average normal distribution，whose standard deviation，σ，depends on the current value of the hourly average，vs（t）.The turbulence intensity is a measure of the global level of turbulence，depending on the ground surface roughness and is defined as

Here Fig.4presents a wind sequence with the average speed of about 7m／s and a medium turbulence intensity of I＝0.15，obtained by using the von Karman spectrum in the IEC standard.

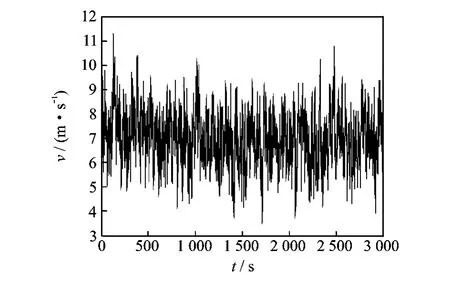
Fig.4 Model of wind speed（v＝7m／s，I＝0.15）

2 MPPT BASED ON ESC

While the aerodynamics and drive train models are not fully available，that is to say，only few constructive parameters are known and few variables are available for measure，the new version of MPPT based upon poor knowledge about the system must be developed.But the basic idea of any MPPT algorithm is to maintain the optimal operating point，denoted as

2.1 Traditional MPPT approach

Fig.5illustrates the traditional MPPT approach employing the hill climbing method.Therefore，the operation point position and its moving trend （the sign of∂PWT／∂Ωl）determine the wind turbine speed reference together.The wind turbine power PWTis estimated based on the measured active power P.Also，the rotational speedΩlof low speed shaft（LSS）is estimated from measuring the generator speedΩh.

Fig.5 Principle of traditional MPPT

The significant estimation errors and the important high frequency power fluctuations are the two main drawbacks of this method，which are harmful for the overall reliability.In order to avoid the first drawback，one can use heuristic methods needing wind speed estimation，along with power coefficient curve identification［12］.As for the second drawback，some extensions of the MPPT algorithms，for example，fuzzy control techniques，lead to more flexible，but also quite context dependent controllers［8］.

2.2 New MPPT approach based on adaptive extremum control

Extremum control strategy （ECS）has been evolved since 1950along with optimization theory，adaptive control theory and nonlinear control theory.And several design methods have been discussed to construct ECS in the last few years.Especially，Krstiˇc′s method using averaging technique attracts a lot of interest［9］.

（1）Principle of single-parameter extremum seeking control

The ESC method relies upon finding the extremum of some unimodal function dynamics by exciting the plant with sinusoidal probing signals.The basic idea of this control method is illustrated in Fig.6，where the controller performs a modulation／demodulation operation and its output has a harmonic component called the probe signal.It usually contains a washout filter，a demodulator，a low pass filter and an integrator for obtaining the average component of the control input，and a summation with the probing signal block.

Fig.6 Principle of single-parameter extremum seeking control

The power characteristic has a maximum at λOPTfor each wind speed in the partial load region.Then the Taylor series of this function around its maximum，CP（λOPT），is denoted as

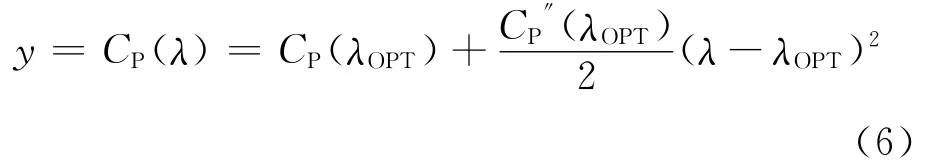
The purpose of the algorithm is to makeλλOPTas small as possible，so that the output yis driven to its maximum CP（λOPT）.The perturbation signal asinωt fed into the plant helps to get a measure of gradient information of the map CP（λ）.Parameter＾λin Fig.6denotes the estimate of the unknown optimal inputλOPT.Let~λ＝λOPT－＾λdenote the estimation error，thus

Replacing Eq.（7）in Eq.（6）and expanding it further can result in that

Note thatλOPTis constant and the last two rows are high frequency signals.When the two rows pass through an integrator，we have

Since kCP″＞0，this is a stable system.Thus concluding that~λ→0，converges to within a small distance ofλOPT.Therefore，the searching process is convergent.The excitation frequency，ω，must be sufficiently large to ensure stability of the closed loop system，and the washout filter parameter，h，depends on this frequency［9］.

（2）New MPPT method

According to the above analysis，this principle can be used in a WECS optimal control application.Thus，an already existing perturbation，wind turbulence，is used here instead of sinusoidal probing signals.In this case，the modulation process is naturally achieved by means of high frequency（non harmonic）wind speed variations.

The stated scope of the control can be achieved by changing the tip speed ratioλ.And the linearized variation ofλis expressed as

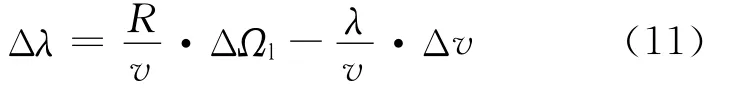
Based on the basis of Eq.（3），Δv may be simplified asΔvt.At the time，ΔΩlis neglected because the time interval is very small.

Thus

In Eq.（12），Δλcan be used instead of sinωt feeding the system because the wind turbulences have high frequency variations.As a result，they induce some power coefficient variations，ΔCP，which are non harmonic，but have a bounded spectrum.

From the ESC principle discussed above，the integrator input is expressed as

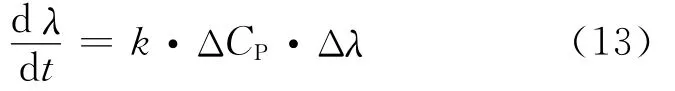
Consideration of the change of wind speed is a random process，and the separation of sinusoidal exciting signals is the key and difficult task.In this paper，the discrete Fourier transform（DFT）is used for extracting the phase of each harmonic component ofλ（t）and CP（t），and then computing the phase lag of each component.An average of these values gives the angle denoted byθ（t），which contains the average position information of operation point.If operation point is on the left（rising）slope of the CPcurve，the values ofθ（t）will get closer to 0.Otherwise，the values ofθ（t）will get closer toπin the right case.This is illustrated in Fig.7.

Fig.7 Relationship between operation point andθ

Here the applied method is based upon deducing the average phase shift，denoted byθ（t）.As a result，the position of operation point will be separated into two zone characterized byπ／2.

（3）Control law

Fig.8presents the control structure including an information processing block and a rotational generator speed reference block［13］.

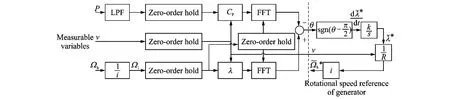
Fig.8 Control structure of new MPPT appoach

From Fig.8，CP（t）andλ（t）are obtained using the electrical power with wind speed and the rotational speed with wind speed respectively.These signals are fed to a FFT algorithm for obtaining their phase spectrum and the corresponding average position signal，θ（t）.

On the right side of Fig.8，the augment or reduction of tip speed reference can be achieved by integrating a nonlinear function of average phase information，sgn（θ－π／2）.Finally the rotational generator speed reference is obtained.

3 SIMULATION RESULT AND ANLYSIS

The numerical simulation and result analysis are given in the section.A 6kW fixed-pitch horizontal-axis variable-speed WECS operating in the partial load region is used as case study for the above proposed MPPT approach.The rotor of turbine and the squirrel-cage induction generator（SCIG）are coupled by a rigid drive train.Its main parameters are given as follows.

Turbine parameters：R＝2.5m，vs＝9m／s，vr＝15m／s.

SCIG parameters：Rs＝1.265 Ω，Rr＝1.43Ω，Lm＝0.139 7H，Ls＝0.145 2H，Lr＝0.145 2H，P＝2.

The power coefficient can be described by a polynomial function of the tip speed ratio，λ［14］，that is

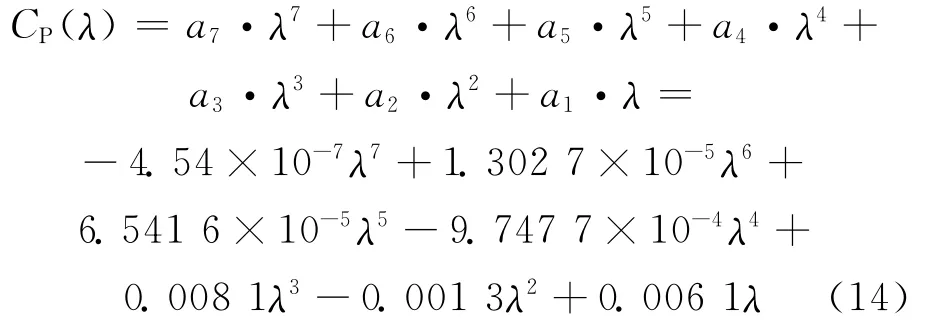
Therefore it has the following optimal pa-rameters

The simulations by MATLAB／SIMULINK only concern the partial load region for medium wind turbulence and no wind gusts.

In Fig.9，the CP－λperformance curves based on the traditional MPPT approach vs.the new version of MPPT using ECS are compared.As a result，the standard deviation of the power coefficient in Fig.9（b）is much smaller than that in the case of the classical MPPT control on the left.The controller gain kin Fig.9（b）is 0.03.

Fig.9 CP－λ performance curves based on two MPPT approaches

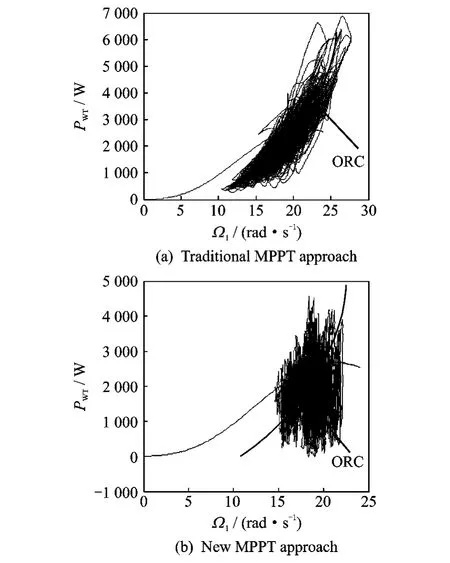
Fig.10 Energy optimization curves based on two MPPT approaches

Similarly，in Fig.10the energy optimization curves using speed-power plane based on the two MPPT approaches are compared.Obviously，the operation point distribution around ORC in Fig.10（b）on the right is more easy to be remarked than the case in Fig.10（a）on the left.ORC is explained in Fig.3.Therefore，compared with the classical MPPT version，the new MPPT version based on ESC has a better performance.

Fig.11shows the simulation results with different values of the control gain k.From Fig.11，it can be deduced that the control gain kis smaller，and the standard deviations of the CP－λperformance curves are smaller.Therefore if the system has been in steady-state regime，better performance can be realized by a small value of k.

4 CONCLUSION

The paper deals with a wind power system using a variable-speed wind turbine driving a squirrel-cage induction generator connected to the grid through power converter.

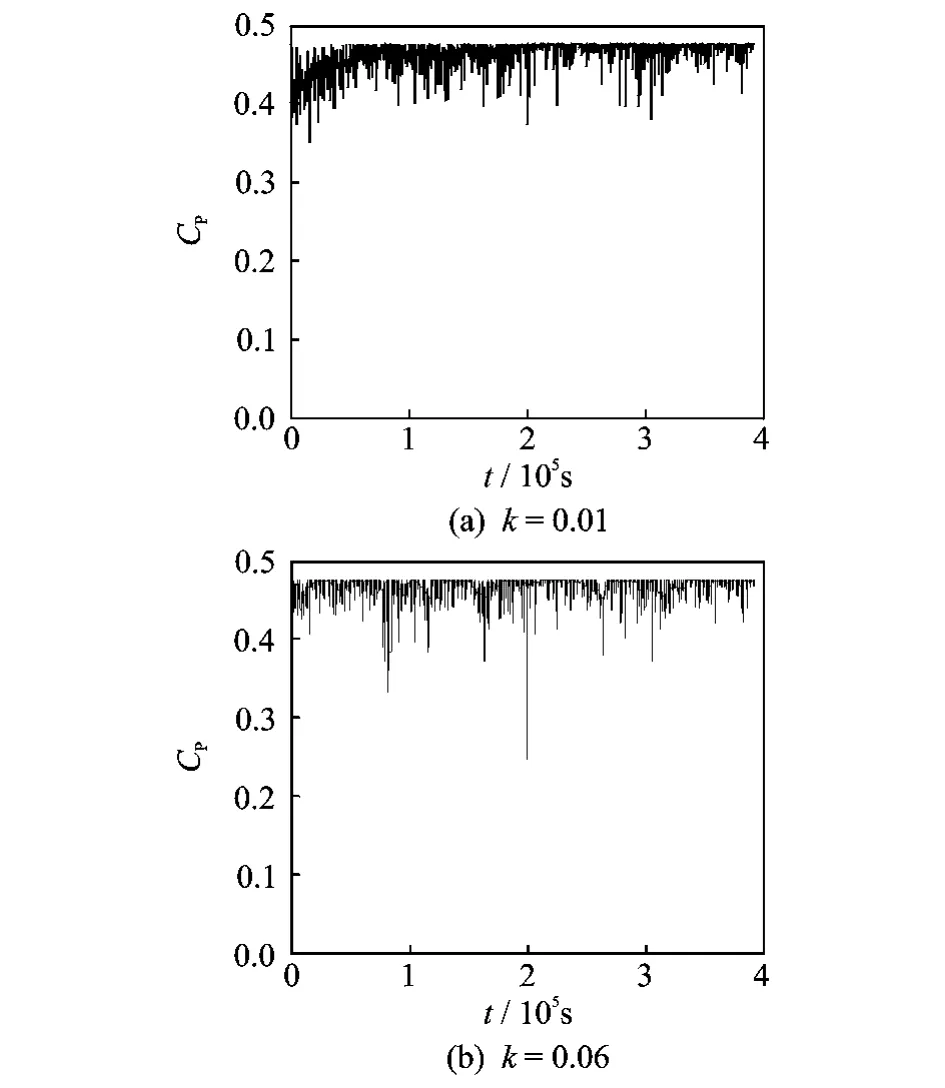
Fig.11 Influence of control gain kon CP－λperformance curves based on new MPPT approach

Classical MPPT has some drawbacks such as requiring real time computation of gradients.A new MPPT control approach based on the extre-mum seeking control for variable-speed WECS is presented in this paper.When the plant is not sufficiently and precisely known，the new approach proves its efficiency.Moreover，the control strategy has higher flexibility because the information ofθ（t）is included in the control gain k.

Compared with the classical MPPT，the proposed MPPT approach shows better control performances.This is validated by simulations results in MATLAB／SIMULINK.The most valuable feature of the presented approach is the use of minimal knowledge about the state and parameters of system.And it has the advantage of employing very few parametric and feedback information in the controller construction.

［1］ Fu D F，Xing Y.Study on linear dynamic model and analysis of operating characteristics of high-power VSCF wind energy conversion system ［C］∥ World Non-Grid-Connected Wind Power and Energy Conference.Nanjing，China：IEEE，2009：1-6.

［2］ Søensen P，Hansen A D，Iov F，et al.Wind farm models and control strategies［R］.Technical Report RISØ-R-1464（EN）.Roskilde，Denmark：RISØ Na-tional Laboratory，2005：12-16.

［3］ Burton T，Sharpe D，Jenkins N，et al.Wind energy handbook ［M］.New York：John Wiley ＆ Sons，2001：120-125.

［4］ Datta R，Ranganathan V T.A method of tracking the peak power points for a variable speed wind energy conversion system ［J］.IEEE Trans on Energy Conversion，2008，18（1）：163-168.

［5］ Wang Q，Chang L.An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems［J］.IEEE Trans on Power E-lectronics，2004，19（5）：1242-1249.

［6］ Hong Y Y，Lua S D，Chiou C S.MPPT for PM wind generator using gradient approximation ［J］.Energy Conversion and Management，2009，50（1）：82-89.

［7］ Zeng Q R，Chang L C，Shao R M.Fuzzy-logic-based maximum power point tracking strategy for PMSG variable speed wind turbine generation systems［C］∥Electrical and Computer Engineering. Canada：［s.n.］，2008：120-126.

［8］ Abo-Khalil A G，Lee D C，Seok J K.Variable speed wind power generation system based on fuzzy logic control for maximum output power tracking ［C］∥Proceedings of 2004IEEE 35th Annual Power Electronics Specialists Conference.Aachen，Germany：IEEE，2004：2039-2042.

［9］ Ariyur K B，KrstiˇcM.Real-time optimization by ex-tremum seeking control ［M］.USA： Wiley-Interscience，2003：12-15.

［10］Pen～a R S，Cardenas R J，Asher G M，et al.Vector controlled induction machines for stand-alone wind energy applications ［C］∥Proceedings of the IEEE Industry Application Annual Meeting.Rome，Italy：IEEE，2000：1409-1415.

［11］Bianchi F，De Battista H，Mantz R J.Wind turbine control systems：Principles， modelling and gain scheduling design［M］.London：Springer，2006：169-175.

［12］Farret F A，Pfitscher L L，Bernardon D P.An heuristic algorithm for sensorless power maximization applied to small asynchronous wind turbogenerators［C］∥Proceedings of the IEEE International Symposium on Industrial Electronics.Cholula，Mexico：IEEE，2000：179-184.

［13］Munteau I，Bratcu A I，Ceang E.Wind turbulence used as searching signal for MPPT in variable-speed wind energy conversion systems［J］.Renewable Energy，2009，34（1）：322-327.

［14］Miller N W，Price W W，Sanchez-Gasca J J.Dynamic modelling of GE 1.5and 3.6wind turbine generators［R］.Technical Report，Power Systems Energy Consulting， General Electric International.Schenectady，USA，2003：1-7.