MINIMUM ATTRIBUTE CO-REDUCTION ALGORITHM BASED ON MULTILEVEL EVOLUTIONARY TREE WITH SELF-ADAPTIVE SUBPOPULATIONS

Ding Weiping（丁卫平），Wang Jiandong（王建东）

（1.College of Computer Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.State Key Laboratory for Novel Software Technology，Nanjing University，Nanjing，210093，P.R.China）

INTRODUCTION

Attribute reduction is one of the important topics of rough set theory，which helps us to find out the minimum attribute set and induce minimum length of decision rules inherent in an information system［1］.It has gained considerable importance，with numerous applications in diverse areas of research，especially in data mining，knowledge discovery， and artificial intelligence［2－3］.Therefore a fast and efficient attribute reduction algorithm is especially important for huge data sets.However，the problem of finding the minimum attribute reduction set is more difficult and has been proven to be an NP-hard problem by Wong and Ziarko［4］.The high complexity of this problem has motivated a few investigators to apply some heuristic evolutionary algorithms（EA）to find near-optimal solutions［5－7］.But classical EA （e.g.genetic algorithm （GA），ant colony optimization（ACO），particle swarm optimization （PSO），and shuffled frog-leaping algorithm（SFLA））often suffers from premature convergence because of the loss of population diversity at the early stage.Moreover，each performance deteriorates rapidly as the increasing complexity and dimensionality of the search space so that thousands of seconds may be required to deal with it.The experimental results of these evolutionary algorithms still can not satisfy the attribute reduction of large-scale complex attribute sets.Therefore these algorithms are usually not quite effective in the sense that the probability for them to find the minimum attribute reduction in a large information system appears to be lower.

Cooperative co-evolutionary algorithm（CCEA）introduced by Potter and De Jong［8］is a natural model by a divide-and-conquer approach，which divides the complex swarm into subpopulations of smaller size and each of these subpopulations is optimized with a separate EA.Cooperative co-evolution guides evolution towards the discovery of increasingly adaptive behaviors，in which each subpopulation′s fitness is determined by how well it works with the other subpopulations in producing a complete object.Therefore it has its potential application importance for maintaining diversity and mutual adaptation amongst subpopulations.The concept of evolving subcomponents of a problem independently and co-adaptively sounds natural and attractive，which further enlightens us to study some efficient co-evolutionary algorithms，especially for the NP-hard solution.

As we all know the critical step of CCEA is the problem decomposition. An ideal CCEA should decompose a large problem into subcomponents where the interdependencies of decision variables among different subcomponents are minimal.But there is almost no prior information about how different decision variables are interacting.It turns out there would be a major decline in the overall performance of traditional CCEA，when the tight interactions exist among different attribute decision variables.Therefore in the recent years some effective algorithms and frameworks for decompositions of variable interdependencies have been proposed：DECCG［9］relies on random grouping of decision variables into sub-components in order to increase the probability of grouping interacting variables.MLCC［10］which extends DECCG employs both a random grouping scheme and adaptive weighting technology for decomposition and co-adaptation of subcomponents.CCEAAVP［11］partitions the non-separable variables into subpopulations based on the observed correlation matrix and does not require some priori partition rules.DECCD［12］divides population into predetermined equally-sized subpopulations according to their corresponding delta values.DECCDML［12］which is the variant of DECCD uses a new uniform selection for self-adapting subcomponent sizes along with more frequently random grouping.During tackling the crucial problem decomposition issue，the algorithms may allow for capturing the interacting attribute decision variables and group them in one single subpopulation，but the decomposition strategy often depends on the interacting of problems and thus becomes hard to choose.Therefore the self-adaptation of co-evolving subcomponents is difficult to achieve successfully.

The purpose of this paper is to investigate an efficient minimum attribute reduction algorithm（called METAR）based on multilevel evolutionary tree with self-adaptive subpopulations.A model with hierarchical self-adaptive evolutionary tree is designed to divide attribute sets into subsets with the self-adaptive mechanism according to their historical performance record.Since this model can help to produce the reasonable decompositions by exploiting any correlation and interdependency between interacting attribute subsets，the proposed algorithm can self-adapt the subpopulation sizes and capture the interacting attribute decision variables in order to group them together in one subpopulation.Each of these subpopulations is optimized with a separate EA.Extensive computational studies are carried out to evaluate the performance of the proposed algorithm on a large number of benchmark functions，UCI datasets and magnetic resonance images（MRI）.The simulation result shows the proposed algorithm has superior performance for minimum attribute reduction.

1 RELATED DEFINITIONS

In rough set theory，an information system，which is also called a decision table，is defined as S＝（U，A，V，f），where U，called universe，is a nonempty set of finite objects；A＝C∪Dwhere C is the set of condition attributes and Dthe set of decision attributes；Vis a set of values of attributes in Aand f：A→Va description function［2－3］.

Definition 1 For any R⊆C，there is an equivalence relation I（R）as follows

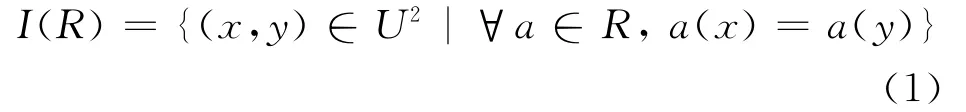
If（x，y）∈I（R），then xand yare indiscernible by attributes fromR.The equivalence classes of the R-indiscernibility equivalence relation I（R）are denoted as［x］R.

Definition 2 Let X⊆U，Rbe binary equivalence relation defined on a universal set U，soRX can be defined as the union of all equivalence classes in X／Rthat are contained in X，such as

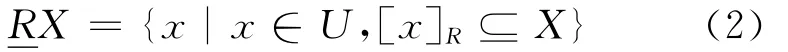
RXcan be also defined as the union of all equivalence classes in X／Rthat overlap with X like the following equation

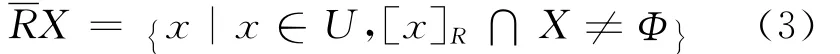
Rough set RXcan be represented with the given setΧas RX＝（RX，RX）.

Definition 3 The C-positive region of Dis the set of all objects from the universe U which can be classified with certainty into classes of U／Demploying attributes fromC，that is

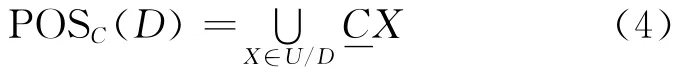
Definition 4 The degree of dependency γP（D）is used as a criterion for the attribute selection as well as a stop condition，defined as follows

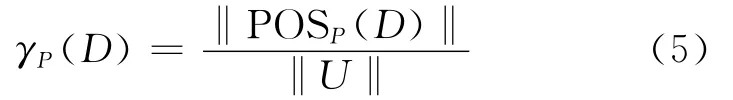
Definition 5 A given decision table may have many attribute reductions，and the set of all reductions is defined as

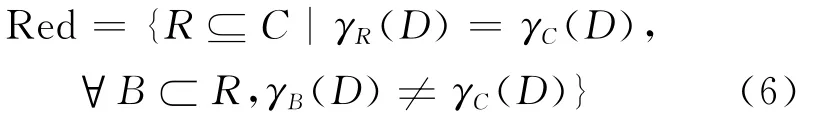
The goal of attribute reduction is to find a reduction with minimum cardinality.An attempt is made to locate a single element of the minimum reduction set

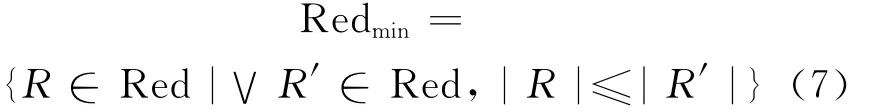
The intersection of all reductions is called the core，the elements of which are those attributes that cannot be eliminated.The core is defined as

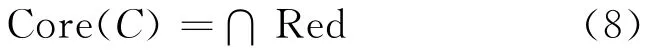
2 ATTRIBUTE REDUCTION BASED ON MULTILEVEL EVOLUTIONARY TREE

2.1 Framework of multilevel evolutionary tree

A novel multilevel evolutionary tree model is proposed to decompose interacting decision variables of attribute sets into self-adaptive subpopulations in this section.This evolutionary tree can self-adapt the subpopulation sizes among its different sub-trees，and it can be better used to capture the interacting attribute decision variables and help to produce the better satisfactory reasonable decompositions by exploiting some correlation and interdependency between interacting attributes subsets.The main framework of multilevel self-adaptive evolutionary tree is designed as Fig.1.

Initially，all evolutionary individuals are arranged in the nodes of an original multilevel evolutionary tree so that each node of tree contains exactly one evolutionary individual.Each inner branch is looked as an evolutionary subpopulation which is only demanded to have the same number of nodes.The evolutionary tree is defined by the height h，the branching degree di，（i.e.，the number of children of each sub-tree），and the total number of nodes mof the tree.For example，in Fig.1（a），h＝3，D＝｛d1，d2，d3｝＝｛4，4，4｝，m＝16and in Fig.1（b），h＝4，D＝｛d1，d2，d3｝＝｛6，3，3｝，m＝16.The tree contains two types of entities.One is ordinary individuals，denoted by white dots，which are the basic independent individuals.There is no cooperation mechanism but competi-tion mechanism among them.The other is the elitist individuals represented by black dots，which are the best children nodes.Each branch of the tree is represented as a subpopulation highlighted as broken line in Fig.1（a）.

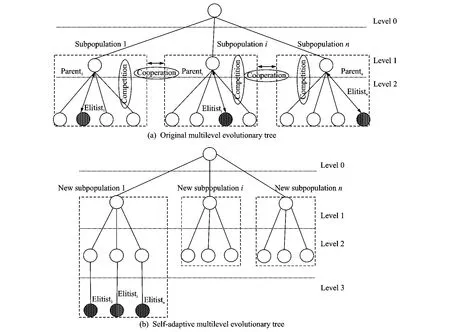
Fig.1 Framework of multilevel self-adaptive evolutionary tree model

In order to give the elitist in the respective subpopulation a high influence，individuals will be compared by their fitness in the evolutionary tree.In every iteration，every Parentiin Subpopulationiof the tree is compared with the best children node Childrenbesti（namely Elitisti）found in all individuals of sub-tree.If f （Elitisti）＜f（Parenti），the elitist node of this sub-tree will be moved to the next lower level in Fig.1（b）.These comparisons are performed starting from the top of the evolutionary tree and then proceeding in a breadth-first manner down each level of evolutionary tree.Through this run，the degree of left branching diis gradually increased，but the degree of right branching diis slowly decreased.This evolutionary tree is traversed starting from the root node.The selected elitists of each subpopulation will be evenly appended one by one at the bottom from the left sub-tree to right one.The procedure is continued until all elitists in the penultimate level are reinserted.As the result，new different subpopulations are reformed.The diwill be a set used as the decomposed size of attribute sets in which the number descends，and left subpopulation contains more elitists which enhance the global optimization performance.For example，in the self-adaptive multilevel evolutionary tree of Fig.1（b），the new branching degree size of each subpopulation is the set D＝｛6，3，3｝.

Only individuals originally exist in the evolutionary tree.Elitist individuals and decomposition subpopulations are created dynamically by the mechanisms of self-adaptive competitive and cooperative co-evolution.When the competitive co-evolution is applied，individuals on all levels of a sub-tree，if any，are mixed together，and two kinds of entities，ordinary individuals or elitist individual，are partitioned by the proportion of fitness to form a new subpopulation.When the cooperative co-evolution is applied，selected elitist of each subpopulation shares its ability of better decomposition experience with two nearest elitists of subpopulations.Then different subpopulations will evolve through their respective elitists as to strengthen the sharing ability of their better decomposition experience for interacting attributes subsets.This process is described in Fig.1（a）.

During the repeated procedure of multilevel evolutionary tree，this strategy of removing the best elitists of subpopulations is proved to provide better results.The reason why it is better to remove with the best node could be that the removed elitists will be appended to the bottom of the evolutionary tree and have good chances to share their better ability of decomposition experience for interacting attribute subsets，which is contributed to the elitists search process.In spite of the dynamic multilevel of the evolutionary tree，the new formed sub-trees concentrate the search on different regions of the attribute subsets，so that it achieves the better performance of coordinating exploration and exploitation.

The advantage of multilevel evolutionary tree is to automatically decide to select the elitists，because selection is driven by the fitness of individuals on subpopulations，and they have been self-adapted from low level to high level.Thus，apart of left evolutionary sub-trees develop to the most appropriate level and contain most elitists.As a result，superior performance of initial decomposed subpopulations can be used to exploit the correlation and interdependency between interacting attribute subsets，and the balance between the effectiveness and efficiency of the search-optimizing is better achieved.

2.2 Minimum attribute reduction optimization model

A reduction with minimum cardinality is called minimum attribute reduction.It can be formulated as a nonlinearly constrained optimization model as follows.

Let ｛0，1｝mbe the m-dimensional Boolean space andξa mapping from ｛0，1｝mto the power set 2Csuch that

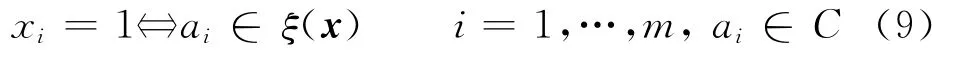
Then，Eq.（7）can be reformulated as the following constrained binary optimization model

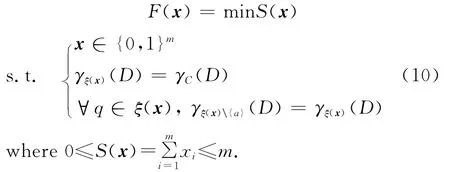
Given a vector x＝｛x1，x2，…，xm｝∈｛0，1｝m，if it is a feasible solution to Eq.（6），its corresponding subset of attributesξ（x）is a reduction.Furthermore，if it is an optimal solution to Eq.（10），thenξ（x）is a minimum attribute reduction.

2.3 Proposed METAR algorithm

According to the model of attribute reduction and the framework of multilevel evolutionary tree，METAR is presented and its flowchart is described in Fig.2.A decomposer of attribute sets is selected from the subpopulations based on the above multilevel evolutionary tree.As considering the superiorities of quantum-behaved evolutionary algorithms，here we prefer using the QPSO［13］as the attribute sets optimizer.With such a mechanism，the METAR algorithm is self-adaptive to capture the interacting attribute decision variables and group them together in one subpopulation.Therefore it will be extended to better performance in both quality of solution and competitive computation complexity for minimum attribute reduction.

The main key steps of the METAR algorithm are summarized as follows：

Input： An information system T ＝（U，C∪D，V，f） ，the set Cof condition attributes consists of mattributes，and other relative parameters.

Output：Minimum attribute reduction Redmin.

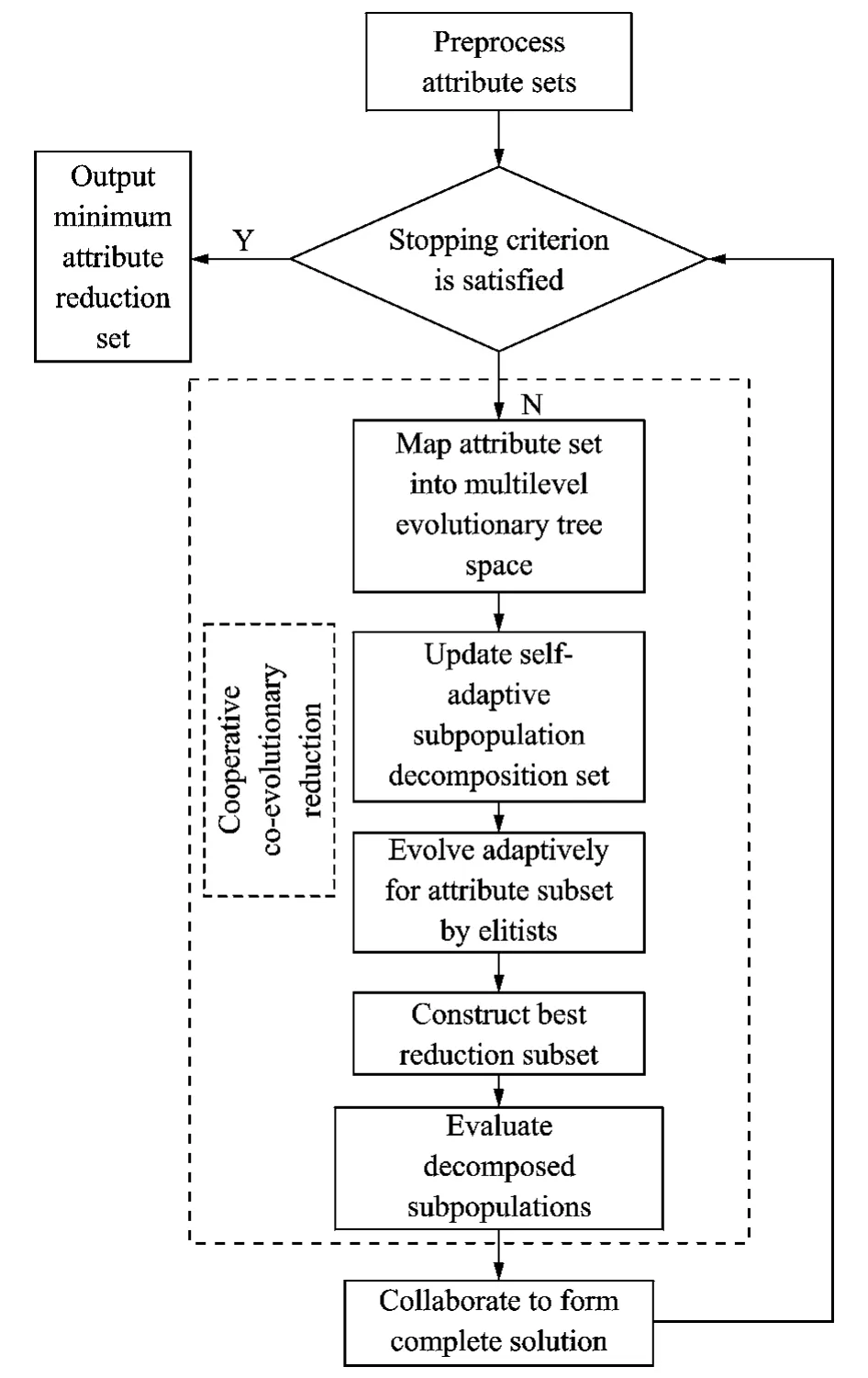
Fig.2 Flowchart of METAR algorithm

Step 1 Compute attribute core Core（D）of attribute reduction sets by using the discrimina-tion matrix.IfγR（D）＝γC（D），then Core（D）is the minimum attribute reduction set，Redmin←Core（D），else go to Step 2.

Step 2 Ensure Core（D）≠REDminaccording to Step 1.Because Core（D）∈Red，Core（D）is not involved the searching optimization，the dimension of attribute sets is H＝｜D｜－｜Core（D）｜.

Step 3 Calculate the weight of each attribute qjby the formula：Weightj＝rcore（c）－qj－rcore（c）.

Step 4 Map each condition attribute into corresponding node of multilevel evolutionary tree，and limit the domain for each node into the defined reduction space ［0，1］by the following

Step 5 Let ｛0，1｝mbe the m-dimensional Boolean space andξa mapping from ｛0，1｝mto the power set 2Cas xi＝1⇔ai∈ξ（x）.（ai∈C，i＝1，2，…，m）in order to fit for the optimization model（i.e.Eq.（10））.

Step 6 Construct a set of population sizes D＝｛d1，d2，…，dt｝by self-adaptive co-populations with multilevel evolutionary tree.

Step 7 Create a performance record list R＝｛r1，r2，…，rt｝.Each di∈Dis connected to ri∈R.Here riis set to 1initially，and will be updated according to

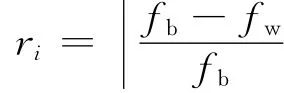
where fbis the Elitisti′s fitness of this subpopulation and fwthe worst fitness.

Step 8 Compute the decomposer probabilities in the decomposer set as follows

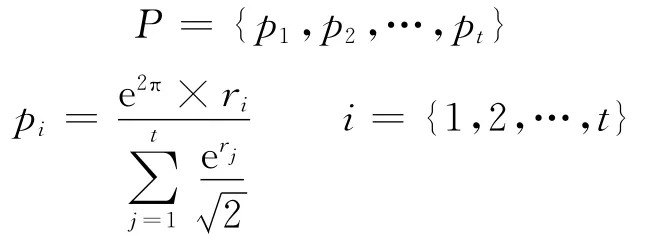
Pwill provide a rather high probability to select the decomposer with the best performance in the multilevel evolutionary tree.

Step 9 Decompose the attribute sets into m×（Sub-attribute）ibased on the group size siaccording to the better decomposer probability pi.

Step 10 Set G＝｛g1，g2，…，gm｝，and each gjrepresents a subcomponent of the decomposed attribute subset.

Step 11 For each decomposed attribute subset（Sub-attribute）i，perform following steps：

（1）Evolve attribute reduction subset Sub-Rediby the best elitist individual of each decomposed subpopulation.

（2）Optimize each subcomponent gjwith subpopulation by QPSO for a predefined number of FEs.

（3）Choose best attribute reduction subset Rbesti（Rbesti⊆Sub-Redi）in each decomposed attribute subset，respectively.

（4）Compare fitness of Rbesti.

Step 12 Evaluate each decomposed subpopulation of attribute reduction.

Step 13 Collaborate to form complete solution and achieve Redmin＝min｛Rbesti｝.

Step 14 If the halting criterion is satisfied，output the global minimum reduction Redmin，else go to Step 6.

3 EXPERIMENTAL RESULTS AND ANALYSIS

In order to illustrate the effectiveness and efficiency of the proposed METAR algorithm，some experiments on various datasets are carried on，with different numbers of attribute sets.Here all experimental algorithms are encoded in Java and conducted on a PC with Intel（R）Core（TM）2，2.93GHz，CPU Duo and 2GB RAM.Extensive computational studies are carried on to evaluate the performance of the METAR algorithm and other representative algorithms on non-separable optimization functions，UCI datasets and MRI，respectively.

3.1 Non-separable optimization functions

First，the METAR algorithm is evaluated on CEC′2008benchmark functions［14］.Functions f2and f3are completely non-separable in which interaction exists between any two variables.Experiments are conducted on 1000-Dimension of two functions.The maximal FEs is set to 5×106，population size is set to 60.Here the METAR algorithm is compared with three representative cooperative co-evolutionary algorithms， namely DECCG［9］，MLCC［10］and DECCD［12］，which are often used for the decomposition of variable interdependencies.The experimental results in Fig.3 illustrate the evolutionary curves of best fitness found by four algorithms，averaged for 50runs.In order to gain a better understanding of how different algorithms converge，the enlarged figures of the late evolutionary curves are presented more clearly.

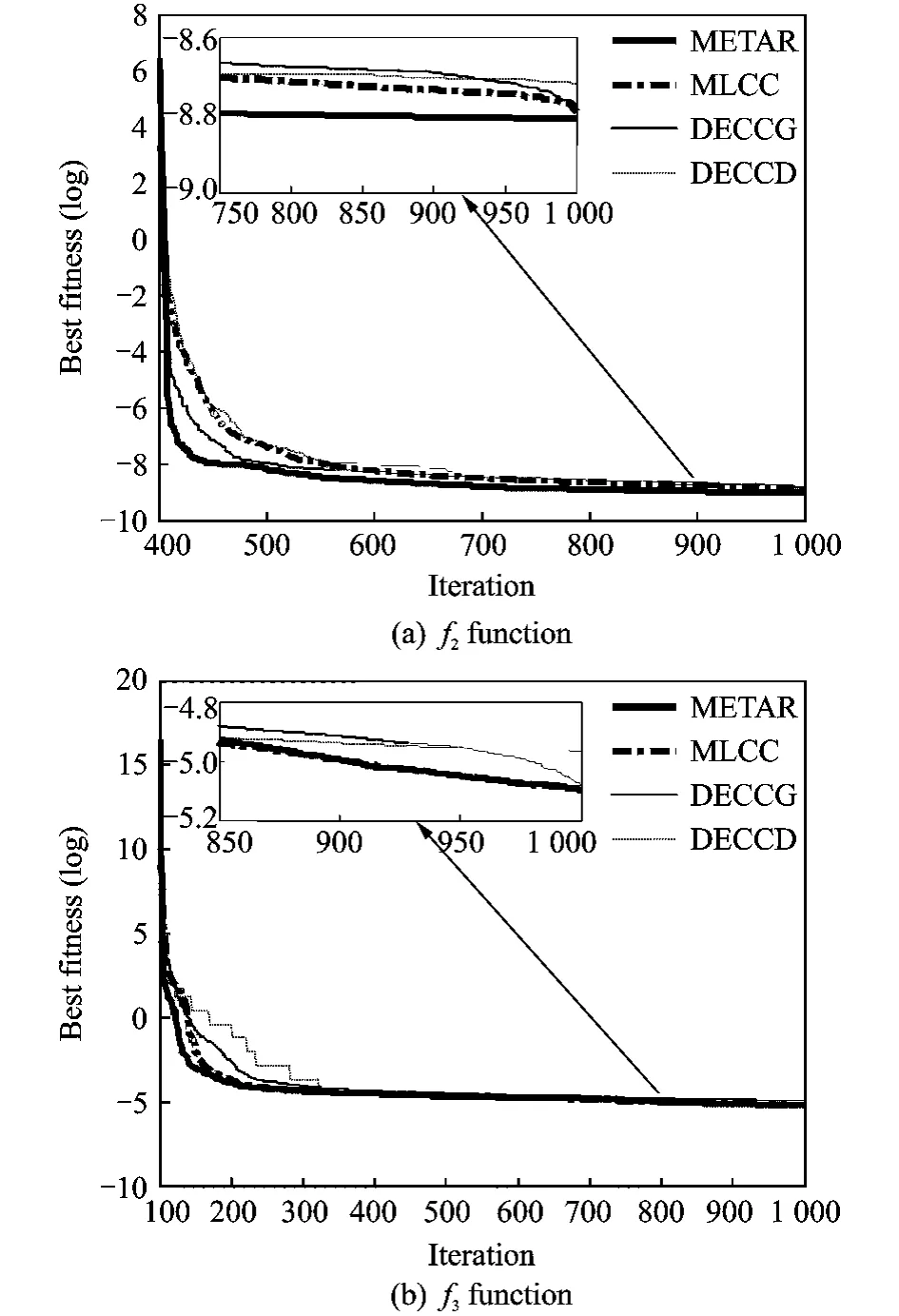
Fig.3 Evolutionary process of mean best values for f2 and f3functions

By comparing the evolutionary curves，it can be seen that the MATAR algorithm is much more effective than other three algorithms in discovering and exploiting the interacting structures inherent for two non-separable functions f2and f3although no prior knowledge is available.It can capture the interacting attribute decision variables in order to group them together in one subpopulation，so it can help to produce the reasonable decompositions.The subpopulation contains more elitists which enhance the global optimization performance.The MATAR algorithm achieves the significantly faster convergence and better scalability for non-separable functions by the model of multilevel evolutionary tree with self-adaptive subpopulations.

3.2 UCI datasets

To further evaluate the effectiveness of the MATAR algorithm for attribute reduction，experiments on five selected UCI datasets［15］are performed.Here average running time and accuracy results of the MATAR algorithm are compared against three representative attribute reduction algorithms based on the evolutionary strategy，i.e.GAAR［5］，ACOAR［6］，and PSOAR［7］.The aver-age results over 50independent runs are summarized in Tables 1－2.The best mean values among four algorithms are marked in bold face.

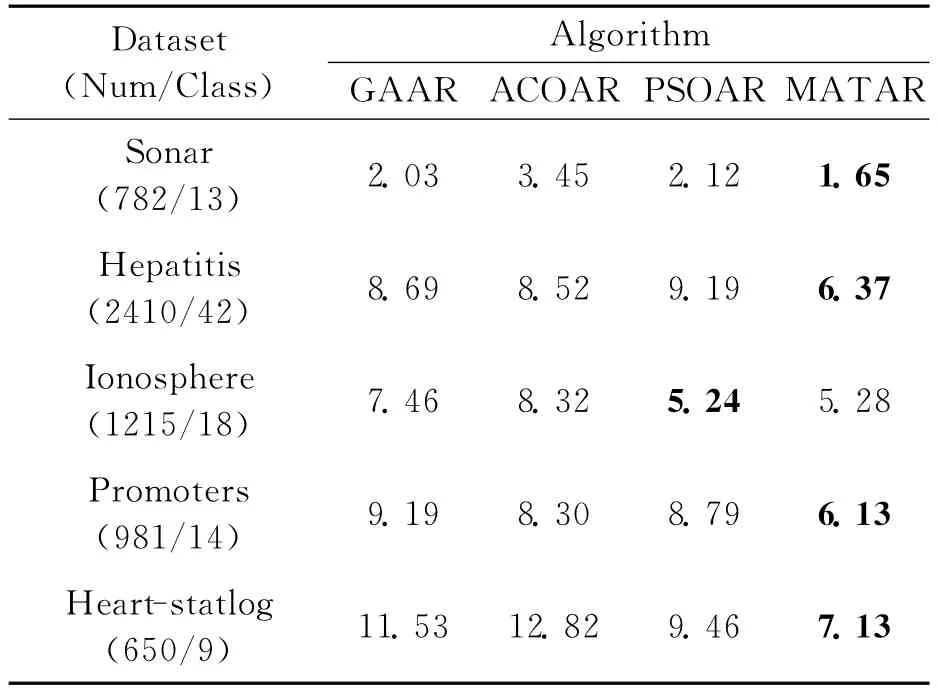
Table 1 Average run time of minimum attribute reduction s

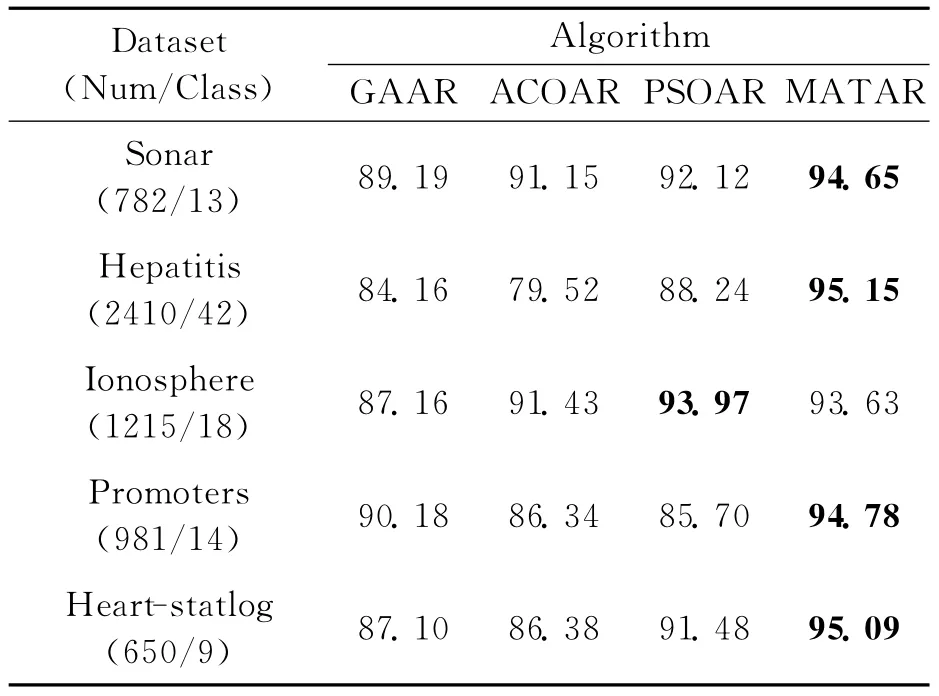
Table 2 Average accuracy of minimum attribute reduction%

It is clear from the two tables that perform-ance of MATAR is significantly better than each of GAAR，ACOAR and PSOAR on all other datasets except of Ionosphere datasets，in which performance of MATAR is also nearly close to the best result.Since the run time of each algorithm is mainly determined by calculating dependency degree，the number of solution constructions is suitable as a main quantity to evaluate the speed of these algorithms.The MATAR algorithm can construct fewer solutions than three compared algorithms and successfully find the optimal reduction set on these datasets.Therefore it can rapidly get the higher accuracy of minimum attribute reduction in the limited time.

3.3 Magnetic resonance image（MRI）

As we all know a major difficulty in the segmentation of MRI is the intensity inhomogeneity due to the radio-frequency coils or acquisition sequences.In the following experiment，the reduction and segmentation performance of MATAR for MRI are evaluated with Gaussian noise level 5%and intensity non-uniformity（INU）30%，in separately 100times.Each size of these images is 256pixel×256pixel，and slice thickness is 1mm.The segmentation results are shown in Fig.4.Fig.4（a）is the original image，and Figs.4（b－f）are the results using GAAR［5］，ACOAR［6］，PSOAR［7］，SFLAAR，and MATAR，respectively.Here SFLAAR is the coding algorithm in which SFLA is applied to the attribute reduction.Note that GAAR，ACOAR and PSOAR are much less fragmented than other algorithms and have somewhat the disadvantage of blurring of some details.Both MATAR and SFLAAR can achieve satisfactory segmentation results for MRI with obvious intensity inhomogeneity，but compared with the result obtained by SFLAAR，the result of MATAR is more accurate，as shown in Fig.4（f）.

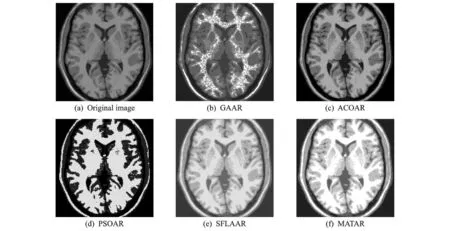
Fig.4 Comparison of segmentation results on MRI corrupted by 5%Gaussian noise and 30%INU

To demonstrate the advantage of MATAR for the segmentation of MRI clearly，Table 3 gives the average time and segmentation accuracy（SA）of five algorithms in detail when the real brain MRI with the same INU 30%corrupted by 5%and 8%Gaussian noise，respectively.Here SA is defined as the sum of the total number of pixels divided by the sum of number of correctly classified pixels.

Table 3 Average time and SA on MRI

It can be observed from Fig.4and Table 3 that the MATAR algorithm can be considered as a more efficient algorithm to be applied to the segmentation of complex medical MRI so as to maintain the better global minimum attribute reduction.Although MRI is corrupted by different Gaussian noises，the MATAR algorithm can achieve higher segmentation accuracy and speed with the more obvious advantages than the other four algorithms.Therefore there are overwhelming evidences to support more excellent feasibility and effectiveness of the proposed MATAR algorithm for minimum attribute reduction，especially for interacting attribute decision variables.

4 CONCLUSION

Aiming at the difficulty in the variable interdependencies and the premature convergence in traditional EA used for minimum attribute reduction，an efficient algorithm，MATAR，is proposed based on multilevel evolutionary tree with self-adaptive co-populations.A model with hierarchical self-adaptive evolutionary tree model is designed to divide attribute sets into subsets with the self-adaptive mechanism according to their historical performance record.It can capture the interacting attribute decision variables so as to group them together in one subpopulation.The experimental results demonstrate the proposed MATAR algorithm remarkably outperforms some existing representative algorithms.Therefore it is a much more effective and robust algorithm for interacting attribute reduction.

The future work will focus on the more indepth theoretically analysis of the MATAR algorithm and its relation to incomplete attribute reduction characteristics of 3DMRI segmentation by better self-adaptively coping with local and global intensity inhomogeneity simultaneously.

［1］ Pawlak Z.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11（5）：341-356.

［2］ Yao Y Y，Zhao Y.Attribute reduction in decisiontheoretic rough set models ［J］.Information Sciences，2008，178（17）：3356-3373.

［3］ Qian Y H，Liang J Y，Pedrycz W，et al.Positive approximation：An accelerator for attribute reduction in rough set theory ［J］.Artificial Intelligence，2010，174（9／10）：597-618.

［4］ Wong S K M，Ziarko W.On optimal decision rules in decision tables［J］.Bulletin of Polish Academy of Science，1985，33（11）：693-696.

［5］ Slezak D，Wroblewski J.Order based genetic algorithms for the search of approximate entropy reducts［C］∥the 9th International Conference on Rough Sets，Fuzzy Sets，Data Mining and Granular Computing.Chongqing，China：［s.n.］，2003：308-311.

［6］ Ke L J，Feng Z R，Ren Z G.An efficient ant colony optimization approach to attribute reduction in rough set theory［J］.Pattern Recognition Letters，2008，29（9）：1351-1357.

［7］ Ye D Y，Chen Z J，Liao J K.A new algorithm for minimum attribute reduction based on binary particle swarm optimization with vaccination［C］∥PAKDD 2007.Nanjing，China：［s.n.］，2007：1029-1036.

［8］ Potter M A，De Jong K A.A cooperative coevolutionary approach to function optimization［C］∥Proceeding of the Parallel Problem Solving from Nature-PPSN III，Int′l Conf on Evolutionary Computation.Berlin：Springer-Verlag，1994：249-257.

［9］ Yang Z，Tang K，Yao X.Differential evolution for high-dimensional function optimization［C］∥Proceeding of the 2007Congress on Evolutionary Computation.Singapore：IEEE，2007：3523-3530.

［10］Yang Z，Tang K，Yao X.Multilevel cooperative coevolution for large scale optimization［C］∥Proceeding of IEEE World Congress on Computational Intelligence.Hong Kong，China：IEEE，2008：1663-1670.

［11］Ray T，Yao X.A cooperative coevolutionary algorithm with correlation based adaptive variable parti-tioning［C］∥2009IEEE Congress on Evolutionary Computation （CEC 2009）.Trondhelm，Norway：IEEE，2009：983-989.

［12］Omidvar M N，Li X D，Yao X.Cooperative co-evolution with delta grouping for large scale non-separable function optimization［C］∥2010IEEE World Congress on Computational Intelligence.Barcelona，Spain：IEEE，2010：1762-1769.

［13］Omkar S N，Khandelwal R，Ananth T V S.Quantum behaved particle swarm optimization（QPSO）for multi-objective design optimization of composite structures［J］.Expert Systems with Applications，2009，36（8）：11312-11322.

［14］Tang K，Li X，Suganthan P N，et al.Benchmark functions for the CEC′2008special session and competition on large-scale global optimization［R］.Hefei，China：Nature Inspired Computation and Applications Laboratory，2007.

［15］Asuncion A，Newman D J.UCI repository of machine learning databases［EB／OL］.http：∥www.ics.uci.edu／～mlearn／mlrepository，2007-06／2011-10-6.