基于混沌系统的水下目标辐射噪声线谱检测

石 敏，徐 袭

(1.水声对抗技术重点实验室，广东 湛江，524022;2.中国人民解放军91388 部队，广东 湛江，524022)

0 引 言

水下目标辐射噪声中的线谱成分含有丰富的信息，对其进行准确检测在水下目标的被动识别、探测和跟踪中具有十分重要的意义。

通常情况下，辐射噪声线谱具有频率低(100 Hz 以下)和强宽带背景噪声属于弱信号的特点，采用频谱分析的方法很难检测到。近些年来，基于混沌理论的微弱线谱检测方法发展较快，已成为当代非线性研究领域的一个热门问题［1-4］。其主要利用了混沌系统具有对噪声及与混沌系统内置信号频差较大的信号具有免疫力，而对与混沌系统内置信号频率相同的信号敏感的特点。

在混沌系统微弱信号检测中，一般采用基于Lyapunov 指数［5-6］或Melnikov 函数［7］判据的方法区分系统状态，从而对微弱线谱的有无进行检测。而这些判据计算较复杂，本文提出采用相轨迹内径的方法确定混沌系统状态及内置信号阈值。仿真结果表明内径判据更直观简单，适合于水下目标辐射噪声中微弱线谱的检测。

1 基于混沌理论的微弱线谱检测

在微弱线谱检测中应用较多的是Holmes 型的duffing 振子，其方程形式为:

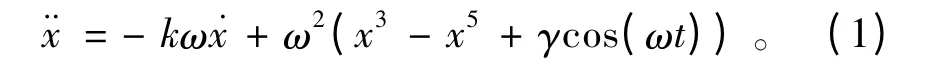
式中:ω 和γ 分别为混沌系统内置信号角频率和幅度;k 为阻尼系数，一般取为0.5;t 为采样时间;˙x 和¨x 分别为x 的一阶和二阶微分; (x3-x5)为非线性项。该振子适合于任意频率的微弱线谱检测。

随着幅度γ 的逐渐增大，系统将历经同宿轨迹、分叉轨迹、混沌状态、混沌临界状态和大尺度周期状态。当γ 到达临界值γd时，系统将到达混沌临界状态。此时，在系统中注入含有噪声且与内置信号频率相同的正弦信号时，系统将由混沌状态进入到大尺度周期状态;而在系统中注入纯噪声时，系统仍保持混沌状态，只是在原运动轨迹上出现毛刺。因此根据混沌临界状态下，系统是否进入大尺度周期状态可对水下目标辐射噪声微弱线谱进行检测。

在混沌微弱信号检测中，一般根据Lyapunov指数或Melnikov 函数判据的方法确定混沌系统所处的状态。而这些方法计算较复杂，本文提出采用内径判据的方法确定混沌系统状态及临界阈值。

1.1 临界阈值γd的确定

定义相轨迹的内径r 为:

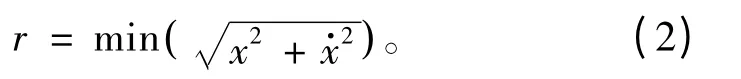
即相轨迹中所有半径的最小值为内径。

r 随着γ 的变化而变化，当系统由混沌状态跃变为大尺度周期状态时，内径r 将发生跃变，据此可确定临界阈值γd。

以内置信号频率ω=2π 为例，取50 个周期长的信号，γ 取值范围为0.1 ～2，取样步长为0.01，其内径r 与内置信号幅度γ 之间的关系曲线如图1(a)所示。

图1(a)中，内径r 在γ=0.8 处发生跃变，因此γd=0.79。图1(b)和图1(c)分别给出了γ=0.79 和γ=0.8 时对应的系统相轨迹图。

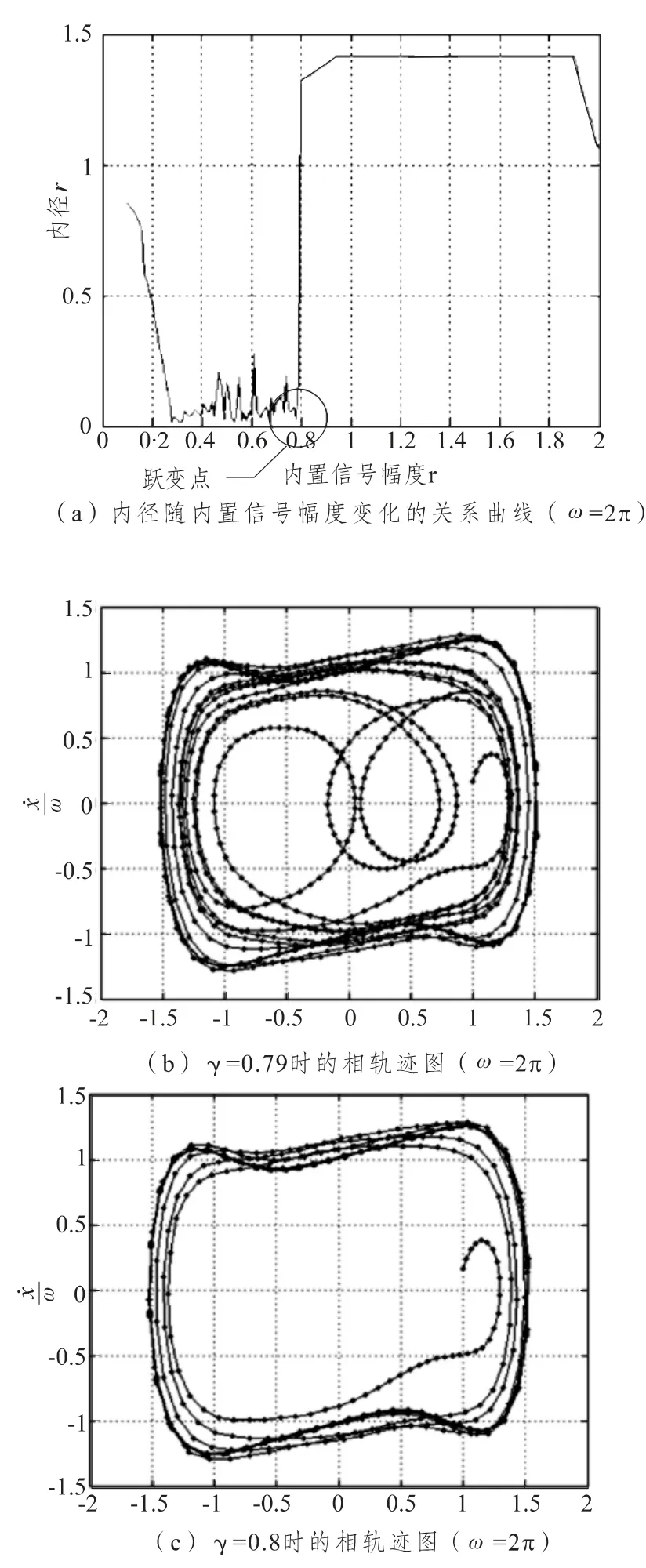
图1 临界阈值γd的确定(ω=2π)Fig.1 Determining limited value γdof critical state (ω=2π)

为消除不同ω 对系统相轨迹图的影响，对˙x 进行了归一化处理，即相轨迹图中以纵坐标˙x /ω 代替˙x 。图1 结果证实了基于内径确定γd方法的准确性。若要确定更精确的γd值，可将γ 在0.79 ～0.8 之间的取样步长减小，根据r 与γ 之间的关系曲线确定γd的精确值。

表1 给出了根据本文方法确定的不同ω 值对应的γd值。

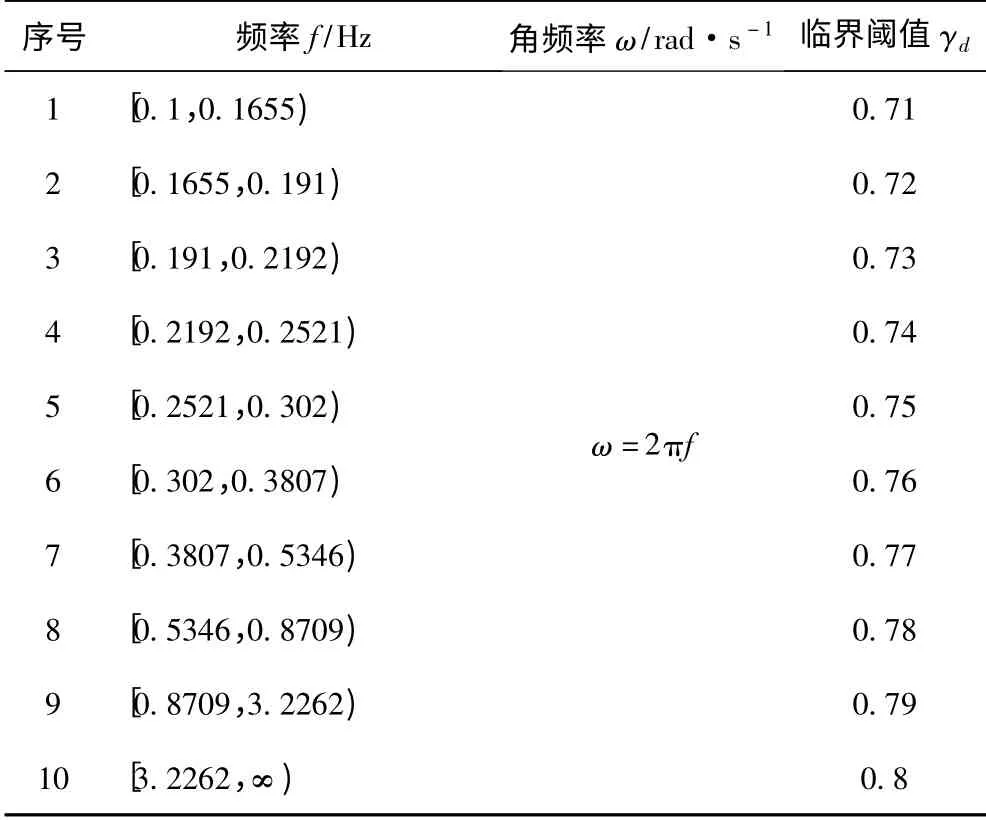
表1 不同ω 对应的γd值Tab.1 The value of γdcorresponding to various ω

1.2 微弱线谱检测

确定混沌临界阈值后，使混沌系统式(1)处于混沌状态，在系统中注入待测信号s(t)，此时系统方程为:

式(3)中，待测信号s(t)为:

或

式(4)和式(5)中的n(t)为高斯白噪声，式(5)中的ωx和a 分别为s(t)中所含信号的角频率和幅度。

图2(a)给出了当s(t)为式(4)的形式，即s(t)为纯噪声时，式(3)对应的相轨迹图。

由图2(a)可知，系统内置角频率为ω=2π 时，在处于临界状态的系统中注入纯噪声，系统仍保持混沌状态，且内径为0.015 4。图2(b)给出了式(3)中s(t)=n(t)时，系统相轨迹内径随内置信号频率变化的曲线(由于舰船辐射噪声一般低于100 Hz，因此本文中的频率只考虑1 ～100 Hz)。可见纯噪声情况下，其内径均很小。

当s(t)为式(5)时，即s(t)中含有频率为ωx=2π 的单频信号且含有信噪比SNR=-20dB 的高斯白噪声时，式(3)对应的相轨迹图如图3(a)所示。

图2 纯噪声测试结果Fig.2 The testing result of pure noise

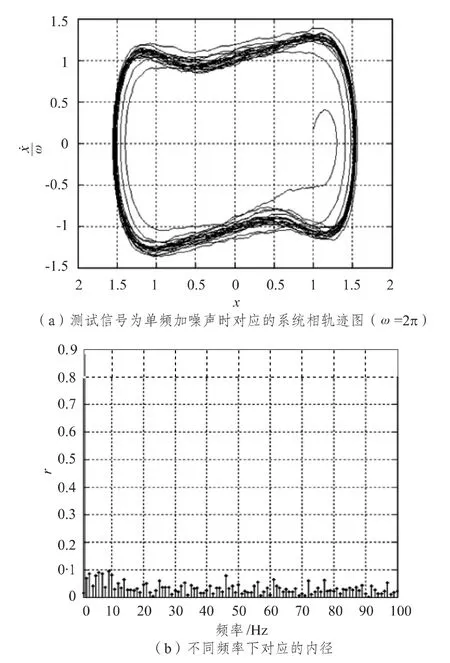
图3 单频加噪声测试结果Fig.3 Test results of single frequency signal with noise

由图3(a)可见，当系统处于临界状态，在系统中注入与内置信号频率相同的微弱信号时，系统将进入大尺度周期状态。图3(b)给出了式(3)中s(t)为式(5)形式时，系统相轨迹内径随内置信号频率变化的曲线。可见对于微弱线谱信号，当系统内置频率与待测信号所含频率相同时，其相轨迹的内径将很大。据此可实现微弱线谱检测。

2 仿真分析

信号采样率为2 000 Hz，信号长度取为10 s，信号中含有4 Hz，8 Hz，12 Hz 的正弦信号，信噪比为SNR=-20 dB。首先对信号采用2 ～150 Hz 的滤波器进行滤波。图4(a)给出了直接利用FFT 频率分析的结果，图4(b)给出了采用混沌方法得到的100 Hz 以下频率的频率-内径图。

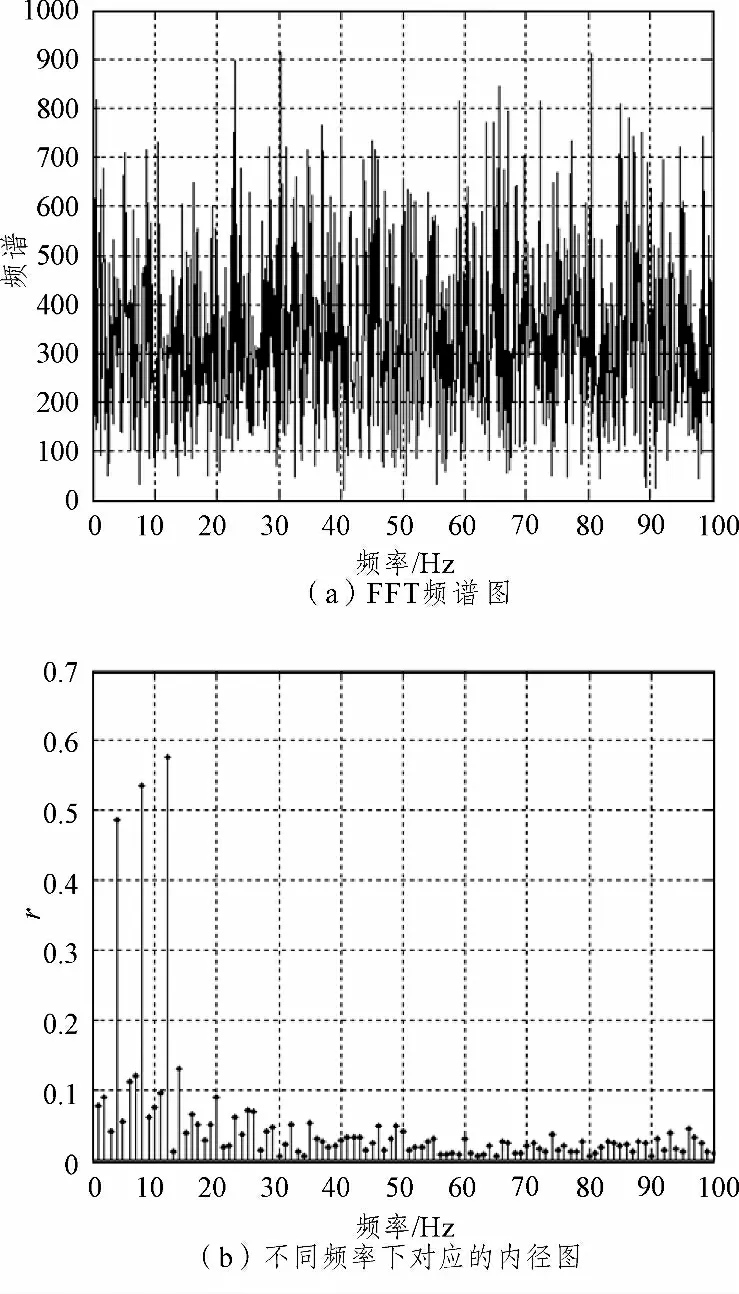
图4 仿真信号测试结果Fig.4 Test results of emulation signal

由仿真结果可知，直接FFT 频谱分析法中，信号频谱淹没在噪声频谱中，而利用混沌检测方法中的频率-内径分布图则能检测到信号频率。

3 结 语

本文采用混沌理论进行水下目标辐射噪声微弱线谱检测，其主要创新点在于:

1)在混沌理论微弱线谱检测中，提出了利用相轨迹内径确定混沌临界状态阈值及区分混沌与大周期状态的方法，较之利用其他方法更简单直观。

2)采用频率-内径分布图可实现低信噪比下线谱信号的检测。

在本文混沌弱信号检测方法中，只考虑100 Hz以下的频率成分，且频率分辨率为1 Hz。若要实现更精确的频率检测，则需要计算更多内置信号频率下对应的内径，将增大计算量。将混沌理论用于实际的信号检测还需作进一步的研究。

［1］GAO X，YU J B.Chaos in the fractional order periodically forced complex duffing′ s oscillators［J］.Chaos Soliton Fract，2005，24:1097-1104.

［2］李月，杨宝俊，袁野，等.混沌振子检测系统的弱有效地震信号检测能力［J］.科学通报，2006，51(14):1710-1716.

［3］楼天良.基于混沌理论的微弱线谱信号检测研究［J］.舰船科学技术，2009，31(1):96-99.

［4］郑思仪，郭红霞，李亚安，等.一种用duffing 振子检测舰船辐射噪声线谱的新方法［J］.科学通报，2007，52(3):258-263.

［5］陈伟根，张嵩，杜林，等.基于互相关与混沌检测相结合的光声信号检测方法［J］.电力自动化设备，2008，28(3):22-26.

CHEN Wei-gen，ZHANG Song，DU Lin，et al.Photoacoustic signal measuring based on cross-correlation analysis and chaotic detection［J］.Electric Power Automation Equipment，2008，28(3):22-26.

［6］陈伟根，云玉新，杜林，等.基于互相关和李雅普诺夫指数的微弱正弦信号混沌检测［J］.电子系统自动化，2008，32(18):44-48.

［7］侯楚林，熊萍，王德石.基于互相关与混沌理论相结合的水下目标信号检测［J］.鱼雷技术，2006，14(5):17-19.

HOU Chu-lin，XIONG Ping，WANG De-shi.Detection of underwater target signals by combining cross-correlation with chaos theroy［J］.Torpedo Technology，2006，14(5):17-19.