高阶矩有效微地震事件拾取处理方法

宋维琪，喻智超，杨勤勇，姜宇东，郭全仕

（1.中国石油大学（华东）地球科学与技术学院，山东青岛266580；2.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103）

微地震信号自动拾取或地震震相识别方法有能量比法、赤池弘次信息准则（AIC）法、神经网络法、分形分维法、极化分析法以及卡尔曼估计法等。其中，能量比法是最为快捷、应用最为广泛的一种自动拾取方法［1－3］。为了更好地适用于微地震事件的拾取，一般设计长时窗（LTA，Long Time Average）与短时窗（STA，Short Time Average），计算出地震数据的绝对值、能量或包络面，作为识别有效事件的特征函数，通过分析长／短时窗特征函数的比值是否大于预先设定的门限来识别有效地震信号。目前这种长／短时窗比法已成为各个微地震监测公司最为常用的方法。不过这种方法亦有其缺陷：①受短时窗的影响不能准确拾取初至；②难以在高振幅噪声中分辨出有效微地震信号。Chen［4］对长／短时窗能量比法进行了改进，设计了多时窗算法，在一定程度上克服了上述缺点。偏振分析也是区分信号与噪声的一个重要手段，利用地震信号因线性偏振而偏振度（极化度）高、噪声偏振度低的特点分辨地震信号［5－7］。Anant等认为，对地震信号进行多尺度小波分解后，原信号的偏振特性仍会体现在各个尺度上，由此提出对小波变换主成分进行偏振分析的方法。周彦文等［9－11］讨论了初至自动识别方法，将该方法的检测结果与AIC方法的检测结果进行对比后认为，在低信噪比条件下，时频域偏振性检测结果的精度更高。刘希强等［12］对这种方法进行了进一步探讨，提出在各个小波尺度上求取偏振度，将各个尺度上的信息相结合作为识别因子，提高了算法的抗噪声能力［13］。

尽管微地震有效事件的拾取方法很多，但是考虑到实际应用情况和海量地震数据必须快速有效地进行拾取计算［14－16］，目前主要采用能量比方法。鉴于能量比方法对于低信噪比资料的拾取效果不理想［17］，我们研究提出了基于高阶矩分析的有效微地震事件拾取方法，较好地解决了低信噪比情况下有效微地震事件的拾取问题。

1 高阶矩方法原理

1.1 随机过程的高阶矩

设｛x（t）｝为k阶平稳随机过程，则该过程的k阶矩定义为［18－19］

式中：mom是指矩量方法。根据这一定义，随机过程｛x（t）｝的一阶矩为

式中：E｛x（t）｝为x（t）的均值。二阶矩为

式中：r｛x（τ1）｝为x（t）的自相关函数。三阶矩为

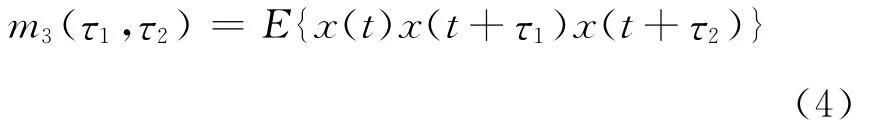
四阶矩为

1.2 长／短时窗能量比法

长／短时窗能量比法是一种基于时域的自动识别方法。在一定信噪比条件下，地震记录的能量在有效波初至出现前、后会有比较明显的差异，长／短时窗能量比法即根据这种差异识别有效信号。在方法实现过程中，主要考虑窗口、触发门限等因素的影响［20－22］。

对于一道三分量记录（X（t），Y（t），Z（t）），可以用来求能量的组合有

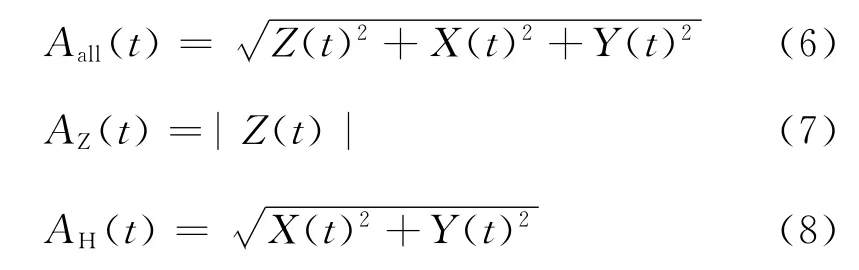
式中：Z（t）为垂直分量；X（t），Y（t）为水平分量；Aall（t）为三分量总能量和；AZ（t）为垂直分量能量；AH（t）为水平分量能量。

当实际微地震资料信噪比较高时，长／短时窗能量比法效果较好；但是当信噪比较低时，该方法的应用效果不理想。

1.3 长／短时窗能量比的高阶中心矩方法

随机变量的高阶中心矩定义为

通过实际资料试算分析，四阶中心矩效果最好。

其中，EC（t）为t时刻的能量，为（6）式至（8）式中某一种情况；EB（t）为前时窗（Before Time Average），范围为t1～t0；EA（t）为后时窗（After Time Average），范围在t0～t2；ED（t）指延迟时窗能量的平均值（Delay Time Average），起始于t3，终止于t4。根据这些能量值，可以构造出3种识别有效微地震信号的准则。

研究发现，微地震资料的能量和频谱成分随着时空变化而变化［23－24］。对于不同的事件或同一事件的不同分量，其能量的变化也不同，利用固定的门槛值会漏拾某个分量。通过对数据取对数，可以改善其能量水平的差异。

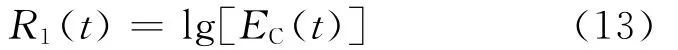
R1（t）用来判断在t时刻是否出现强能量信号。R2（t）用来区分强振幅、短延续时间噪声与强振幅、长延续时间的有效信号，利用了前时窗EB（t）足够大、窗口长度是噪声延续长度的多倍时R2（t）受噪声影响不大的特点。在噪声延续时间比较长的情况下，R2（t）失去效果，这时可以将前时窗EB（t）向后推迟一段时间得到延迟时窗EA（t），根据这个时窗内的平均能量值求得R3（t），通过判断R3（t）是否超过门限值来去除长延续时间噪声的影响。

因此，计算长时窗（LTA）与短时窗（STA）信号在t0时刻的能量比值R（t0），即

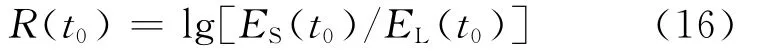
当R（t0）超过设定阈值的时候，可以判断为有效信号。其中，

窗口大小和长、短两个窗口相对大小对微地震事件的拾取有较大的影响。不同微地震事件记录，其主频不同，对不同主频的微地震事件采用相同窗口是不合适的。因此，在算法设计时，应把固定窗口改进为自适应变化窗口。

1.4 相关方法滤波

通过中心矩长／短时窗能量比计算再取对数后，有效事件信号得到了明显加强。但是如果只有某几道信号得到加强，还不足以判断事件是否为有效事件。因此，对上述计算结果再进行以下分析：首先进行相关滤波，然后通过相关方法计算各道的时移量（即视速度大小）来判断是否为有效事件。

2 效果分析

分别应用二阶矩、三阶矩和四阶矩方法对某工区1127和1149两个事件记录资料进行了分析，同时和常规的长／短时窗能量比方法进行了对比，结果如图1和图2所示。分析图1和图2可知，应用矩量方法特别是四阶矩方法处理后，有效信号的差异更加明显；四阶矩方法除了使有效信号差异明显外，对噪声还有相当程度的压制作用。

图1 1127事件处理结果

图2 1149事件处理结果

3 结束语

基于高阶矩分析的有效微地震事件拾取方法能较好地解决低信噪比情况下有效微地震事件拾取效果不理想的问题。

1）通过中心矩长／短时窗比计算再取对数后，有效事件信号得到了明显加强。

2）窗口大小和长、短两个窗口相对大小直接影响有效事件的漏拾率。将固定窗口改进为自适应变化窗口，能使微地震资料的比值效果明显改善。

3）采用相关方法对计算结果进行相关滤波，再通过相关方法计算各道的时移量，能使有效事件清楚，更容易拾取。

［1］Maxwell S C，Urbancic T I.The role of passive microseismic monitoring in the instrumented oil field［J］.The Leading Edge，2001，20（6）：636－639

［2］Warpinski N R，Branagan P T，Peterson R E，et al.Mapping hydraulic fracture growth and geometry using microseismic events detected by a wireline retrievable accelerometer array［R］.Calgary，Alberta，Canada：SPE Gas Technology Symposium，1998

［3］Moriya H，Niitsuma H.Precise detection of a P－wave in low S／N signal by using time－frequency representations of a triaxial hodogram［J］.Geophysics，1996，61（5）：1453－1466

［4］Chen Z L.A multi－window algorithm for automatic picking of microseismic event on 3－C data［J］.Expanded Abstracts of 75thAnnual Internat SEG Mtg，2005，1288－1291

［5］Rutledge J T，Phillips W S，Mayerhofer M J.Faulting induced by forced fluid injection and fluid flow forced by faulting：an interpretation of hydraulicfracture microseismicity，Carthage Cotton Valley Gas Field［J］.Bulletin of the Seismological Society of America，2004，94（5）：1817－1830

［6］Maxwell S C，Rutledge J，Jones R，et al.Petroleum reservoir characterization using downhole microseismic monitoring［J］.Geophysics，2010，75（5）：129－137

［7］陆菜平，窦林名，吴兴荣，等.岩体微震监测的频谱分析与信号识别［J］.岩土工程学报，2005，27（7）：772－775 Lu C P，Dou L M，Wu X R，et al.Spectrum analysis and signal recognition of microseismic monitoring of rock mass［J］.Chinese Journal of Geotechnical Engineering，2005，27（7）：772－775

［8］Anant K S，Dowla F U.Wavelet transform methods for phase identification in three－component seismograms［J］.Bulletin of the Seimological Society of A－merica，1997，87（6）：1598－1612

［9］周彦文，刘希强.初至震相自动识别方法研究与发展趋势［J］.华北地震科学，2007，25（4）：18－22 Zhou Y W，Liu X Q.First arrival phase automatic recognition research and development trend of method［J］.North China Earthquake Science，2007，25（4）：18－22

［10］Sleeman R，van Eck T.Robust automatic P－phase picking：an on－line implementation in the analysis of broadband seismogram recording［J］.Physics of the Earth and Planetary Interiors，1999，113（1－4）：265－275

［11］Zhang H J，Thruber C，Rowe C.Automatic P－wave arrival detection and picking with multiscale wavelet analysis for single－component recording［J］.Bulletin of the Seimological Society of America，2003，95（5）：1904－1912

［12］刘希强，周蕙兰，沈萍，等.用于三分向记录震相识别的小波变换方法［J］.地震学报，2000，22（2）：125－131 Liu X Q，Zhou H L，Shen P，et al.For three points to the recording phase identification and wavelet transform method［J］.Journal of Earthquake，2000，22（2）：125－131

［13］Wang J，Teng T L.Artifical neural network－based seismic detector［J］.Bulletin of the Seimological Society of America，1995，85（1）：308－309

［14］Baziw E，Jones I W.Application of Kalman filtering techniques for microseismic event detection［J］.Pure and Applied Geophysics，2002，159（1－3）：449－471

［15］Baziw E，Nedilko B，Jones I W.Microseismic event detection Kalman filter：derivation of the noise covariance matrix and automated first break determination for accurate source location estimation［J］.Pure and Applied Geophysics，2004，161（2）：303－329

［16］Gajewski D，Anikiev D，Tessmer E，et al.Localization of seismic events by diffraction stacking［J］.Expanded Abstracts of 77thAnnual Internat SEG Mtg，2007，1287－1291

［17］宋维琪，吕世超.基于小波分解与Akaike信息准则的微地震初至拾取方法［J］.石油物探，2011，50（1）：14－21 Song W Q，Lv S C.Wavelet decomposition and the Akaike information criterion of micro seismic firstbreak picking method based on［J］.Geophysical Prospecting for Petroleum，2011，50（1）：14－21

［18］宋维琪，曹自强，刘仕友.多尺度四阶累积量相关分析方法及其应用［J］.石油物探，2006，45（6）：607－610 Song W Q，Cao Z Q，Liu S Y.Multiscale four order cumulant correlation analysis method and its application［J］.Geophysical Prospecting for Petroleum，2006，45（6）：607－610

［19］Liang G H，Cai X P，Li Q Y.Using high－order cumulants to extrapolate spatially variant seismic wavelets［J］.Geophysics，2002，67（6）：1869－1876

［20］孙政，胡修林，涂平洲.高阶统计量方法及应用研究［J］.计算机与数字工程，2003，31（6）：59－62 Sun Z，Hu X L，Tu P Z.Study on methods and applications of higher－order statistics［J］.Computer and Digital Engineering，2003，31（6）：59－62

［21］杜宁平，史军，朱红涛.高阶统计量分析在有期预测中的应用［J］.海洋地质动态，2004，20（8）：27－29 Du N P，Shi J，Zhu H T.Higher order statistics analysis in prediction of the application period［J］.Marine Geological Dynamic，2004，20（8）：27－29

［22］杨晨明.高阶统计量在检测中的应用［J］.自动化学报，1994，20（6）：288－294 Yang C M.Application of high－order statistics in the detection of［J］.Journal of Automation，1994，20（6）：288－294

［23］Velis D R，Ulrych T J.Simulated annealing wavelet estimation via fourth－order cumulant matching［J］.Geophysics，1996，61（6）：1939－1948

［24］石殿祥，李岩，殷福亮，等.基于高阶累积量的非最小相位地震子波提取［J］.石油地球物理勘探，1999，34（5）：491－499 Shi D X，Li Y，Yin F L，et al.Extraction of non minimum phase seismic wavelet based on higher－order cumulants［J］.Oil Geophysical Prospecting，1999，34（5）：491－499