炸药震源定向激发方式数值模拟及效果对比

蔡纪琰，孙成禹，项龙云，张晓钊

（中国石油大学（华东）地球科学与技术学院，山东青岛266580）

随着勘探开发需求的提高和地震勘探技术的发展，对地震探测分辨率提出了更高的要求。震源激发方式是影响地震记录品质的主要因素之一。激发震源所产生的子波应满足以下条件［1］：较宽的频带宽度，即地震波应包含足够的高频和低频成分；较高的主频，即能够满足地震勘探分辨率的需要；足够的地震波能量，保证反射波的能量能被仪器接收到且有较高的信噪比。

通常情况下，要增大勘探深度就必须增加药量；但药量的增加又会使地震波的主频降低，从而降低了勘探分辨率。因此，既要增大地震波向下传播的能量又要使地震波具有较高的主频成为目前震源激发研究的主要方向。

目前对于震源激发方式的研究主要集中在4方面：①时延爆炸震源激发［1－2］；②长药柱激发［3］；③点源组合激发［4－5］；④相控 震源激 发［4，6－8］。其中相控震源主要用于可控震源，对于陆上常用的炸药震源这方面的研究还仅处于理论方面。

我们利用波动方程有限差分正演技术［9－10］，对上述4种震源组合的机理进行了数值模拟。根据模拟结果，对上述几种激发方式进行定量分析，研究了不同激发方式的波场特征，并将这些激发方式与点震源激发方式的激发效果进行对比，分析总结出不同激发方式的优缺点。最后，结合生产实际给出了不同激发方式在应用过程中应注意的问题及其适用条件。

1 炸药震源定向激发原理及数值模拟方法

1.1 细长药柱震源

细长药柱震源激发基本原理就是顶部起爆依次传播到底部。由于炸药的爆速一般大于激发的地震波速度，所以炸药内部爆轰波传播时间与介质中地震波传播时间有一个时间差，如果把细长药柱震源看成一系列点震源的组合，就可以根据爆速、地震波传播速度以及分节的药柱长度求出这个时间差，然后用垂向组合点震源通过时间延迟来模拟柱状震源。

根据波动理论的推导［11］，柱状爆炸情况下的声波方程表达式为

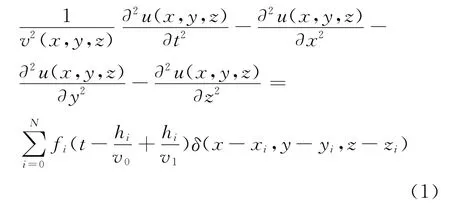
式中：fi（x，y，z）为外加应力，即炸药起爆对介质质点的作用力；N为组合节数；v1为炸药爆速；hi为药柱上各点到药柱顶端的距离；v0为爆炸点介质的波速。

1.2 时延爆炸震源

时延爆炸震源是从柱状震源发展演化出来的一种震源，激发基本原理与细长药柱震源的相差不多，其核心手段是控制不同段炸药的激发延迟时间来抵消爆速与地震波传播速度的差异。

根据波动理论的推导过程［11］，延迟爆炸情况下的声波方程表达式为

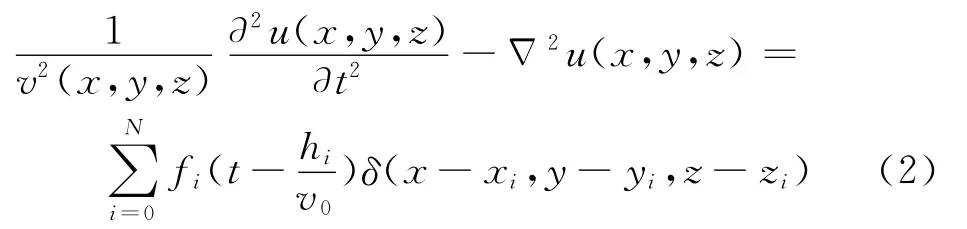
式中：N为延迟级数。与常规激发方式相比，各炸药延迟爆炸的结果是使向下传播的地震波能量达到最大，图1为延迟爆炸方式的波阵面传播示意图。基于图2所示的介质模型，利用公式（2）的波动方程进行正演模拟，得到的波场快照和能量照明如图3所示。可以看出，在药量相同的情况下，向下传播的地震波能量随着延迟级数的增加而增加，而向上传播的能量则减少。从图1还可以看出，随着延迟震源基间距的增加可以使向下传播的能量越来越集中，向上传播的能量越来越少。即通过使用延迟震源可以达到增加向下传播能量的目的。

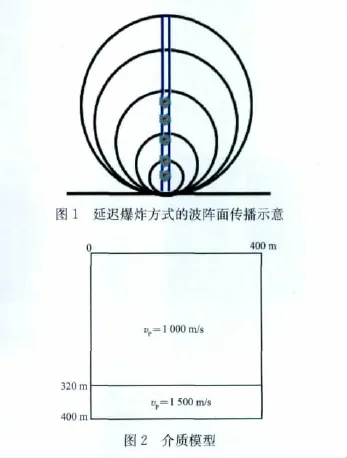
图3 不同延迟级数时延震源激发模拟的能量照明和波场快照

1.3 相控爆炸震源

相控震源的概念来源于雷达系统的相控阵天线［6－8］，其最大的特点是能使地震波按预定方向激发，目前主要用于可控震源，所以实际上只考虑了地下半空间地震波的方向性。徐峰等［4］和汪仁富等［5］研究了用于炸药震源的情况，并给出了整个空间的地震波的方向性问题。总波场的归一化场强方向因子为

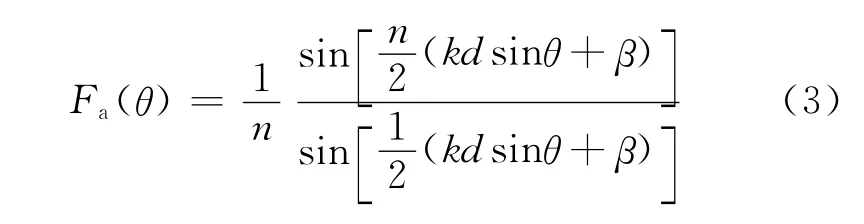
式中：β为相邻震源间的恒定相位差；n为震源个数；k为波数，k＝2π／λ；d为震源间距。当相邻震源间相位差（kdsinθ＋β）不同时，最大能量的指向会发生变化，所以可以通过控制其恒定相位差β来调整最大能量的指向。

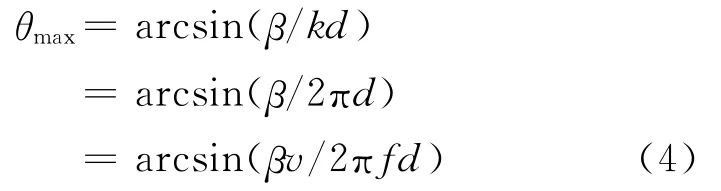
从公式（4）可以看出，当介质速度一定时，最大能量指向只与地震波频率有关。图4为n＝4，d＝5m，v＝1 000m／s，β＝0时，不同频率下的最大能量定向图。

由图4可见，随着频率的增加能量在两个方向上出现了极大值。这不利于定向激发。由推导可得，能量不出现多个极大值的条件为d＜λ／n。由于实际过程中我们更关心的是主能量方向的宽度，一般用最大能量指向为垂直方向时的半功率宽度表示［5］，即

图4 不同频率下相控震源激发模拟的地震波能量方向

从（5）式可以看出，能量随着炮数的增加而集中于某一方向，许多学者根据场强方向因子做出极化图进行讨论，但不很直观，我们使用能量照明图的方法，给出了更直观的指示效果。相控震源的能量定向一般通过调节恒定延迟相位来控制，此延迟相位可以转换为延迟时间或延迟井深。对于炸药震源，为了控制方便通常转换为井深。其井深差与最大能量方向角之间的关系为

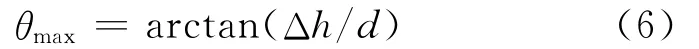
式中：Δh为延迟井深差。以n＝4，d＝8m，λ＝33m为例，利用波动方程正演得到不同井深差条件下不同方向上的能量照明图和波场快照如图5所示，从图5中可以直观地看出能量的定向。在实际工作中，应根据前期地质调查的结果确定勘探范围和地层倾斜角度大小，通过控制激发井深达到控制地震波能量传播方向的目的。

1.4 水平组合震源

水平组合震源是相控震源恒定相位差β＝0时的特例，这里不再做过多介绍。

图5 不同井深差相控震源激发模拟的能量照明和波场快照

2 定向激发方法评判准则及其数值模拟效果对比

2.1 评判准则

2.1.1 定向性的评判准则

公式（5）为相控震源半功率宽度的计算表达式，但由于其假设条件（检波器接收子波的位置为无限远）的限制，使得利用该公式计算出的半功率宽度只能定性而不能定量。为了定量研究炸药震源不同组合能量传播的方向特性，首先引进边际能量密度的概念，并给出地震波束主方向、汇聚带、半功率宽度的确切定义［11］。

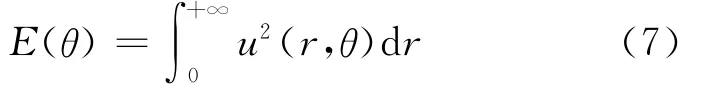
为地震波场沿θ方向的边际能量密度，θ∈［－90°，90°］；将（θ）的自变量值θ＝θmax给出的方向称为地震波束的主方向；E≥0.707Emax的区间［θ1，θ2］称为地震波束的汇聚带；Δθ＝θ2－θ1称为地震波束的宽度。边际能量密度值的大小可以用来定量的衡量沿θ方向的地震波能量的强弱。下面通过一个具体的模型来讨论不同震源激发方式的方向特性。

在波速v＝1 000m／s，网格为500×300的均匀半空间的边界上分别布设延迟、细长、组合、相控4种不同震源组合激发方式进行激发。其中组合与相控震源激发为4炮，组合间距为2个网格点；相控震源激发采用的是井深差激发，相邻震源点间的井深差为1个网格点；延迟震源与细长药柱震源都是采用的4节激发，每个节点的距离为1个网格点。

图6是根据波动理论获得地震波场的时间切片u（r，θ）。从图6可看出，相控震源激发以及组合震源激发时波场振幅值分布不均匀，其值的最大方向如箭头所示；延迟震源隐约可以看出其最大值的方向垂直向下，细长药柱震源已经看不出最大值的方向。

图7是不同震源激发方式的边际能量密度图，从图7中可以直观地看出，相控震源的主波束的能量最大方向大概在26°，汇聚带在0～55°，主波束的宽度为55°，能量密度值在－55°的方向上出现了一个极小值，这是多个震源信号在传播过程中相互干涉叠加的结果；细长药柱震源边际能量密度出现了两个极大值，且其最大值与最小值之间相差不大，从而可以看出细长药柱的能量定向性很差；延迟震源能量最大方向在0，主波束宽度为150°，可以看出其定向性比细长药柱要好；组合震源能量最大方向在0，主波束的宽度为60°，边际能量密度与延迟震源和细长药柱震源一样关于0两边对称；相控震源无论是平均边际能量密度还是最高边际能量密度相对于其他震源激发方式来说都是最大的，这也是相控震源激发方式优越性的原因，其定向性也比其他震源激发方式要好。

图6 不同震源激发方式叠加的地震波场快照

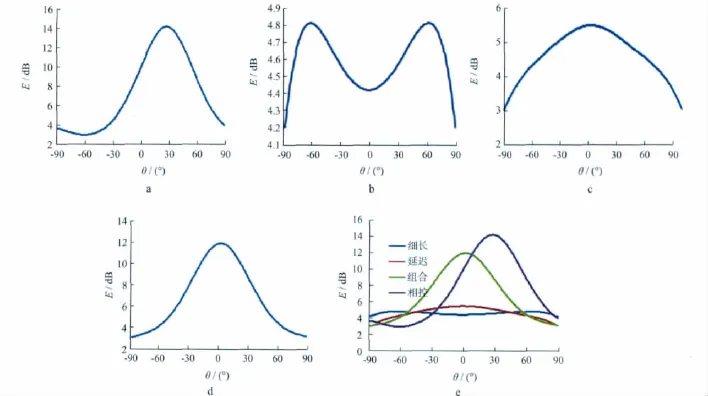
图7 不同震源激发方式的边际能量密度

2.1.2 激发效率的评判准则

根据震源对目标反射层的照射能量贡献［4］，将震源波场划分为4个区（图8）。由此我们可定义激发效率P为有效波场区能量与噪声波场区能量之比。

对于某个具体或特定工区的观测系统及激发方式，只要算出P值，即能判定激发方式的优劣。显然，P值越大震源激发效果越优。设一炮激发时对应的激发效率为P1，分层统计的相对激发效率为Pn／P1，即不同组合炮数时对应层接收到的组合震源能量与单一震源激发能量的比值。

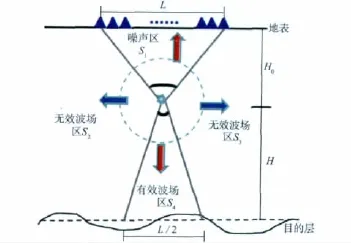
图8 震源波场能量分区示意［4－5］

利用边际能量密度求出不同震源激发方式的主波束方向以及能量汇聚带，然后利用图8计算出不同地质产状地震有效反射波的入射角范围，使其落入汇聚带以内；再利用不同激发方式的频率特性来限制基间距，延迟震源和细长药柱震源满足（n－1）·d≤15m时，其激发的地震子波频率不受压制；组合和相控震源满足（n－1）d≤20m时，组合震源产生地震子波基本不受压制，相控震源子波频率不受压制；最后利用激发效率的定义就可以求出相对激发效率最高的激发方式，即为最佳的震源激发方式。

2.2 模拟效果对比

2.2.1 水平地层模型

速度模型为4层，如图9所示，采用中间放炮两边接收，井深为5m。组合时炮点的间距为4m，为了更好地联系实际，取延迟震源与细长药柱震源的单节长度为1m。图10为对应不同激发方式的能量照明图，表1为不同震源激发方式的能量和相对激发效率。

图9 水平地层模型

由图10不同震源激发的照明可以看出：随着组合震源炮数的增加能量越来越集中，其深层的照明量越来越多且定向性越来越好，但当炮数到一定程度时，继续增加炮数其能量集中的程度变化已不再那么明显；细长药柱随着节数的增加下传能量基本不变，而延迟震源下传能量则有所增加。

图10 水平地层模型不同震源激发方式模拟的照明

表1 水平地层模型不同震源激发方式的模拟能量和相对激发效率

从表1可以看出，对于水平地层模型，组合震源随着炮数的增加，各层的相对激发效率明显增加，但对于不同深度其激发效率的改善程度是不同的。深层的激发效率比浅层的激发效率上升得快，即有利于能量向深层传递；但是，当炮数增加到一定程度时激发效率上升变缓，浅层的激发效率反而下降，对于此模型最佳的组合炮数从能量的角度选择为8炮。而对于延迟震源，其深层的相对激发效率比浅层要高，且随着级数的增加其相对激发效率在增加，但不是太明显。细长药柱震源增加级数后深层的相对激发效率反而变小，这说明细长药柱不利于深层勘探。

从图11和图12可以看出，8炮组合震源激发的浅层反射波明显有滞后的现象，且对浅层反射波主频以及频带宽度有明显的压制作用，因此，对于此模型的组合震源激发，其震源数应控制在8炮以内（即排列长度在28m以内）；经分析可知，当组合震源排列长度在20m以内时对子波的频率基本不压制，由此条件再根据震源激发产生的最大塑性区半径就可以选择最佳炮数与基距。

2.2.2 倾斜地层模型

速度模型为4层，如图13所示，采用中间放炮两边接收，井深为5m。组合时炮点的间距为4m，延迟和细长药柱震源基间距为1m，相控震源相邻震源间的井深差为1m。图14为不同震源激发方式的照明图。图15至图17为抽出的波形。图18为倾斜层不同震源激发方式叠加的振幅谱。表2为不同震源激发方式的能量和相对激发效率。

图14 倾斜地层模型不同震源激发方式模拟的照明

从图14a到图14d可以看出，对于倾斜地层，细长药柱震源的照明量最差；时延震源激发的照明量相对好；组合震源激发的照明量要比柱状震源和时延震源好很多；相控震源激发的照明量最好。在小倾角情况下，相控震源相对于组合震源的优势不是很明显。

图15 倾斜地层模型模拟记录第100道的波形

从图15到图17可以看出，在距离震源较近的地方，组合和相控震源产生的直达波能量较强，在距离震源较远的地方，各个震源产生的直达波能量相差不多；在震源的上倾方向，相控震源产生的反射波能量较强，在震源的下倾方向，组合震源产生的反射波能量较强，但随着层数的增加，组合震源与相控震源反射波能量之间的差距在减小。

从图18和表2可以看出，多炮分散激发时，有利于分辨率和信噪比（即表2中的相对激发效率数值）的改善，且不同震源激发方式对信噪比的改善程度不同。相控震源各个层的反射波能量都是最强的（即对信噪比的改善程度最好），组合震源次之，延迟震源再次之，细长药柱震源最差。但相对于水平地层细长药柱震源的激发效率在增加，这也证明了细长药柱震源能量向两边扩散的结论，所以对于倾斜地层建议采用相控震源激发。而在实际操作过程中，相控震源设计时应根据激发子波的波长、勘探目的层深度，通过其频率的压制特性、能量特性、激发效率特性，选择组合炮数、炮间距、激发井深、观测目的层段排列长度等参数来控制相控震源主能量方向、压制旁瓣等要素，使震源激发的地震波能量尽量多的落入观测目的层段范围内。

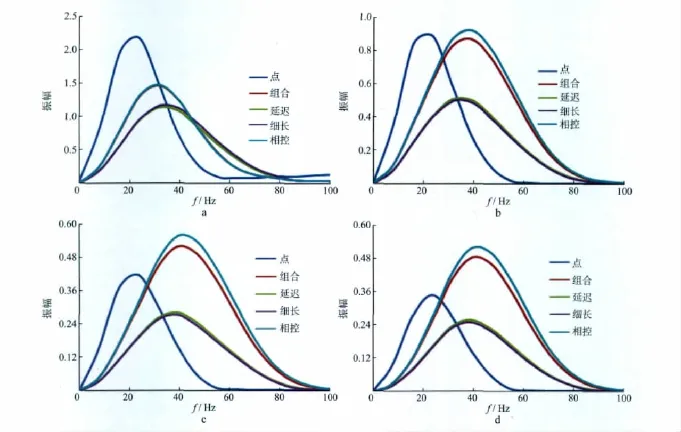
图18 倾斜地层模型不同震源激发方式模拟的叠加振幅谱

表2 不同震源激发方式的能量和相对激发效率

3 结束语

通过波动方程正演模拟对细长药柱震源、时延爆炸震源、相控爆炸震源以及水平组合震源激发方式进行了理论研究，通过不同激发方式的模拟波场对比，利用评判准则给出了水平和倾斜地层条件下相对最有效的激发方式。在研究相控震源时，利用能量照明图直观地给出了相控震源的定向性。根据模拟分析结果提出了不同激发方式在实际操作过程中所遇到的问题，并给出了有益的建议。

［1］胡立新，杨德宽，何兵寿，等.延迟爆炸法的理论分析［J］.石油地球物理探，2002，37（1）：33－38 Hu L X，Yang D K，He B S，et al.Theoretic analysis of delayed blast［J］.Oil Geophysical Prospecting，2002，37（1）：33－38

［2］徐淑合，于静，胡立新，等.多级延迟爆炸震源的研究与应用［J］.石油地球物理探，2003，38（4）：341－349 Xu S H，Yu J，Hu L X，et al.Research and application of Multi－stage delay explosion source［J］.Oil Geophysical Prospecting，2003，38（4）：341－349

［3］黄文尧，颜事龙，吕淑然，等.低爆速细长药柱的研究与应用［J］.爆破器材，2005，34（4）：18－22 Huang W Y，Yan S L，Lv S R，et al.The research and application of the low detonation velocity and elongated source charge［J］.Explosive Materials，2005，34（4）：18－22

［4］徐峰，刘福烈，梁向豪.基于相控理论的井炮组合设计技术［J］.石油地球物理勘探，2011，46（2）：170－175 Xu F，Liu F L，Liang X H.The source combination design technology based on the phased－array theory［J］.Oil Geophysical Prospecting，2011，46（2）：170－175

［5］汪仁富，徐峰，刘福烈，等.波动方程震源组合模拟定量研究［J］.石油地球物理勘探，2011，46（4）：538－544 Wang R F，Xu F，Liu F L，et al.The quantitative research of the wave equation source combination simulation［J］.Oil Geophysical Prospecting，2011，46（4）：538－544

［6］姜弢，林君，陈祖斌，等.相控震源地震波定向技术［J］.吉林大学学报（信息科学版），2004，22（3）：181－184 Jiang T，Lin J，Chen Z B，et al.Seismic beam－forming in phased－array Vibroseises［J］.Journal of Jilin University（Information Science Edition），2004，22（3）：181－184

［7］姜弢，林君，杨东，等.相控震源定向地震波信号分析［J］.地球物理学报，2008，51（5）：1551－1556 Jiang T，Lin J，Yang D，et al.Analysis of direction seismic signal based on phase－array vibrator system［J］.Chinese Journal of Geophysics，2008，51（5）：1551－1556

［8］姜弢.基于相控震源的地震波定向方法研究［D］.长春：吉林大学，2006 Jiang T.Study on seismic beam－forming method based on phased－array vibrator system［D］.Chang chun：Ji Lin Univesity，2006

［9］Alford R M，Kelly K R，Boore D M.Accuracy of finite－difference modeling of acoustic－wave equation［J］.Geophysics，1974，39（6）：834－842

［10］Hastings F D，Schneider J B，Broschat S L.Application of the perfectly matched layer（PML）absorbing boundary condition to elastic wave propagation［J］.Journal of the Acoustical Society of America，1996，100（5）：3061－3069

［11］王忠仁，林君，冯声涯.地震勘探中相控阵震源的方向特性研究［J］.地球物理学报，2006，49 （4）：1191－1197 Wang Z R，L J，Feng S Y.Directivity of phase array vibrators in seismic exploration［J］.Chinese Journal of Geophysics，2006，49 （4）：1191－1197