地面微地震监测资料静校正方法研究

姜宇东，宋维琪，郭晓中，刘太伟，冯 超

（1.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103；2.中国石油大学（华东）地球科学与技术学院，山东青岛266580）

由于地面微地震监测检波器布设在地表，微地震有效事件的初至会受到地表起伏和低降速带厚度变化的影响。这些影响不利于微地震资料提高信噪比的处理效果［1－2］，还会影响最终微地震有效事件定位结果的精度。

实际地面微地震监测资料处理中假设：每个微地震事件所用到的静校正量都是由检波器位置所决定的，也就是说每个微地震事件使用的静校正量都是相同的。由于测线覆盖面积相对较广，而产生微地震事件的破裂源分布范围有限，不同事件传播路径之间不会有巨大变化。因此，通常情况下这个假设是成立的。

由于缺少表层速度信息，因此相对于常规地震资料来说，地面微地震资料的静校正处理难度更大［3－4］。目前，在国内外相关研究中，地面微地震资料的静校正量要靠射孔事件的信息来求取。射孔事件是射孔弹在已知位置进行强能量激发产生并由地面微地震资料采集系统接收到的地震信号。射孔事件能量要比大部分微地震事件的能量强，在记录资料中易于识别，所以其初至走时大多可以拾取。这与井中微地震监测方法相同。不同的是，由于井中微地震资料的信噪比较高，几乎在每一个记录道上都能准确地拾取到射孔事件的相应走时；而地面微地震资料的信噪比很低，微地震信号能量弱，并不是每个记录道上都能拾取到准确的初至走时。

针对上述情况，尝试利用已知的射孔位置与射孔事件初至走时，通过迭代调整地层速度模型，再根据射孔事件初至走时，计算各条测线上记录道的静校正量。

1 静校正方法

1.1 初至拾取方法

1.1.1 射孔事件初至拾取与校正

初至拾取是近地表静校正的前提和基础，初至拾取的精确程度直接影响静校正质量的好坏，尤其是在地表起伏以及速度变化剧烈的地区，初至波的精确拾取尤为重要。

由于实际地面微地震数据信噪比通常很低，常用的自动初至拾取方法拾取的事件初至精度往往较差。并且，每个事件能够准确拾取初至的记录道是有限的，使得能求取静校正量的记录道数很少，或者不连续。在微地震波传播过程中，由于不同事件的传播路径的不同，其静校正值往往不一样。造成的典型现象是用射孔和某些微地震强事件算出的静校正量［5－7］应用到其它强事件中去时，事件同相轴经过校正后并不是呈严格的水平直线，而在局部存在抖动。

由于微地震资料初至拾取的这些特点，需要对初步拾取的走时进行校正。首先用人工初步拾取的初至校正对应的强事件数据，如果拾取的走时是完全准确的，则经校正后的有效事件同相轴完全水平，在各道上的初至波相位是一样的，那么用一个标准子波对每道数据做互相关时，变量为走时的互相关函数的最大值所对应的走时。如果拾取的走时存在扰动，则扰动量即为互相关函数最大值对应走时与标准值的差值。在实际处理中，一个标准的事件子波是得不到的，而且不同事件的子波波形也不相同。基于此，选定一个初至拾取较准确即信噪比较高的道作为标准道，在这个道对应初至的地方选取一个合适大小的时窗，用该时窗道与测线中的每一道进行互相关运算，得到与最大互相关值对应的时移量是一样的，在对每一道做时移后，将每一条测线的所有道叠加起来就得到一个初始引导道。然后，用此引导道与测线中的所有道做互相关。如此往复，直到最后算出的时移量达到要求。图1为微地震原始记录预处理剖面。图2为用强能量微地震事件初步拾取到的初至对原始数据进行拉平后的结果，可以看到利用初步拾取的初至进行拉平后的剖面局部存在着一些抖动。图3为应用校正后的初至对原始数据进行拉平后的结果，显示拉平后这些抖动得到了纠正。由拉平后的同相轴的一致性可以看出校正后的初至信息更加准确。

1.1.2 强能量有效事件初至拾取

对于射孔事件，通常不可能在全部记录道中都拾取到初至走时。因此，计算出的静校正量是部分道的，将其应用到实际数据时，虽然可以对这些道数据进行校正，但是当道数较少或者不连续时，对处理的影响较大。考虑到地面微地震数据中有一些比较强的微地震事件，可将这些强微地震事件的初至拾取后，用射孔事件走时算出的速度模型进行基于走时的反演，计算出这些强事件的理论走时，从而得到这些强事件拾取道所对应的静校正量。这样，通过射孔事件和部分强事件，就可得到大多数记录道的静校正量。

1.1.3 利用叠加处理资料拾取初至

在未进行叠加处理的微地震资料上拾取的初至包含了局部和区域的微地震波走时信息，这种初至拾取方法固然精度较高，但是初至拾取过程太繁琐。另一方面，即便是准确地拾取了初至，因其包含了局部和区域的微地震波走时信息，进行校正量计算时未必能准确地利用这个局部走时信息，因为局部走时信息是由局部不均匀速度引起的，而这个局部速度模型很难建立。如果通过叠加或拟合处理，在把局部初至走时信息去掉的同时，又不影响区域初至走时信息，则利用区域初至走时更容易进行静校正量的计算。其实，事件的初至走时信息应该是区域信息，局部走时信息只是干扰信息，可作为剩余静校正量。

根据地震波传播理论，微地震事件地面记录的时距曲线是二次曲线，可设计二次曲线叠加方法。对实际资料进行叠加处理，叠加原则是沿着期望初至方向达到叠加能量最大，且互相关最大。叠加窗口的大小应随着不同局部干扰空间范围而不同，如果局部干扰空间横向范围大，则叠加窗口应随之增大。

1.2 利用射孔资料进行静校正量计算

对于地面微地震监测，观测测线高程随地形变化，并不在一个水平面上，而且，由于声波测井资料缺乏浅层数据，以及地表风化层、低降速带资料和近地表速度均未知，导致静校正量难以确定，给资料处理以及微地震事件反演定位造成了困难。

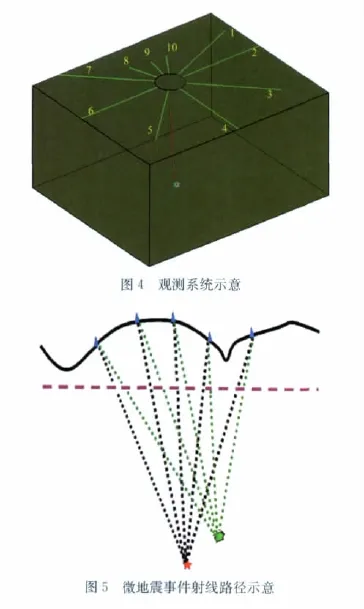
为此，需要针对这种情况，进行静校正处理方法研究。以一实际微地震监测为例，观测系统如图4所示，10条地面测线呈放射状排列。图5为微地震事件射线路径示意图，红色点为射孔点，绿色点为某一微地震事件点位置，蓝色三角形为地面检波点，曲线为地表观测面，紫色虚线为水平基准面。如前所述，由于基准面至地表的地层速度未知，导致静校正量无法直接确定。这里将借助射孔资料进行静校正量计算。

1.2.1 射孔事件实际走时差

针对不同测线，分别拾取各测线上的射孔事件初至，根据拾取的各测线上的射孔初至tperf（i），计算相邻检波器的射孔事件走时差dtperf（i），i为道号。

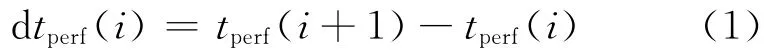
1.2.2 射孔事件理论走时差

根据声波测井资料建立初始水平层状速度模型，通过射线追踪正演方法，求取射孔事件理论走时tm（i），计算相邻观测点在基准面上的射孔事件理论走时差dtm（i），i为道号。

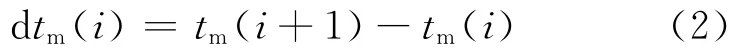
1.2.3 初始静校正量

实际射孔记录的初至走时差减去理论计算的射孔点的初至走时差，作为初始静正量δt0（i），即

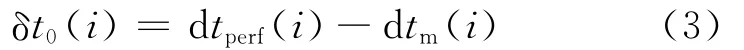
1.2.4 静校正量的反演校正

由于利用测井声波时差建立的速度模型和实际的速度模型不尽相同［8－10］，必然存在一定的误差，因此，计算的理论初至走时也存在误差，为了使这个误差尽量小，利用反演方法进行速度模型调整。速度模型调整得越精确，计算的走时就越准确，静校正量的计算也就越精确。

一般情况下，浅层速度变化比深层速度变化对走时曲线的影响大，因此，建立准确的浅层速度模型更为重要。为此，在建立速度模型时，将浅层速度模型建立为二维速度模型，深层速度模型建立为一维水平层状速度模型。这里把测井声波时差范围内（基准面以下）的速度视为深层速度模型，其上的速度模型作为浅层速度模型。

浅部地层的速度较低，假定在基准面之上的地震波的射线近似垂直于水平面，则浅部地层初始速度为

式中：i为道号；m 为总道数；h（i）为基准面到第i检波器处地表观测面的高度。

为了求取最佳静校正量，利用反演方法，通过浅部和深部地层速度模型的不断调整，使理论计算的整个地层速度模型下的理论走时差和实际射孔走时差的均方差值最小，即

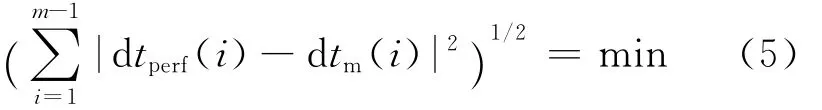
1.3 总静校正量计算

速度模型校正后的正演走时与实际观测的射孔事件拾取走时对比结果如图6所示。校正后速度模型的正演走时不可能与实际走时完全吻合，即反演迭代最终误差不可能为零，将这个不为零的误差视为剩余静校正量ε（i）［11］。高程静校正量Δth（i）等于检波器高度h（i）除以校正后的浅层速度vq。总校正量为剩余静校正量与高程静校正量之和［12］，即

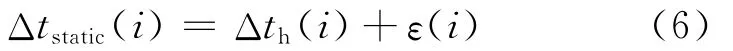
具体的静校正值计算流程为：

1）通过声波测井资料，建立基准面以下的深部初始速度模型；

2）拾取各条测线的射孔事件初至；

3）利用射孔初至减去基准面之下的理论初至得到初始静校正量；

4）利用初始静校正量建立浅部地层初始速度模型；

5）利用反演方法调整地层速度模型和静校正量；

6）如果达到误差精度，则输出速度模型与静校正量；若未达到误差精度，则返回步骤5）；

7）输出总静校正量。

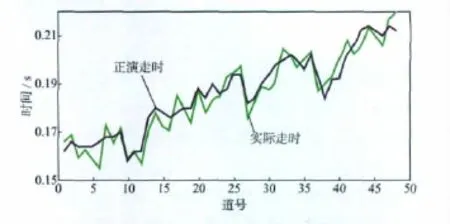
图6 速度模型校正之后正演走时与实际走时对比

2 实际应用效果分析

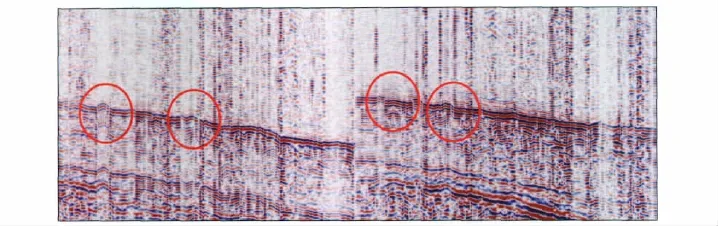
图7 静校正前地面微地震数据（两相邻测线）

按照上述静校正量计算流程，得到了大部分数据道对应的静校正量。为了验证求取静校正量方法的正确性，进行了实际微地震监测数据的静校正处理试验。图7为静校正之前的地面微地震剖面。为了方便显示，选取了其中2条测线。从校正前的数据剖面可以看出同相轴局部抖动相当严重（红圈）。图8为静校正处理后的地面微地震数据剖面。从静校正处理前后结果的对比可以看出，通过计算出的静校正量将原先起伏的有效事件同相轴校正为符合透射波走时的双曲线形状，处理后的剖面面貌得到明显改善，局部抖动不再存在。

图8 静校正后地面微地震数据（两相邻测线）

3 结束语

对于地面微地震监测资料，接收到的有效事件一般为透射波，信噪比低，甚至出现看不到同相轴的情况，因此，初至难以拾取。由于表层速度资料的缺乏，很难利用常规的方法进行地面微地震资料的静校正。本文提出的引导道方法可以拾取不可见同相轴的记录道初至。由于浅层速度变化比深层速度变化对走时曲线的影响大，在建立速度模型时，浅层速度模型采用二维速度模型，深层速度模型采用一维水平层状速度模型，较好地体现不同深度速度变化对初至时间的影响。同时，速度的反演校正过程也分为相对应的两部分，避免反演迭代时由于深、浅部速度变化不同，使得变化相对大的数据吃掉变化小的数据，从而提高反演的敏感性和精度。根据初至走时和声波测井资料反演出地下速度模型，同时得到近地表速度模型。由速度模型正演得到的理论走时和事件实际走时的残差作为剩余静校正量，高程静校正量与剩余静校正量之和即为总静校正量。实际地面微地震数据的处理结果验证了本文所研究静校正方法的应用效果。

［1］王彦春，余钦范，李峰，等.交互迭代静校正方法［J］.石油物探，1998，37（2）：63－70 Wang Y C，Yu Q F，L F，et al.The method of static correction by interactive iteration［J］.Geophysical Prospecting for Petroleum，1998，37（2）：63－70

［2］王克斌，王顺根.利用扩展广义互换折射波静校正方法解决MX地区资料的野外静校正闭合差 ［J］.石油物探，2001，40（2）：126－130 Wang K B，Wang X G.Solving the mis－tie problem in MX area via extended generalized reciprocal method （EGRM）refraction statics ［J］.Geophysical Prospecting for Petroleum，2001，40（2）：126－130

［3］朱卫红，郑伟建，金晓雷，等.折射静校正在三维地震资料处理中的应用［J］.石油物探，1999，38（3）：39－44 Zhu W H，Zheng W J，Jin X L，et al.Application of refraction static correction to 3－D seismic data processing［J］.Geophysical Prospecting for Petroleum，1999，38（3）：39－44

［4］薛为平，刘治凡，周清华，等.准噶尔盆地南缘山地静校正方法探讨［J］.新疆石油地质，2003，24（6）：576－578 Xue W P，Liu Z F，Zhou Q H，et al.Discussion of static correction approaches for mountains in Southern Margin of Junggar Basin［J］.Xinjiang Petroleum Geology，2003，24（6）：576－578

［5］李家康，余钦范.近地表速度的约束层析反演 ［J］.石油地球物理勘探，2001，36（2）：135－140 Li J K，Yu Q F.Constrained tomographic inversion for near－surface velocity ［J］.Oil Geophysical Prospecting，2001，36（2）：135－140

［6］王孝，禄娟，冯心远，等.先验信息约束层析成像静校正技术在柴西南地区的应用［J］.石油物探，2010，49（1）：30－33 Wang X，Lu J，Feng X Y，et al.Application of priori information constraint tomography static correction technique in the south of Western Qaidam basin［J］.Geophysical Prospecting for Petroleum，2010，49（1）：30－33

［7］王孝，贺振华，王述江，等.多信息约束层析反演静校正技术及其应用［J］.天然气地球科学，2010，21（2）：316－320 Wang X，He Z H，Wang S J，et al.Technology of static correction for multi－information constrained tomographic inversion and its application［J］.Natural Gas Geoscience，2010，21（2）：316－320

［8］李辉峰，邹强.非地表一致性静校正方法探讨［J］.石油地球物理勘探，2005，40（S1）：128－137 Li H F，Zu Q.Discussion on the method of surface nonconsistent static corrections［J］.Oil Geophysical Prospecting，2005，40（S1）：128－137

［9］王振华，袁明生，阎玉魁，等.复杂地表条件下的静校正方法［J］.石油地球物理勘探，2003，38（5）：487－500 Wang Z H，Yuan M S，Yan Y Q，et al.Method of static corrections under complex near－surface conditions［J］.Oil Geophysical Prospecting，2003，38（5）：487－500

［10］郑鸿明，彭勇，蒋琳，等.时变校正方法研究与应用［J］.新疆地质，2009，27（1）89－91 Zheng H M，Peng Y，Jiang L，et al.The research and application to time－variant corrections method［J］.Xinjiang Geology，2009，27（1）：89－91

［11］吴波，潘树林，陈辉.用四阶累积量子函数改进剩余静校正量的计算［J］.石油物探，2010，49（3）：227－239 Wu B，Pan S L，Chen H.Improvement of calculating residual statics by fourth－order cumulant subfunction ［J］.Geophysical Prospecting for Petroleum，2010，49（3）：227－239

［12］刘文革.整体波场延拓法基准面校正与常规方法对比［J］.西南石油大学学报（自然科学版），2010，32（6）：57－64 Liu W G.A comparative study between global wavefield continuation and routine methods for datum correction［J］.Journal of Southwest Petroleum University（Science ＆ Technology Edition），2010，32（6）：57－64