人工气候环境下混凝土内相对湿度响应预测

蒋建华，袁迎曙，王嵩林，孙冬林

(1. 河海大学 土木与交通学院，江苏 南京，210098；2. 中国矿业大学 力学与建筑工程学院，江苏 徐州，221116；3. 上海众谊建筑设计有限公司，上海，200092)

混凝土含湿量是影响混凝土结构耐久性及高温性能的重要因素[1−3]。而表层混凝土的传湿性能决定了内部含湿量变化，混凝土传湿性能的研究对于研究气候环境对混凝土结构作用定量模式及耐久性退化规律预测具有重要意义。表征混凝土传湿能力的指标为湿气扩散系数。李魁山等[4]测试了多种建筑材料的湿气扩散系数，指出湿气扩散系数随试样两侧的湿度差而呈指数形式增长；黄达海等[5]测量了等温环境下混凝土向非饱和空气介质传湿的全过程，发现混凝土的湿气扩散系数严重依赖于混凝土内相对湿度；Delgado[6]利用非稳态湿气吸附试验得到4种不同建筑材料的湿气扩散系数，并考虑不同温度、相对湿度变化(湿度差)的影响。关于混凝土内相对湿度的研究，Norris等[7−9]对混凝土内相对湿度的监测技术展开了研究；马文彬等[10−13]则开展了气候环境对混凝土内相对湿度的影响研究。虽然相关研究揭示了混凝土湿气扩散系数的部分变化规律，但影响因素考虑不够全面，未建立混凝土湿气扩散系数的计算模型；混凝土内相对湿度的响应规律及其预测研究还有待深入。本文首先在恒定温湿度的人工气候环境下，开展混凝土内微环境相对湿度的响应试验，然后，基于相对湿度响应试验结果以及传质学基本理论，计算各种试验条件下的混凝土湿气扩散系数，并研究环境风速对混凝土传湿过程的影响；基于混凝土湿气扩散系数的变化，提出混凝土等效湿气扩散系数的概念及计算模型。最后，基于混凝土传质过程的基本理论以及湿气扩散系数的研究成果，建立人工气候环境下混凝土内相对湿度响应预测模型。

1 人工气候环境下混凝土相对湿度响应试验

1.1 试件设计

试件采用C25混凝土，水泥、砂子、石子、水质量比为1:1.6:2.96:0.54。水泥采用P.O 42.5普通硅酸盐水泥；细骨料为河砂(中砂)，细度模数为2.7；粗骨料为碎石，其主要成分为石灰岩和粗面岩，粒径为5～15 mm，级配良好；水为普通自来水。

试件长×宽×高为100 mm×150 mm×250 mm，浇筑混凝土时，利用塑料管在试件内预留孔洞，预留孔平行于混凝土试件的暴露面，孔距混凝土表面的距离为25 mm。试件的相关尺寸及制作如图1所示。

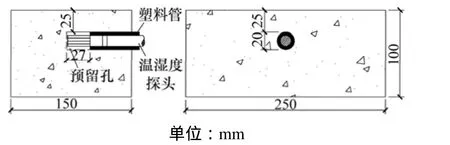
图1 湿度响应试件设计Fig. 1 Specimen design for response of relative humidity

1.2 试验过程与方法

1.2.1 相对湿度正向响应

恒温条件下，当混凝土内部相对湿度低于环境相对湿度时，在湿度梯度的作用下，湿气自混凝土表面向内部传输，混凝土处于吸湿状态，本文将此过程定义为混凝土相对湿度正向响应。

混凝土试件浇筑、养护完成后，试验之前，首先利用烘箱将混凝土试件适度烘干，然后将试件置于恒定温湿度环境中，采用温湿度传感器监测混凝土内部温湿度条件，最终使混凝土内相对湿度在试验温度下达到65%左右。

试件处理完毕后，用塑料管和密封胶将温湿度探头埋置到预留孔中(如图 1所示)。同时，为了模拟混凝土湿气的单向传输，除试件暴露表面外，其余表面采用塑料薄膜和环氧树脂密封。之后将试件放入已设置好温度、相对湿度条件的小型人工气候箱内，定时记录温湿度探头的相对湿度变化。试验进行至混凝土内相对湿度与环境相对湿度基本平衡为止。各种温湿度气候条件的试验均重复以上过程。试验条件组合见表1。

1.2.2 相对湿度反向响应

恒温条件下，当混凝土内部相对湿度高于环境湿度时，混凝土处于干燥状态，本文将此过程定义为混凝土相对湿度反向响应。反向响应试验过程与方法，与正向响应试验基本相同，只是混凝土试件内外环境的初始湿度条件有所区别。为了实现混凝土内湿气反向(向外)传输，首先通过高湿环境将混凝土内初始相对湿度控制在(95±1)%(对应试验温度)，而试验环境设定为高温、低湿条件。反向响应试验中，人工气候环境温、湿度条件组合见表1。

1.3 试验结果与分析

根据实测数据绘制出不同试验条件下，混凝土内部25 mm深度位置处相对湿度随时间的变化曲线，部分结果如图2所示。

试验结果表明：(1) 混凝土内相对湿度明显滞后于环境相对湿度，内部湿度达到与环境湿度相平衡，需要一段较长时间。其原因是：(1) 混凝土内外湿度响应实质为表层混凝土的传湿过程，混凝土材料自身孔结构具有一定密实性，混凝土传湿是一个相对缓慢的过程；(2) 正向或反向响应过程中，混凝土温度相同时，混凝土内外初始相对湿度差(ΔH0=|He−H0|)越大，混凝土内相对湿度响应越快，因为混凝土内外湿度差是湿气在混凝土内部传输的驱动力；(3) 与正向响应相比，混凝土内相对湿度反向响应滞后更加显著。虽然湿气在混凝土内传输的机理以扩散为主，但同时还存在毛细吸附作用。在正向响应过程中，毛细吸附可以加速湿气向混凝土内传输；在反向响应过程中，则产生抑制作用。

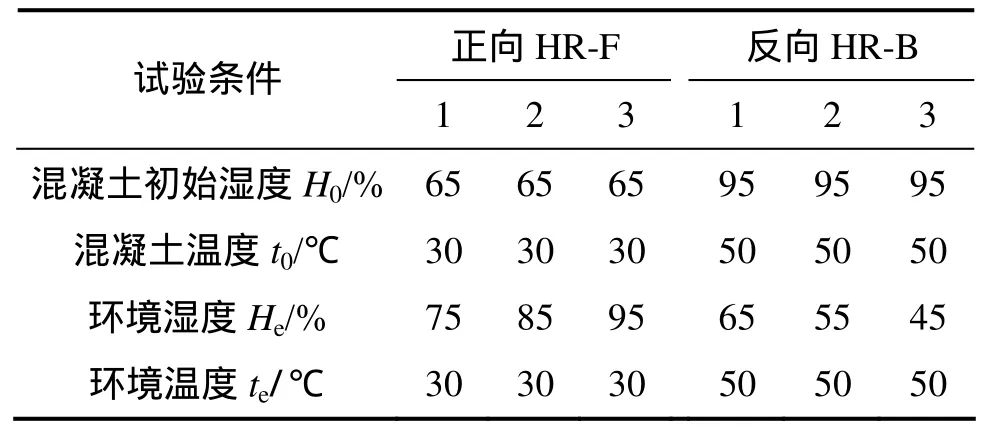
表1 试验条件组合Table 1 Combinations of test conditions

图2 混凝土内相对湿度响应曲线Fig. 2 Response curves of relative humidity in concrete

2 混凝土湿气扩散系数

2.1 湿气扩散系数的计算理论

混凝土内相对湿度响应过程的主要机理为湿气在混凝土内的扩散。从浓度变化角度可将固体中的扩散分为稳态扩散与非稳态扩散。混凝土相对湿度响应的试验结果证明：混凝土的湿气传输归结为非稳态扩散。根据传质学理论，非稳态扩散问题的控制方程为菲克扩散第二定律，其数学表达式如下[14]：

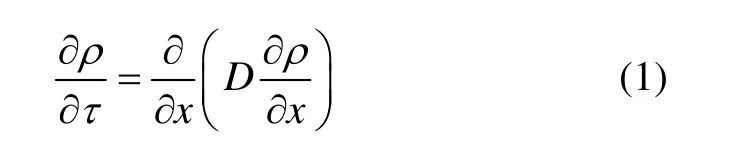
式中：ρ为扩散组元的质量浓度，kg/m3；D为扩散系数，m2/s；τ为扩散时间，s；x为内部某一截面距离固体表面的深度，m。

实际的固体扩散中，扩散系数通常是随浓度和位置而改变的变值。采用变量代换法，对式(1)进行求解，得到扩散系数的理论表达式为

于是，基于式(2)，将混凝土内相对湿度H视为扩散物质浓度C，令混凝土内初始相对湿度为H0，响应过程时刻末对应的混凝土内相对湿度为Hf，则混凝土的湿气扩散系数计算表达式为

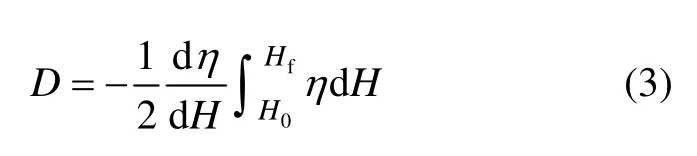
2.2 正向湿气扩散系数

混凝土内深度x一定时，η仅为时间τ的函数。因此，只要利用试验方法确定混凝土试件内某一特定截面上相对湿度H随时间τ的变化规律，就可以利用式(3)计算D。

图 3所示为不同混凝土内外初始湿度差(ΔH0)情况下，混凝土内不同相对湿度时对应的正向湿气扩散系数DF的计算结果。

同时，为了充实混凝土正向湿气扩散系数的试验数据，利用孙红萍[15]的试验结果(ΔH0=30%)进行计算，得到不同温度(T)和水灰比(w/c)组合条件下，混凝土内不同相对湿度时对应的DF，见表2。

综合图3和表2中的结果表明：混凝土正向湿气扩散系数DF随混凝土内相对湿度H而变化，同时还受到混凝土水灰比w/c、温度t和初始湿度差ΔH0影响。其他条件一定时，H越大，DF越小；w/c，t和ΔH0越大，DF越大。

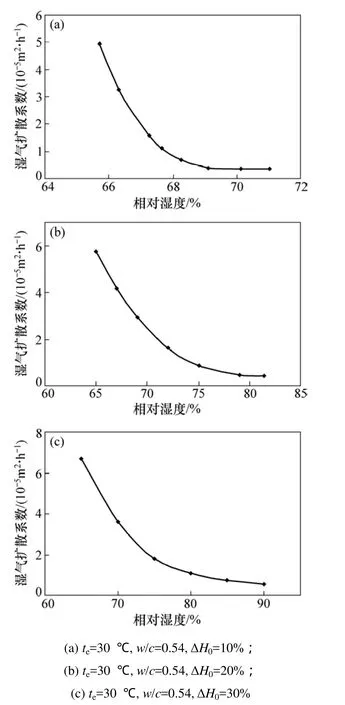
图3 正向湿气扩散系数演变规律Fig. 3 Changes in forward diffusion coefficients of moisture

2.3 反向湿气扩散系数

基于人工气候环境下混凝土内相对湿度反向响应试验结果，利用式(3)计算混凝土反向湿气扩散系数DB，计算结果如图4所示。

不同混凝土温度和水灰比组合条件下，混凝土内不同相对湿度时对应的DB，见表3。

综合图4和表3可见：混凝土反向湿气扩散系数DB随混凝土内相对湿度H的升高而增大，同时也受到混凝土水灰比w/c、温度t和初始湿度差ΔH0影响；其他条件一定时，w/c，t和ΔH0越大，DB越大；与混凝土相对湿度正向响应相比，在混凝土w/c，t，ΔH0以及H相同的条件下，混凝土的反向湿气扩散系数DB明显小于正向湿气扩散系数DF。

表2 不同条件下混凝土正向湿气扩散系数Table 2 Forward diffusion coefficients of moisture in concrete under different conditions 10−6 m2/h

表3 不同条件下混凝土反向湿气扩散系数(×10−6 m2/h)Table 3 Backward diffusion coefficients of moisture in concrete under different conditions

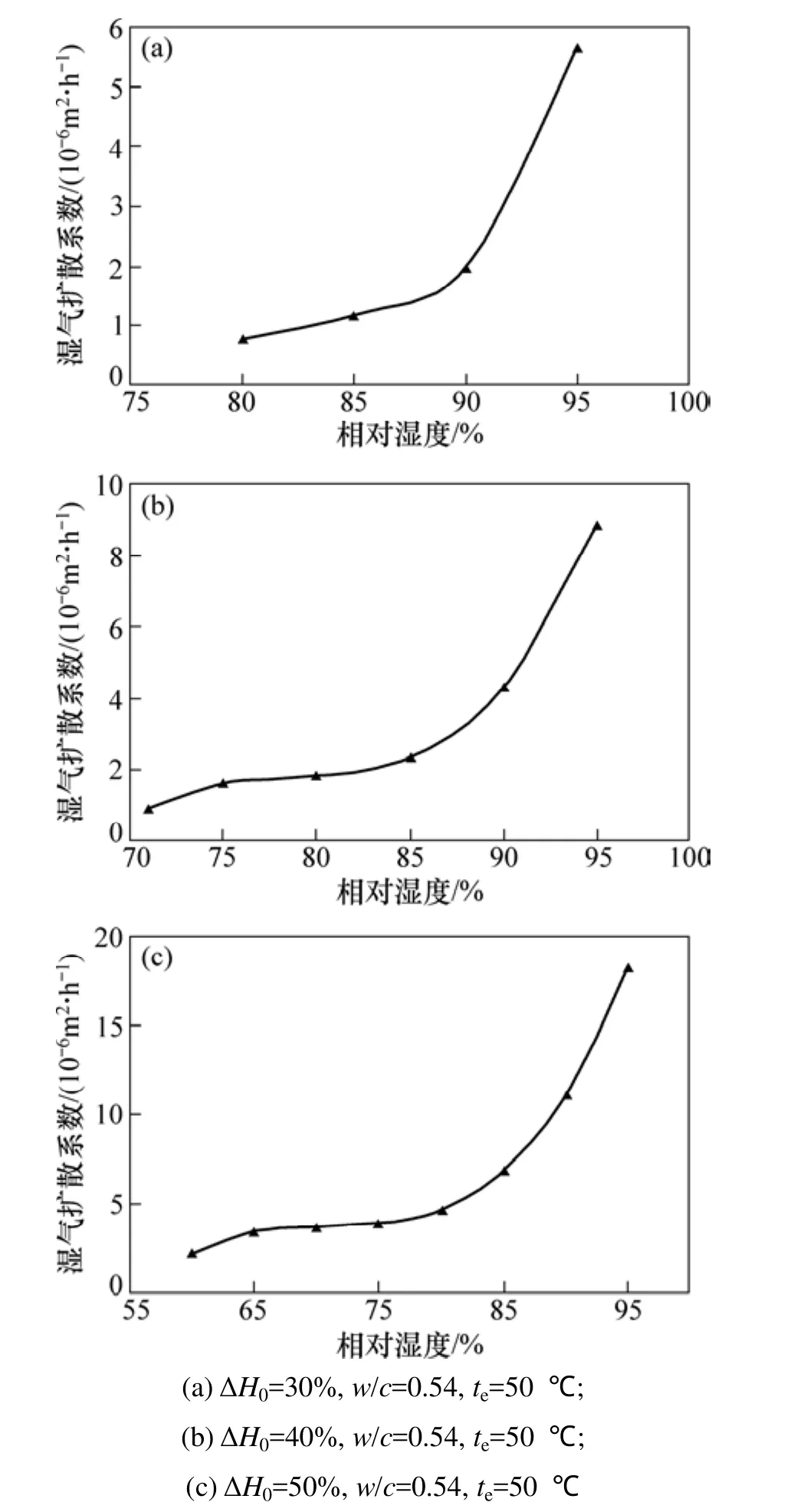
图4 反向湿气扩散系数演变规律Fig. 4 Changes in backward diffusion coefficients of moisture

3 环境风速对湿气扩散系数的影响

实际自然气候环境下，混凝土结构表面空气处于流动状态。当混凝土内部湿度较大时，环境风速将加快混凝土内部湿气向外传输。

3.1 风速影响的试验研究

采用与1.1节中相同的试件设计，但试件混凝土包含3种不同等级，水灰比(w/c)分别为0.62，0.54和0.48。为了研究环境风速对混凝土内相对湿度反向响应的影响，本文设计了一套模拟环境风速作用的试验装置。该装置通过调压仪来控制风机的不同转速，从而实现不同风速，并利用风速测定仪实时显示当前的风速。

整个试验装置位于人工气候环境室内(温度为(30±1) ℃、相对湿度为(70±3)%，装置内环境与人工气候室环境相同。在试验过程中，在不同风速vw(4.2 m/s，6.6 m/s和8.5 m/s)作用下，持续记录混凝土内25 mm深度处相对湿度随时间的变化，部分记录结果如图5所示。

图5 风速作用下混凝土内相对湿度响应曲线Fig. 5 Response curves of relative humidity in concrete under wind speed

模拟环境风速影响的试验结果表明：(1) 风速对混凝土内湿气的反向扩散影响明显，环境风速越大，混凝土内湿气反向扩散就越快；同时，环境风速越大，混凝土水灰比对湿气反向传输速率的影响越显著；(2) 风速对混凝土湿气反向传输影响的大小，与混凝土的水灰比相关，混凝土水灰比越大，风速对湿气反向传输的影响越显著。

3.2 考虑风速影响的混凝土反向湿气扩散系数

加快混凝土表面的空气流动速度(风速)能够使蒸发界面上的空气层变薄，加强热量的传递和水蒸气向外的扩散，从而提升混凝土的干燥速率。环境风速对混凝土相对湿度反向响应的影响可以体现在反向湿气扩散系数上。

基于风速作用下的混凝土相对湿度反向响应试验结果，利用式(3)计算对应的混凝土反向湿气扩散系数DB，部分计算结果如表4所示。

表4 不同风速下混凝土反向湿气扩散系数Table 4 Backward diffusion coefficients of moisture in concrete under different wind speeds 10−7 m2/h

从表4可以看出：混凝土水灰比、含湿状态和环境风速对混凝土反向湿气扩散系数均存在影响。其他条件相同的情况下，w/c越小，DB越小；vw和H越大，DB越大。

环境风速对混凝土反向湿气扩散系数的影响基本服从指数函数规律。若在风速vw=0的条件下，混凝土反向湿气扩散系数记为D0，则考虑风速影响的反向湿气扩散系数DBw可表达为：

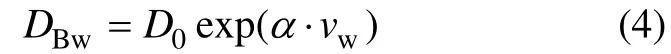
式中：vw为环境风速，m/s；α定义为环境风速影响系数，是混凝土水灰比的函数，α=2.195×(w/c)−0.835。

4 等效湿气扩散系数

图 6所示为混凝土试件相对湿度正向响应(HR-F-1)和反向响应(HR-B-1)过程中，混凝土湿气扩散系数随时间的变化。从图6可以看出：在整个湿度响应时间段内，混凝土湿气扩散系数不断下降，前期下降速率较快，后期逐渐逼近于 0，这主要与混凝土内湿度梯度的变化有关。

鉴于湿气扩散系数的变化，为了建立混凝土内相对湿度响应预测模型，本文提出混凝土等效湿气扩散

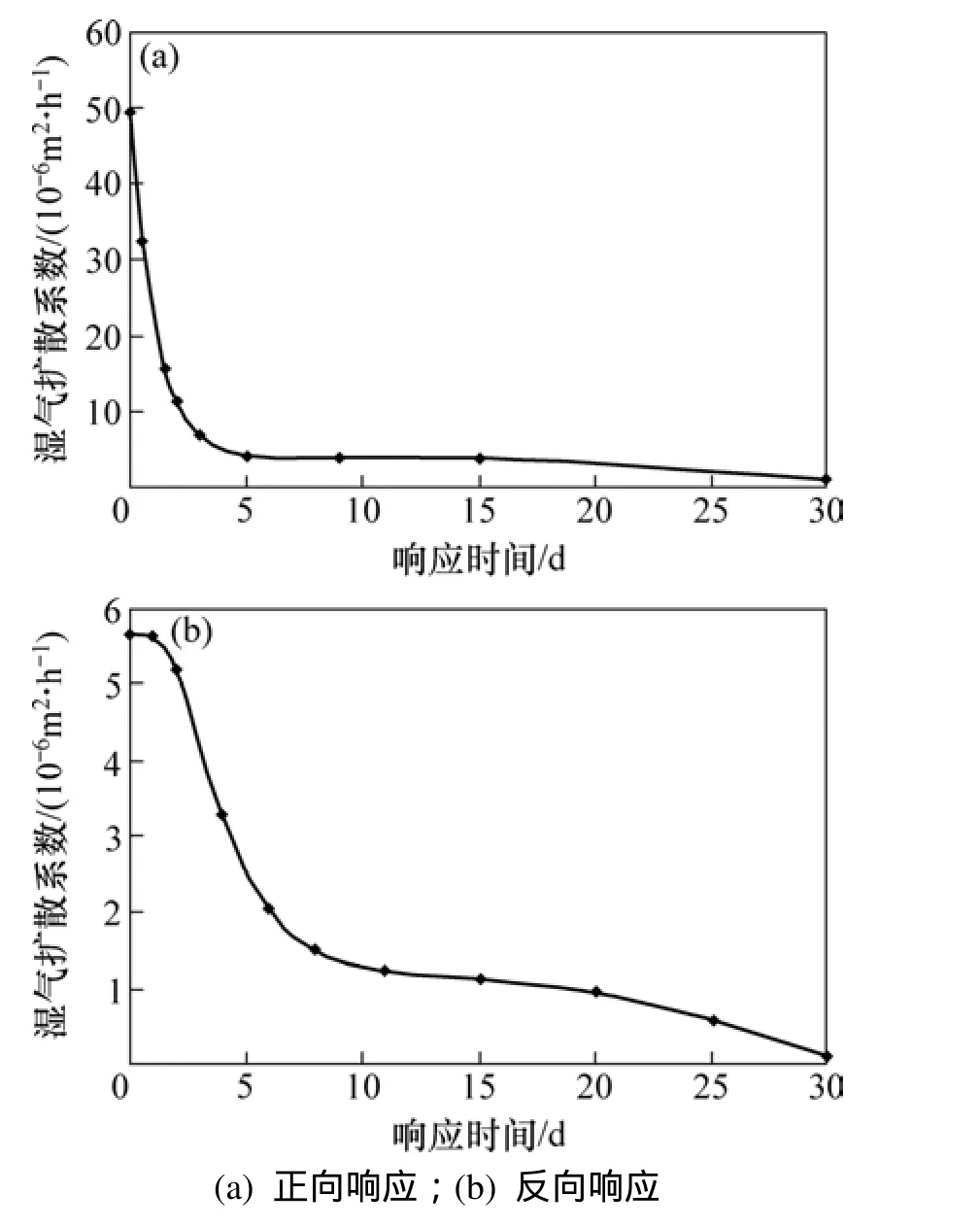
图6 混凝土湿气扩散系数随时间演变规律Fig. 6 Changes in diffusion coefficients of moisture with time

系数的概念。若将混凝土相对湿度响应过程的时段记为(0，τ)，对该时间区间的湿气扩散系数积分，并取其积分平均值，即

式中：τ为混凝土内相对湿度响应时间。本文将定义为混凝土的等效湿气扩散系数。

按照定义式(5)，并基于上述混凝土湿气扩散系数计算结果，得到了不同试验条件下混凝土的等效湿气扩散系数。图 7所示为不同初始相对湿度差 ΔH0影响下的混凝土。

从图7可以看出：混凝土随着ΔH0的升高而增大，且两者服从指数函数关系。

表5和6所示为考虑混凝土水灰比w/c和温度t影响的混凝土正向、反向等效湿气扩散系数。

从表5和表6可见：w/c和t均是混凝土等效湿气扩散系数

D的重要影响因素。总体而言，w/c和t越大，越大。

综上所述，混凝土等效湿气扩散系数的影响因素主要包括混凝土w/c，t和ΔH0。本文借助 DataFit软件对混凝土等效湿气扩散系数的计算结果进行多元非线性回归分析，从而确立其计算模型，分别如式(6)和(7)所示。

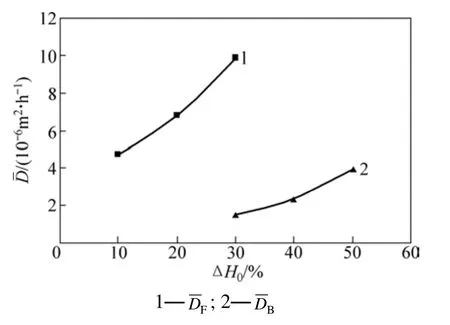
图7 初始湿度差对等效湿气扩散系数的影响Fig. 7 Effects of ΔH0 on equivalent diffusion coefficients of moisture

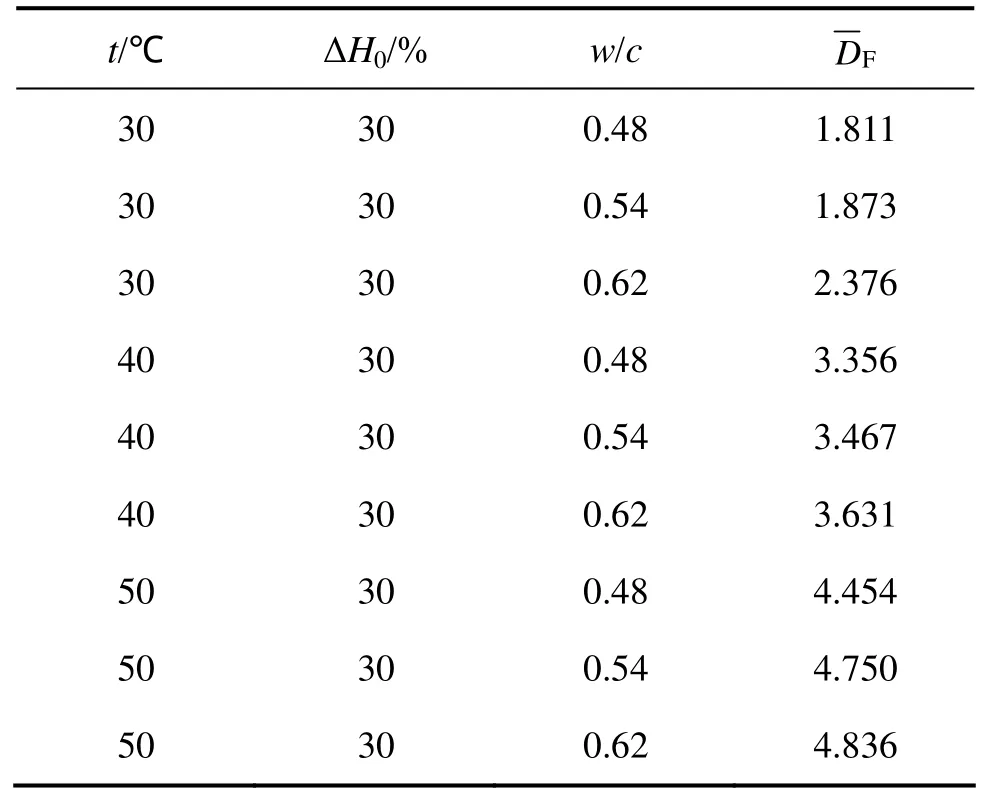
表5 混凝土正向等效湿气扩散系数Table 5 Equivalent forward diffusion coefficients of moisture in concrete 10−6 m2/h

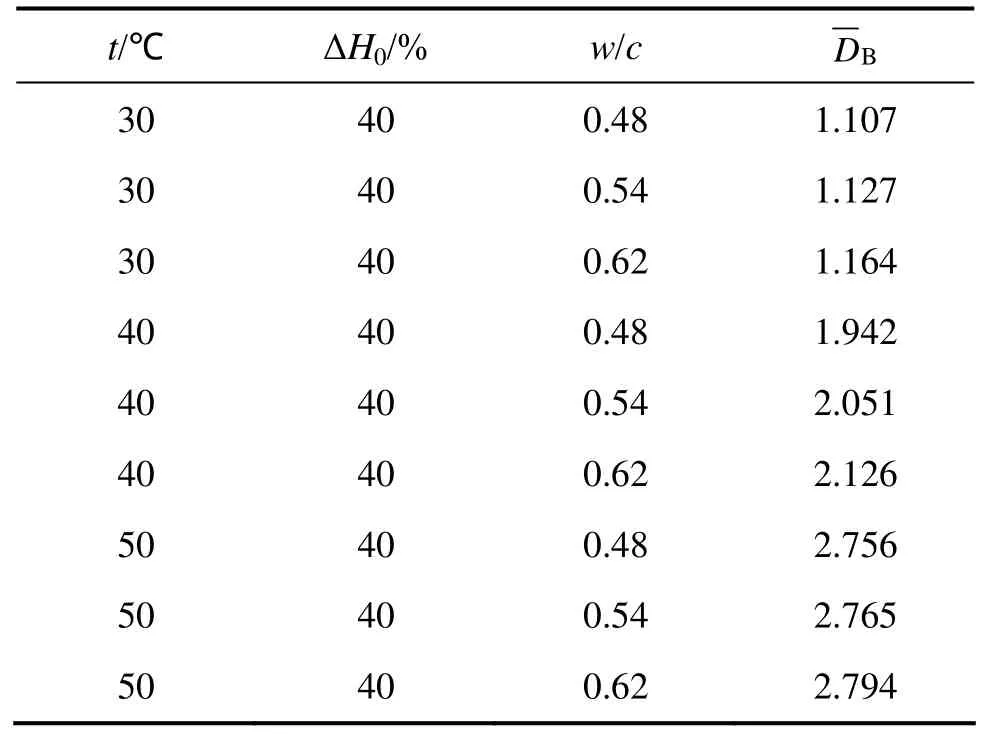
表6 混凝土反向等效湿气扩散系数Table 6 Equivalent backward diffusion coefficients of moisture in concrete 10−6 m2/h

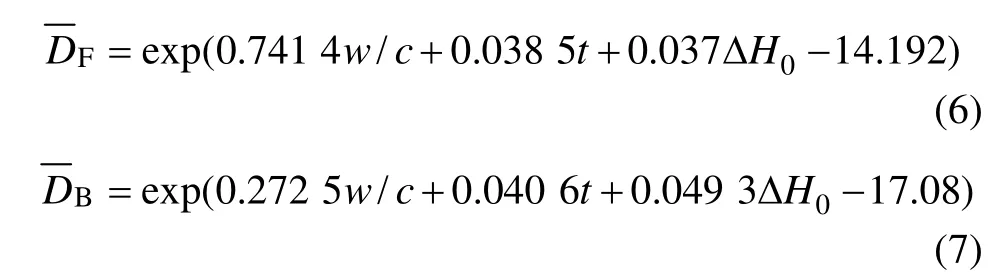
式中：F为混凝土正向等效湿气扩散系数，m2/h；B为混凝土反向等效湿气扩散系数，m2/h；w/c为混凝土水灰比，其适用范围 0.48≤w/c≤0.62；t为混凝土内温度，℃；ΔH0为混凝土内外初始相对湿度差，%。

5 混凝土内相对湿度响应预测模型

5.1 模型的推导

混凝土内的湿气传输过程由 Fick第二定律所决定[14]：

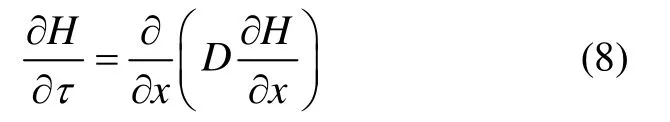
式中：H为相对湿度，%；D为混凝土的湿气扩散系数， m2/h；τ为时间，h。

混凝土内相对湿度响应过程中，D为变值，但根据本文提出的混凝土“等效湿气扩散系数”概念，可以用取代D。于是，式(8)可转化为

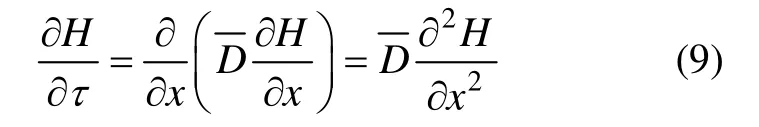
假定混凝土内部初始相对湿度均匀一致为H0，环境相对湿度恒定为He，那么有

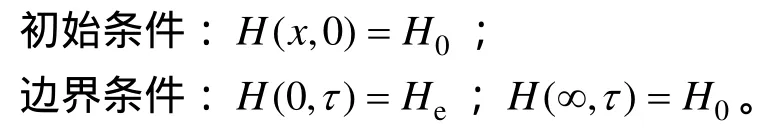
利用初始条件和边界条件对式(9)求解，则可以获得任意时间混凝土内部任意位置处的相对湿度H，如式(10)所示：

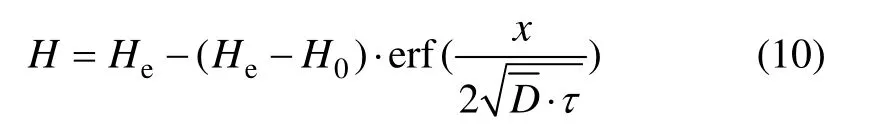
式中：erf(φ)为误差函数；x为距离混凝土表面的深度，m；为湿气在混凝土内的等效扩散系数，m2/h。

5.2 模型的试验验证

混凝土相对湿度响应预测模型式(10)中，涉及误差函数 erf(φ)的计算，本文采用双曲正切函数近似计算法[16]，即

下面以试验 HR-F-1为例，介绍混凝土内相对湿度响应值的计算过程。已知条件为：测试点距混凝土表面的距离x=0.025 m，混凝土水灰比w/c=0.54，温度T=30 ℃，实际混凝土内初始相对湿度H0=65.7%，实际环境相对湿度He=74%。

(1) 首先，利用公式(6)计算相应的混凝土等效湿气扩散系数：

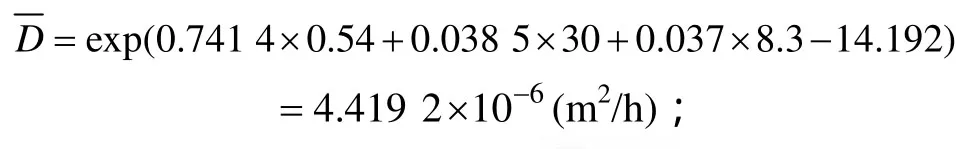
(2) 将等效湿气扩散系数代入式(11)，计算得到对应不同时刻的误差函数值erf(φ)；

(3) 将混凝土内初始相对湿度H0，环境相对湿度He，以及不同时刻的误差函数值erf(φ)代入式(10)，计算得到对应不同时刻的混凝土内相对湿度响应值。将混凝土内相对湿度的计算值与实测值比较，结果如图8所示。

同理，可以计算反向响应试验 HR-B-2中混凝土内相对湿度响应结果，如图9所示。

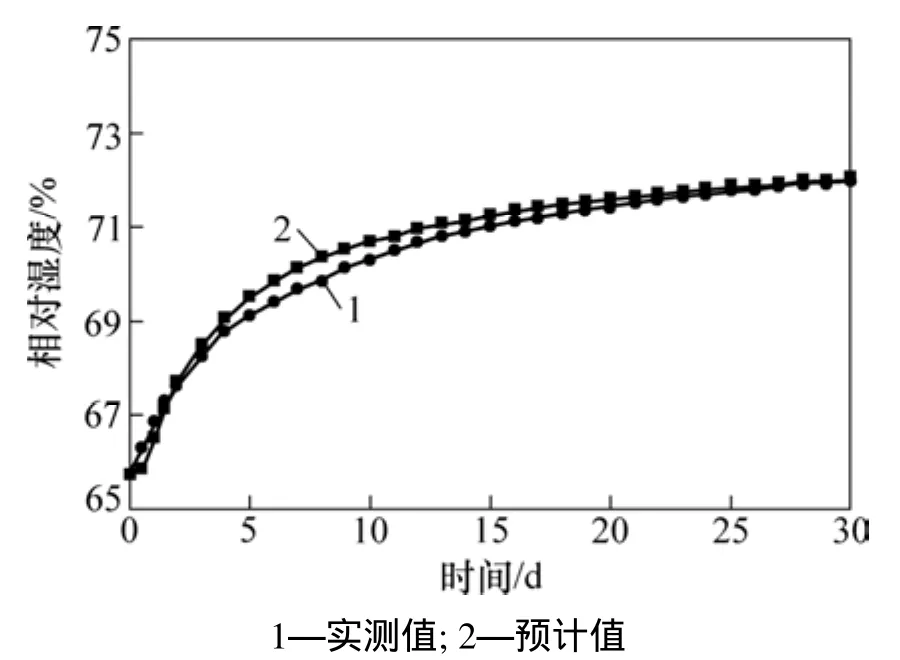
图8 试验HR-F-1中混凝土相对湿度计算值Fig. 8 Calculated values of relative humidity in concrete during test HR-F-1

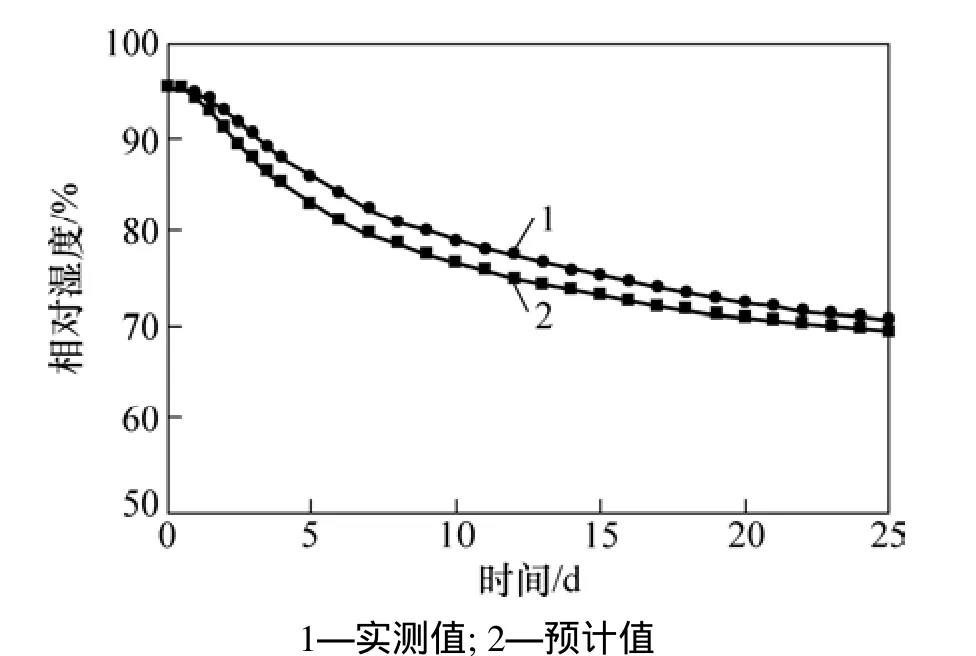
图9 试验HR-B-2中混凝土相对湿度计算值Fig. 9 Calculated values of relative humidity in concrete during test HR-B-2

从图8和图9中可以看出：混凝土内相对湿度的理论计算值与实测值变化趋势一致，并且数值上较吻合。分析其原因，主要是由于本文的混凝土等效湿气扩散系数计算模型，综合考虑了混凝土水灰比、温度和初始湿度差的影响；同时，通过改进混凝土内相对湿度的测量方法，提高了试验数据的精度。验证结果表明：本文建立的混凝土等效湿气扩散系数计算模型与混凝土内相对湿度响应预测模型可行。

6 结论

(1) 人工气候环境下，混凝土内相对湿度与环境相对湿度响应存在显著滞后。混凝土水灰比w/c、温度T和初始湿度差ΔH0是混凝土内相对湿度响应的重要影响因素；w/c越大、t越高、ΔH0越大，相对湿度响应越快。

(2) 混凝土湿气扩散系数是混凝土内相对湿度的函数，同时还受混凝土水灰比、温度和初始湿度差影响；环境风速对混凝土反向湿气扩散系数具有重要影响，且其影响服从指数函数规律。

(3) 基于混凝土湿气扩散系数的变化，本文提出了混凝土等效湿气扩散系数的概念，并建立了综合考虑混凝土水灰比、温度和初始湿度差影响的等效湿气扩散系数计算模型。

(4) 基于混凝土等效湿气扩散系数，利用Fick第二定律建立了恒定人工气候环境下混凝土内相对湿度响应预测模型，并验证了模型的可行性。

[1]Oh B H, Jang S Y. Effects of material and environmental parameters on chloride penetration profiles in concrete structures[J]. Cement and Concrete Research, 2007, 37(1):47−53.

[2]Andrade C, Sarria J, Alonso C. Relative humidity in the interior of concrete exposed to natural and artificial weathering[J].Cement and Concrete Research, 1999, 29(8): 1249−1259.

[3]边松华, 朋改非, 赵章力, 等. 含湿量和纤维对高性能混凝土高温性能的影响[J]. 建筑材料学报, 2005, 8(3): 321−327.BIAN Songhua, PENG Gaifei, ZHAO Zhangli, et al. Effects of moisture contents and fibers on properties of high performance concrete at high temperatures[J]. Journal of Building Materials,2005, 8(3): 321−327.

[4]李魁山, 张旭, 韩星, 等. 建筑材料水蒸气渗透系数实验研究[J]. 建筑材料学报, 2009, 12(3): 288−291.LI Kuishan, ZHANG Xu, HAN Xing, et al. Experimental research of water vapor permeability through building materials[J]. Journal of Building Materials, 2009, 12(3):288−291.

[5]黄达海, 刘光廷. 混凝土等温传湿过程的试验研究[J].水利学报, 2002, 33(6): 96−100.HUANG Dahai, LIU Guangting. Experimental study on moisture transfer in concrete under quasi isothermal condition[J].Journal of Hydraulic Engineering, 2002, 33(6): 96−100.

[6]Delgado J M P Q. Measurement of diffusion coefficients in building materials using the initial rate of sorption[J]. Defect and Diffusion Forum, 2006, 258/259/260: 85−90.

[7]Norris A, Saafi M, Romine P. Temperature and moisture monitoring in concrete structures using embedded nanotechnology/micro-electromechanical systems (MEMS)sensors[J]. Construction and Building Materials, 2008,22(2):111−120.

[8]Chang C Y, Hung S S. Implementing RFIC and sensor technology to measure temperature and humidity inside concrete structures[J]. Construction and Building Materials, 2012, 26(1):628−637.

[9]Barroca N, Borges L M, Velez F J, et al. Wireless sensor networks for temperature and humidity monitoring within concrete structures[J]. Construction and Building Materials,2013, 40(3): 1156−1166.

[10]马文彬. 气候环境变化与混凝土内微环境的响应规律研究[D].徐州: 中国矿业大学建筑工程学院, 2007: 62−69.MA Wenbin. Response regularity of microenvironment in concrete under climate variations[D]. Xuzhou: China University of Mining and Technology. School of Architecture and Civil Engineering, 2007: 62−69.

[11]Ryu D W, Ko J W, Noguchi T. Effects of simulated environmental conditions on the internal relative humidity and relative moisture content distribution of exposed concrete[J].Cement and Concrete Composites, 2011, 33(1): 142−153.

[12]Parrott L J. Some effects of cement and curing upon carbonation and reinforcement corrosion in concrete[J]. Materials and Structures, 1996, 29(3): 164−173.

[13]Nilsson L O. Long-term moisture transport in high performance concrete[J]. Materials and Structures, 2002, 35(10): 641−649.

[14]李汝辉. 传质学基础[M]. 北京: 北京航空出版社, 1987:133−169.LI Ruhui. Mass transfer theory[M]. Beijing: Beihang University Press, 1987: 133−169.

[15]孙红萍. 表层混凝土导热系数与湿质扩散系数的规律研究[D].徐州: 中国矿业大学建筑工程学院, 2009: 53−82.SUN Hongping. Study on thermal conductivity and humidity diffusion coefficient of surface layer concrete[D]. Xuzhou:China University of Mining and Technology. School of Architecture and Civil Engineering, 2009: 53−82.

[16]田锦州, 徐乃忠, 李凤明. 误差函数 erf(x)近似计算及其在开采沉陷预计中的应用[J]. 煤矿开采, 2009, 14(2): 33−35.TIAN Jinzhou, XU Naizhong, LI Fengming. Proximate calculation of error function erf(x) and its application in mining subsidence prediction[J]. Coal Mining Technology, 2009, 14(2):33−35.