飞轮储能系统中径向永磁轴承的设计研究
杨乐鑫,周 瑾,张昕烨
(南京航空航天大学机电学院,江苏 南京210016)
0 引言
飞轮储能技术由于轴承摩擦带来的能量损耗阻碍了飞轮技术的更进一步发展。近年来,以铷铁硼(Nd FeB)为代表的稀土永磁材料得到了迅速发展,从而促进了永磁磁悬浮技术的研究。
磁悬浮轴承具有以下优点:无机械接触、无润滑必要、高转速、低噪音,能够有效地减少飞轮转动中轴承上消耗的能量,从而提高飞轮储能效率[1]。永磁轴承与电磁轴承相比,由于没有电子控制系统,具有设计简单装配难度小的特点,能够比较好地精简系统结构、降低设计装配难度,为飞轮技术的开发研究提供便利条件。因此,设计了一种能够应用于飞轮系统的径向永磁轴承,并利用数学模型以及有限元软件研究了其承载能力和特性。
1 飞轮储能系统中径向永磁轴承的结构设计
飞轮储能装置一般由飞轮转子、轴、轴承、电机、真空容器和电力电子装置组成[2]。飞轮转子的放置方式一般有卧式和立式2种。在静态情况下,这2种放置方式皆可应用。在动态场合,为减小基础运动引起的动载荷及陀螺效应,多采用立式放置[3]。
永磁轴承的结构形式有很多。按照永磁轴承的功能来划分,主要可以分为径向永磁轴承和轴向永磁轴承。其中,径向永磁轴承主要可以根据力的类型分为吸力型和斥力型。在实际生产应用中,由于磁环径向磁化的难度相对较大,现在一般主要采用轴向磁化的方式对磁环进行磁化,并利用这种磁环来组建永磁轴承。
另外,单对磁环构成的永磁轴承承载能力相对有限。根据杨伟波等人的研究[4],对永磁轴承进行轴向磁化,在磁环厚度一定、轴向没有偏心和径向有偏心时,磁环所受径向力与磁环叠加的对数近似成线性关系。而与增加单对磁环厚度的方法相比,采用增加磁环对数的方法更加有效。因此,为获得更大的刚度和承载力,经常采用多对磁环进行叠加。
选择2对轴向磁化斥力型磁环叠加作为径向轴承,结构如图1所示。

图1 径向永磁轴承结构
两对永磁磁环分别固定在轴承的内外圈上,由各自的上下压板提供轴向约束。磁环两侧贴上硅钢片,磁通在硅钢片中集中径向流动,从而增加了径向磁通密度,降低了漏磁[5]。
根据谭庆昌等人的研究[6],永磁轴承的承载能力最大的情况出现在内外磁环轴向对齐的情况下,当内外磁环出现1 mm的轴向偏移时,轴承的承载能力下降约25%。因此,考虑到内外轴承实际装配的问题,永磁轴承的设计需要做出一种能够让磁环在实际使用中进行轴向调整的装置。目前,有些轴向调整装置有外加轴向差动调整装置和拉杆调整装置。外加轴向差动调整装置可以对整个系统转子的轴向偏移进行精确地调整,但是其结构复杂、占用空间大,同时由于其是对整个系统转子进行调整,而非对每对轴承进行单独调整,因此,难以使每对轴承都达到理想工作状态。而拉杆调整装置是采用多根拉杆并通过拧动拉动螺母实现轴向位移调整,但在实际使用中,各拉杆难以做到同时进给,因此,调整精度不佳、实用性较低。
由于永磁磁环的工作特性,径向并没有特别高的定位要求,轴向也不会受到较大的力,因此,外环与基座采用自锁螺纹配合。并在外环上压板设计一段圆柱形突出,方便拧动轴承外环,进行轴向调整。这样的设计结构简单、安装与操作方便,可以精确地针对各对永磁轴承单独地进行调整,具有较高的灵活性。同时降低了永磁轴承的装配难度。
2 永磁轴承的数学模型分析
对于径向永磁轴承的数学建模方法主要有5种[7]。即由 Yonnet建立的通用数学模型[8]、简化数学模型[9]、Dellinger在此基础上结合等效磁荷法建立的等效磁荷法假想圆柱形数学模型、谭庆昌等人建立的等效磁荷法径向磁化数学模型[6]、修世超等人建立的等效磁荷法轴向磁化数学模型[10]。
除开通用数学模型误差较大,其余数学模型误差较小[4]。从简化计算的角度出发,选用Yonnet简化数学模型。需要说明的是,孙立军等人证明,这种方法计算出的结果可能比实测值偏小。
Yonnet简化数学模型是将同轴内外磁环作为无限长的条形磁体进行处理,再结合等效磁荷法,根据单位长度两块磁体之间的静磁能、静磁能对坐标X,Y的一次导数和二次导数,建立起轴向磁化的径向永磁轴承的简化数学模型。
磁环尺寸如图2所示,永磁轴承参数为:R4=30 mm;R3=24 mm;R2=22 mm;R1=16 mm;δ=R3-R2=2 mm;d=R2-R1=R4-R3=6 mm;L=5 mm;B=1.3 T。

图2 磁环尺寸
当磁环轴向偏移为0时,径向刚度kr和轴向力Fz的计算公式为:
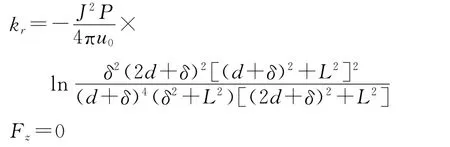
J为内、外环磁化强度。当外磁场为0时,有:

经计算,可得:

根据谭庆昌等人的研究[6],只有当内外磁环的偏心距e接近内外磁环之间的气隙δ的情况下,轴承的承载能力才会和偏心距之间表现出曲线关系,其他情况下,即内外磁环的偏心距e小于内外磁环之间的气隙δ时,轴承承载能力与偏心距e之间基本都呈现出良好的线性关系。即

故当e=1 mm时,Fr=19 N。
3 永磁轴承的有限元分析
目前,永磁轴承的设计理论还并不完善,通常是采用等效磁荷的方法对轴的承载能力进行计算。这一类方法的缺点是忽略了磁环的曲率效应,而把2个磁环的相互作用等效成了2个无限长永磁体的相互作用。同时,利用数学模型进行计算,通常会出现比较复杂的四重积分计算[4]。相对于传统的数学模型计算,有限元分析的方法成为了一种简便、有效的计算方法,尤其是在三维模型的分析上。在此,选用ANSYS Workbench 14.0作为有限元分析软件进行分析。相较于传统的ANSYS Classic和APDL的仿真方式,Workbench的工作方式更加简单直观,同时更有利于与其他CAD软件进行数据共享,具有强大的模型处理能力。
3.1 磁环承载能力分析
将Geometry模块放入项目中,利用Design-Modeler(DM)建立几何模型。DM的操作方式与常见CAD软件相似,易于上手。在建立起磁环后,可以直接利用DM的Enclosure工具生成包围磁环的空气场。划分网格后求解受作用的单元组件即内环所受的合力。根据ANSYS Workbench仿真可知,当内磁环相对于外磁环径向偏移1 mm时,在该方向上内环所受力为20.649 N。这一结果与数学模型计算出的结果相近。
3.2 磁环承载特性研究
利用ANSYS Workbench软件,对磁环的承载特性从磁环厚度、径向偏移量以及轴向偏移量3个方面进行了分析。
3.2.1 磁环承载特性与磁环厚度的关系
选取磁环的内外环径向尺寸和径向偏移量与数学模型计算时相同,轴向无偏移,分别从2~8 mm中,每隔1 mm选取1个尺寸,作为内外磁环厚度进行仿真。计算结果如图3所示。

图3 磁环厚度与径向力关系曲线
由图3可知,在只有径向偏移而无轴向偏移时,随着磁环厚度的增加,径向力也在增加,但其增速明显由快变慢。这符合前文所述,磁环厚度达到一定值后,厚度的增加带来的效果不大。
3.2.2 磁环承载特性与磁环径向偏移量的关系
在磁环没有轴向偏移的情况下,在径向移动磁环,在其径向偏移量不同的情况下进行仿真。得到了如图4所示的结果。

图4 磁环径向偏移与径向力关系曲线
图4 表明,磁环所受的径向力与其径向偏移量基本保持一种线性增加的关系。这说明永磁径向轴承是一种刚性轴承。
3.2.3 磁环轴向偏移量与磁环轴向偏移量的关系
设定内外磁环的径向偏移为1 mm,在轴向移动永磁内环,使其与外环有不同的轴向偏移量并进行有限元仿真。得到了如图5所示的计算结果。

图5 磁环轴向偏移与径向力、轴向力关系曲线
由图5可以看出,随着内外环轴向偏移量的增加,径向力逐渐减小、轴向力快速增大。也就是说,轴向偏移量的增加,会逐渐使永磁轴承从径向工作状态转变到轴向工作状态。因此,内外磁环的轴向偏移是在径向永磁轴承设计时需要避免的。
4 结束语
根据飞轮储能系统的要求,在径向永磁轴承外环采用了螺纹配合,使得轴承内外环能够进行轴向调整,有效地降低了装配难度。通过研究发现磁环径向力随着磁环厚度的增加而增加,但其增速明显由快变慢;而径向力与径向偏移量基本保持一种线性增加的关系;此外,随着内外外环轴向偏移量的增加,径向力逐渐减小、轴向力迅速增大。设计结构简单且便于调节,所述方法简单易行,可用于永磁轴承工程设计与优化。另外,在永磁轴承的实际制作过程中,发现磁环的磁化精度也极大地影响了轴承的工作状态及稳定性。
[1] 汤双清,胡 欢.磁悬浮轴承的应用现状与展望[J].机床与液压,2009,37(12):209-211.
[2] 程三海,韦忠朝,王雪帆.飞轮储能技术及其应用[J].电机电器技术,2000,(6):31-33.
[3] 杨志轶,赵 韩,王 勇,等.飞轮电池磁轴承系统结构及控制[J].合肥工业大学学报(自然科学版),2002,25(6):1107-1111.
[4] 杨伟波,张锦光.基于ANSYS的径向永磁轴承承载特性研究[J].机械设计与制造,2010,(1):146-147.
[5] 陈立志.磁悬浮轴承在高速旋转机械上的应用及一种混合径向磁悬浮轴承的设计[J].光学精密工程,1994,2(4):101-108.
[6] 谭庆昌,刘明洁,孟慧琴,等.永磁向心轴承承载能力与刚度的计算[J].摩擦学学报,1994,14(4):337-344.
[7] 孙立军,张 涛,赵 兵.永磁磁轴承数学模型的研究[J].机械工程学报,2005,41(4):69-74.
[8] Yonnet J P.Permanent magnet bearings and couplings[J].IEEE Transactions on Magnetics,1981,17(1):1169-1173.
[9] Yonnet J P,Hemmerlin S,Rulliere E,et al.Analytical calculation of permanent magnet couplings[J].IEEE Transactions on Magnetics,1993,29(6):2932-2934.
[10] 修世超,谭庆昌,孟慧琴.同轴环形磁铁磁作用力计算的等效磁荷法[J].沈阳黄金学院学报,1995,14(3):359-363.

