基于粒子滤波的电力机车电气故障诊断

王亚亮，衣法臻，王忠立

（北京交通大学 电子信息工程学院，北京 100044）

列车故障诊断就是对列车运行现状的诊断，也是对运行趋势的一种预测。如图1所示，列车故障诊断主要分为3部分，分别为：机械部分、电气部分和空气管部分。其中，电气系统故障诊断在列车故障诊断中占据非常重要的一部分，对于电力机车更是如此，因为电力机车的电气部件复杂、数量多、检测条件差。如图1所示，电气系统故障诊断主要包括对8个子系统的故障诊断[1]。为了监测每个子系统的工作是否正常，需要安装多个传感器对各个子系统中的多个性能指标进行检测并判断其是否满足要求。随着电气系统越来越复杂，电气部件越来越多，需要检测的局部电气指标越来越多，所需要的传感器数目也越来越多。如果继续按传统的方式把传感器检测的信息不加处理的传给故障诊断中心并由其进行数据融合和决策，一方面大量的检测数据会增加通信的压力，另一方面诊断中心需要实时地处理由传感器检测的大量数据，这无疑会对诊断中心的实时性能造成重大影响，如果数据处理不及时可能会引起诊断系统的瘫痪，甚至发生车毁人亡的现象。为了解决这个问题，故障诊断系统采用分布式传感器网络（Distributed Sensor Network，DSN）实现对传感器检测数据进行实时处理（决策）。DSN最大的优点是每个传感器都可独立处理自身的信息。虽然对单一结构的系统或设备故障诊断的研究已经进行了很多年，也有很多可喜的成果[2～6]，但是，采用DNS对系统的故障信息融合决策和预测、预警方面的研究国内外可以借鉴的文章并不多。近年来由于系统智能化发展的需求，DSN发展迅速，在很多系统中均采用这种结构类型，尤其是在传感器数量比较多的情况下，如：列车电气故障诊断系统。所以，研究分布式故障诊断方法，对列车电气系统的正常工作、故障安全以及列车安全、高效运行都至关重要。

图1 基于TCN的电力机车电气故障诊断系统

在列车电气部件工作时，分布式故障数据是动态变化的，各个数据之间有着复杂的关系，而且这种关系不容易用现有的数学理论进行表述，另外，各系统输入不是相互独立的，也是有相互关系，这些原因共同导致在分布式系统中寻找最优决策困难重重。可以利用多个传感器合理、有效地分工协作来解决寻找最优策略困难的问题，在基于这点的基础上，获得各个传感器的检测值，经过二值决策将结果传送到信息融合中心进行数据融合和最终决策，实现了列车电气系统诊断和预警功能。由于实际系统一般都不是线性系统或高斯系统，为了简化讨论的复杂度和计算量，本文所有的研究都是在各系统状态独立分布的基础上进行的，由于系统状态独立，传感器获得的系统状态检测数据也是相互独立的，这种假设在大多数实际应用中是比较合理的。

1 电气故障诊断系统描述

假设系统正常状态为S0，故障状态为S1，动态系统满足马尔科夫性质[7]，即满足：p(xk|xk-1,xk-2, …x0)=p(xk|xk-1)（系统在某一时刻的状态只与前一时刻的状态有关，其中，p(xk|xk-1)为k－1时刻到K时刻的状态转移概率密度函数）。假设有m个相同传感器检测被诊断系统，根据动态空间模型理论[8]，动态系统的状态变量方程和量测方程为：

其中，e=0,1分别表示正常和故障两种情形，vk∈Rnv为过程噪声，∈Rnv为第 个传感器的量测噪声，l=1, 2, …, m 。

图2为故障诊断系统框图。

图2 故障诊断系统框图

根据图2中所示，各个传感器通过检测每个分布系统的状态，将获得的数据经过局部检测器分别进行二值决策，信息融合中心将收到的二值决策结果进行融合、全局决策得出故障检测结果。由于从各个局部检测器到信息融合中心通信所传输的数据仅为二值信息，减少了通信量，也降低了信息融合中心的计算量，提高了故障诊断的效率，给故障实时报警提供了可能性。其中，局部检测器是判断系统局部是否发生故障，其数学表达式如下：

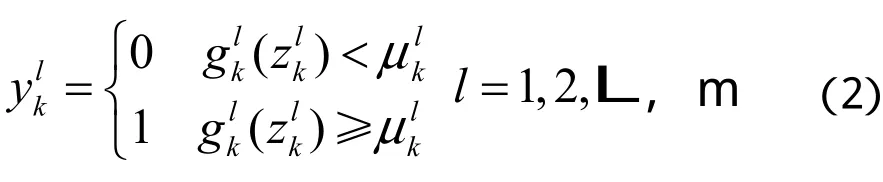
其中，Tk是统计函数，负责统计时刻k所有的局部故障信息，tk是时刻k系统故障决策阈值。yk表示时刻k系统故障决策结果，0表示系统正常工作，1表示系统处于故障状态。

如果判断系统处于故障状态，系统会做出相应的响应，如发出声光报警、电气隔离、故障导向安全等。如果判断系统正常工作，则应该更新各个局部后验概率密度函数。（1）式决定了整个诊断系统性能的优劣，所以对这两个决策表达式寻优就成为本文的研究重点，基于贝叶斯基本理论的最小方差概率估计法经过验证满足要求。在最小方差概率方法中，系统估计和预测的有效性，对非线性、非高斯系统是否适用都决定着局部和最终决策的性能，从而决定诊断系统的性能。粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法，适用于任何能用状态空间模型表示的非高斯背景的非线性随机系统，适用于诊断系统的局部决策和信息融合决策。

2 诊断系统算法设计

2.1 算法设计

假设系统在S0和S1两种情形下状态转移概率密度函数分别为p0(xk|xk-1)和p1(xk|xk-1)，k时刻第 l个状态的先验概率密度函数为p(xk|zl1∶k-1)，后验概率密度函数为各个传感器获得系统各个状态的实时观测数据，粒子滤波器分别在S0和S1两种情形下根据观测数据进行状态预估和更新。根据贝叶斯理论[9]和SIS（序贯蒙特卡罗采样法）对后验概率密度函数进行采样，获得采样粒子，则后验概率可以表示为下式[10～12]。

其中，N为粒子总数，ωik为粒子i 的权值，重要性函数，可用p(xk|xk-1)代替。

为了简化模型，假设传感器的测量数据独立同分布，那么各传感器在正常和故障两种情形下的观测概率密度函数可以用下式表示。

其中，e=0,1分别表示正常和故障两种情形。为了使误差概率最小化，采用局部似然率的方法对局部决策和阈值取优，假设各个传感器决策规则相同，μlk是局部决策的阈值，局部决策对应的积分区域为Rlzk，那么局部正常与故障的概率可以通过分别对pl0(z)和pl1(z)在区域Rlzk内求积分获得。

当各个局部检测的正常和故障概率都相同时，最终决策就是最优的，而且随着传感器数量的增多，这种最优就越明显。最终决策函数其实是一个统计函数，在S0和S1两种情形下，统计分别满足二项式分布(m, plk(0))和(m, plk(1))。当传感器数目很多时，可以用De Moivre-Laplace表示统计概率，融合决策的误差概率表达式如下。

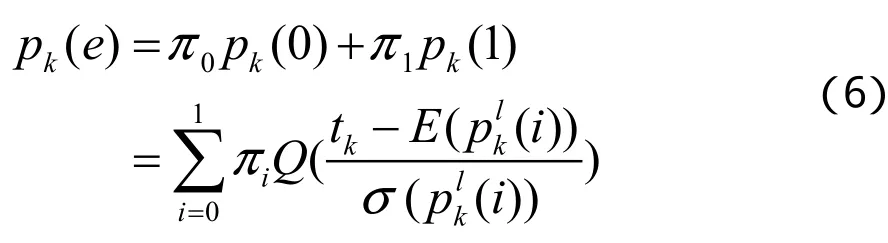
其中，π0和π1分别为S0和S1两种情形下的先验概率，pk(0)和pk(1)分别是两种情形下的统计概论，函数Q(g)是标准高斯函数的互补分布函数，E(plk(0))为随机变量plk(0)的均值，σ(plk(0))为随机变量的标准差。分析上式，我们得出如下结论：改变局部决策阈值和融合决策阈值可以改变pk(0)和pk(1)，从而影响最终的误差概率，为了使误差概率尽量小，需要对局部决策阈值和融合决策阈值求最优解，局部决策阈值与pk(0)有对应关系，于是问题就转化为在满足0≤tk≤m和0≤pk(0)≤1条件下使误差概率最小化的二值优化问题。采样NM单纯形法不仅能够求得最优解，实时性能也很优异，最终，结合对数似然法，将局部决策函数变形为下式。

其中，μlk,opt为局部决策阈值，可以用k－1时刻的粒子联合表示，同时，融合决策表达式如下。

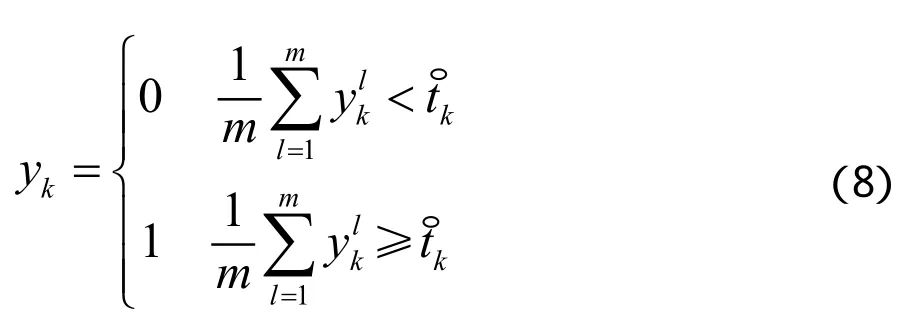
2.2 算法流程

步骤1：对m个传感器分别执行以下子步骤。

（1）根据式（5）估计观测概率；

（2）根据k－1时刻的粒子联合表示μlk,opt和

（3）根据式（7）计算 ylk。

步骤3：根据式（8）计算yk。

步骤4：如果yk为0，根据式（4）更新后验概率和权值；否则，输出预警信息并停止诊断系统。

3 诊断系统仿真结果

实验所用的状态空间方程为：

其中，vk为过程噪声，在S0和S1情形下分别满足N(0, Q0)和N(0, Q1)，nlk为第l个传感器的量测噪声，l=1, 2, L m，满足 。图3是tk的均方误差随粒子数的变化函数，从图3中可以看出随着粒子数目的增多，tk的均方误差逐渐减小，最终稳定在0附近。

图3 均方误差仿真结果

图5 是误差概率随传感器数目变化的函数，粒子数目取150，当传感器数目足够多时误差概率趋于稳定，这时的误差主要是由观测噪声、状态噪声和各传感器之间不完全独立造成的。

图4 误差概率仿真结果

4 结束语

本文采用DSN对列车电气系统进行故障诊断仿真研究，采用适用于非线性、非高斯分布系统的粒子滤波对后验概率进行估计、采样和更新，局部决策函数将每个传感器检测、估计的系统状态信息与局部决策阈值比较，输出局部决策二值信息，融合决策中心将各个局部决策输出的二值信息进行融合并与融合阈值比较，输出最终决策信息，如果诊断电气系统故障，则进行故障报警，否则，继续更新先验概率和后验概率，并对观测状态进行预测。仿真结果证明诊断系统的性能与粒子数、传感器数目、各传感器检测数据之间的相关性等有直接关系，另外，实验结果验证了粒子滤波在诊断系统中的有效性。

[1]黄采伦，樊晓平，陈特放．列车故障在线诊断技术及应用[M]．北京：国防工业出版社，2006．

[2]A.Willsky. A survey of design methods for failure detection in dynamic systems[J]. Automatica, Vol. 12, pp.601-611, 1976.

[3]C. M.Belcastro and B.Weinstein. Distributed detection with data fusion for malfunction detection and isolation in fault tolerant flight control computers[C]. Proceedings of the American Control Conference, Anchorage, AK, May 2002.

[4]A. Doucet, Nando de Freitas, N. Gordon (eds). Sequential Monte Carlo Methods in Practice[M]. New york: Springer-Verlag,2001.

[5]C. Andrieu, A. Doucet, S. Singh, V. Tadic. Partticle methods for change detection, system identification and control[C].Proceedings of the IEEE, Vol. 92, No.3, pp. 423-438,Mar.2004.

[6]Q. Zhang, P. K. Varshney, R. D. Wesel. Optimal bi-level quantization ofi.i.d. sensor observations for binary hypohesis testing[C]. IEEE Trans. Inform. Theory, Vol. 48, No. 7, pp. 2105-2111,July 2002.

[7]A. Doucet, N. de Freitas, N. Gordon. An introduction to Sequential Monte Carlo methods. in Sequential Monte Carlo Methods in Practice[M]. New York : Springer-Verlag, 2001.

[8]朱志宇.粒子滤波算法及其应用[M].北京：科学出版社，2010.

[9]胡士强,敬忠良.粒子滤波原理及其应用[M].北京：科学出版社，2010.

[10]D.Crisan, A.Doucet. A survey of convergence results on particle filtering methods for practitioners[C]. IEEE Trans. On Signal Processing, Vol. 50, No.3, pp. 736-746, Mar. 2002.

[11]N. de Freitas. Rao-Blackwellised Particle Filtering for Fault Diagnosis[C]. in IEEE Aero space , 2002.

[12]V. Kadirkamanathan, P. Li , M. H. Jaward, S.G. Fabri, Paticle filtering-based fault detection in non-linear stochastic systems[J]. International Journal of Systems Science, vol. 33,no. 4, pp. 259–265, 2002.