太阳帆航天器姿态机动的复合控制研究

翟 坤 张 瑾 王天舒

（清华大学航天航空学院，北京100084）

1 引言

太阳帆航天器（简称太阳帆）是一种直接利用太阳光子在高反射薄膜表面反射产生推力的新型航天器[1]。无需携带大量推进剂，就可实现太阳系的深空探测和星际航行任务。

太阳帆在进行深空探测和星际航行等任务过程中，根据任务需不断进行姿态机动，调整太阳帆与太阳光线的夹角，以获得合适的推力。太阳帆具有大柔性空间结构，姿态机动将激起太阳帆的柔性振动，产生影响姿态机动的耦合力矩。而不同于一般的柔性航天器，太阳帆航天器没有质量占优的中心刚体，柔性振动还会造成太阳帆出现严重变形，使转动惯量等结构参数发生剧烈变化，改变太阳帆的动力学特性；同时变形还会造成太阳帆受力不均，产生额外的干扰力矩。而由于太阳帆的振动频率很低，从时间尺度上来看，柔性变形相对姿态机动不再是快周期变化，导致转动惯量的变化和产生的额外干扰力矩均无法忽略，将严重地影响姿态机动过程，甚至造成太阳帆失稳。因此，相对一般柔性航天器，柔性振动对太阳帆姿态机动的影响更加严重。

可用于太阳帆姿态机动的控制手段很多，有安装于太阳帆中心的动量轮和喷气等，还有安装于太阳帆支撑杆顶端的电推进和控制叶片等。最初很多文献采用这些姿态控制手段，在忽略了太阳帆柔性振动的情况下，研究了太阳帆的姿态控制问题[2-4]。近年来，随着太阳帆刚柔耦合动力学建模研究的进行[5-7]，考虑柔性振动的太阳帆姿态控制研究相应地陆续出现[8-11]。文献[10]采用控制叶片研究了柔性太阳帆的姿态机动控制，设计了太阳帆俯仰轴的比例-微分控制器，并指出通过控制叶片的往复摆动可以对太阳帆的柔性振动起到一定的抑制作用，但这种抑制作用是一种被动的柔性振动控制。文献[11]采用输入成型方法研究了太阳帆的开环姿态机动，该方法只能消除姿态机动后的柔性振动，但不能消除姿态机动过程中的柔性振动，无法避免姿态机动过程中转动惯量的变化，具有一定的局限性。

相比一般的姿态机动控制，本文采用两种控制手段（作用于太阳帆中心的喷气和作用于支撑杆顶端的电推进）的组合进行太阳帆的姿态机动，并据此设计复合控制方法，不但实现太阳帆的快速姿态机动，还能消除太阳帆姿态机动过程中的柔性振动，减小柔性变形产生的耦合力矩和转动惯量变化等对姿态机动过程的影响，提高太阳帆姿态机动的精度。

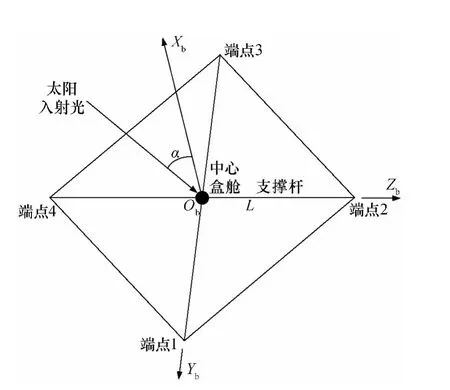
图1 方形太阳帆Fig.1 Square solar sail

2 太阳帆航天器动力学建模

2.1 系统描述

本文研究的方形太阳帆如图1所示，包括4块三角帆膜和4根支撑杆，每块三角帆膜的3个角分别连结到2根支撑杆顶端和中心盒舱。

定义太阳帆本体坐标系ObXbYbZb，其中原点Ob位于太阳帆质心，ObXb沿着太阳帆的法线方向，ObYb和ObZb分别沿着支撑杆的轴向。

首先进行如下假设：

1）参考文献[5，12]的分析结果，忽略帆面与支撑杆的动力学作用，并将帆面质量均匀等效到4根支撑杆上；

2）只考虑太阳帆进行单轴机动，不失一般性，假设太阳帆绕ObZb轴机动。

经过上述假设后，太阳帆可简化为如图2所示的悬臂梁结构。

图2中ωb为太阳帆的转动角速度；L为支撑杆长；ρ为线密度；ma＝ρL为支撑杆质量；EJ为抗弯刚度；ua（y，t）为弯曲变形。Pa为安装在支撑杆顶端的电推进产生的推力。

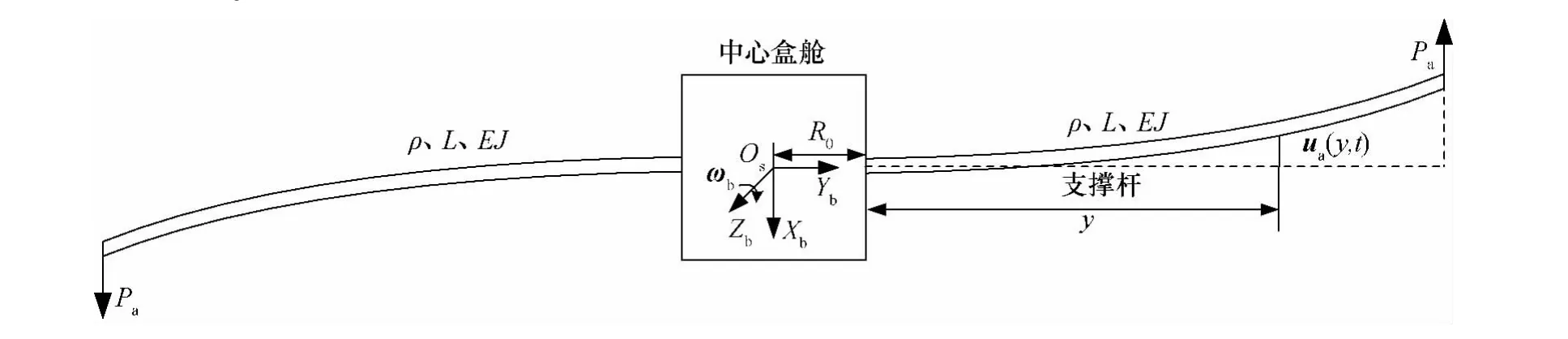
图2 简化太阳帆航天器模型Fig.2 Model of simplified solar sail spacecraft

2.2 动力学方程

应用拉格朗日建模原理，可得太阳帆的动力学方程[13]如下：

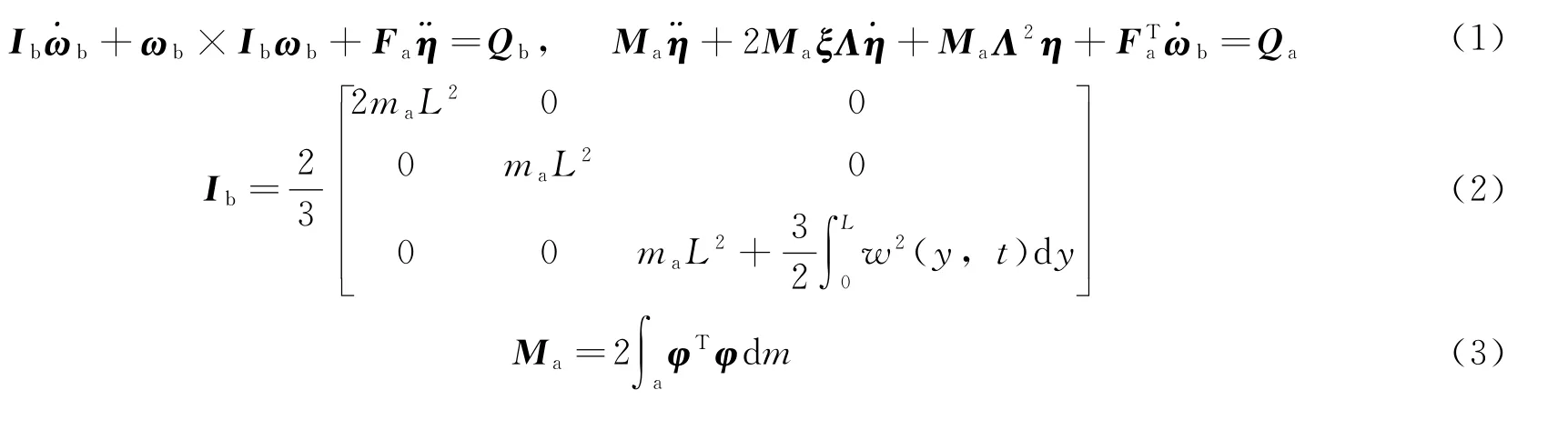
式中 Ib为太阳帆相对本体坐标系的转动惯量；Ma为支撑杆质量矩阵；Fa为支撑杆振动与姿态转动的耦合系数阵；Qb和Qa分别为作用于姿态转动和柔性振动的广义力；Λ为支撑杆振动固有频率对角阵。ξ为支撑杆振动阻尼对角阵；为1×n维的模态振型；η为n×1维模态坐标列阵，n为模态阶数；w（y，t）为支撑杆的横向变形，通过模态离散可得：

选择如下的模态振型：

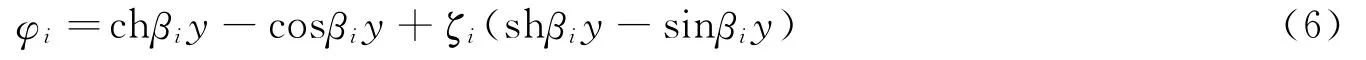
3 复合控制方法

下面详细说明复合控制方法的设计过程，既保证太阳帆的快速姿态机动，还要消除姿态机动过程中的柔性振动，提高太阳帆姿态机动精度。

3.1 动力学方程的变形

在提出复合控制方法前，首先对式（1）进行整理变形。

如果只研究太阳帆绕单轴的姿态机动，可得：ωb×Ibωb＝0。

由模态振型的正交性，可得广义质量

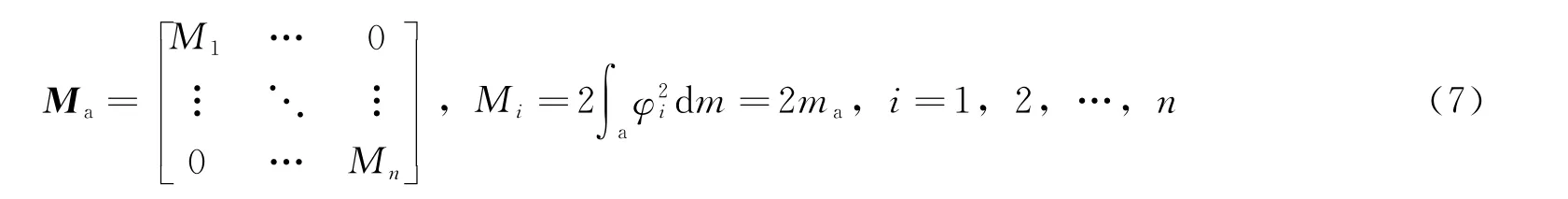
进而可将柔性振动的动力学方程变形为

3.2 复合控制方法

在初始振动为0时，如果使U为0，则姿态机动过程中太阳帆将不会振动。由此出发，下面设计复合控制方法。

首先取喷气产生的控制力矩为Qb1，电推进产生的推力为Pa，则

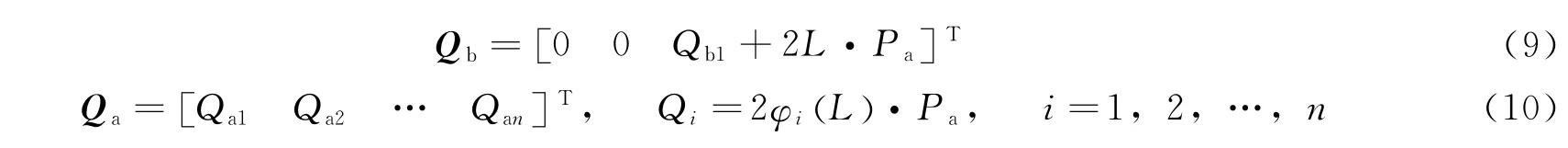
将式（6）代入式（4），则耦合系数阵可表示为

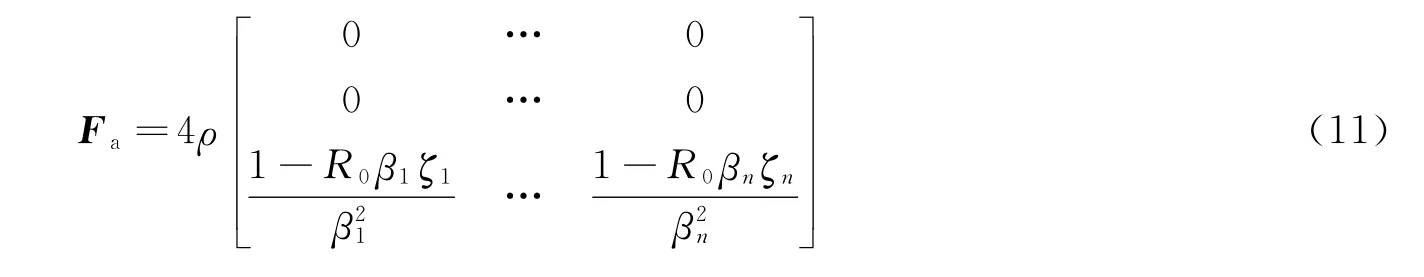
令

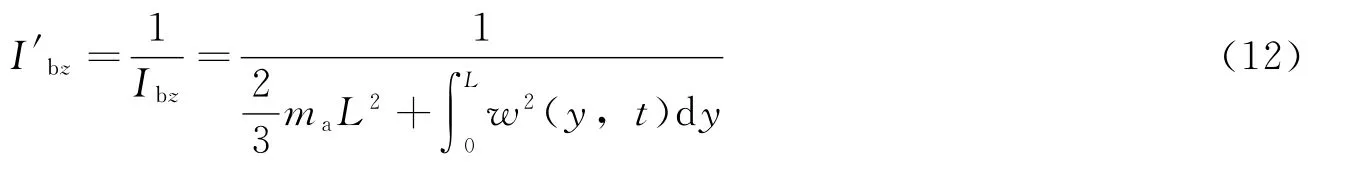
联合式（9）～式（12），可得

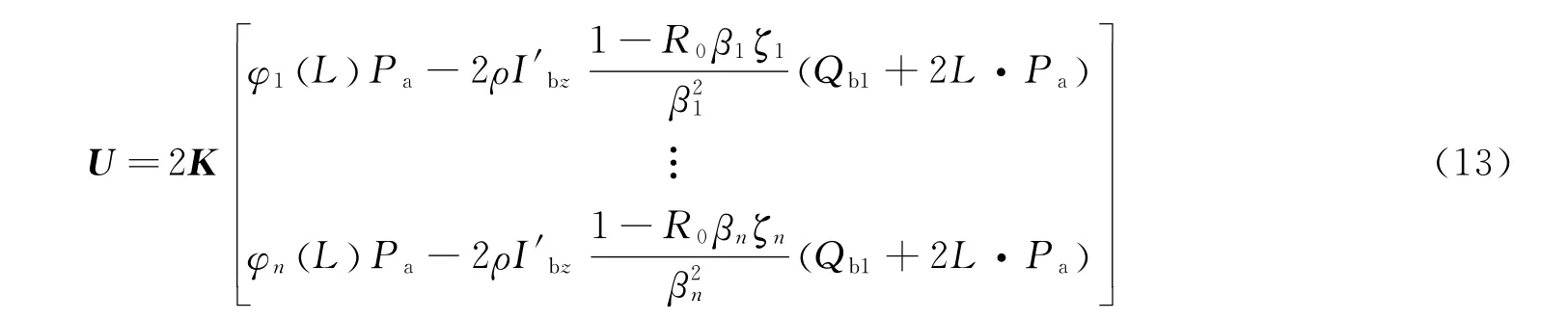
由式（13）可以得到如下2种复合控制方法：

（1）消除某一阶的柔性振动

使该阶振动模态的外加激励为0。以消除第j阶柔性振动为例，有

式中U（j）为向量U的第j个分量。

实际中根据机动角度和机动时间的要求，常选择确定的姿态机动力矩Qbz，即

将式（15）代入式（13）得到

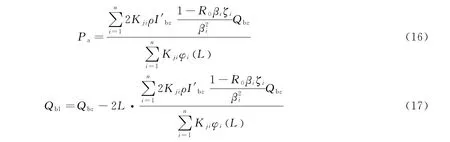
（2）减小前n（n＞1）阶的柔性振动

由式（13）可知，当n＞1时，U＝0没有非0解。为此定义如下性能指标：

式中E为机动过程中的前n阶振动模态坐标平方和的积分，是柔性振动强弱的一种度量；Tm为机动时间。

当E取极小时，可得减小前n阶柔性振动的最优控制输出Qb1和Pa。

从设计思路上，复合控制方法（1）没有考虑振动动力学方程的耦合特性；而复合控制方法（2）是基于多阶模态的综合作用得到的，即考虑了多阶模态的耦合特性，因此复合控制方法（2）的柔性振动抑制效果要比复合控制方法（1）好。

实际上，本文给出的复合控制方法是在考虑消除柔性振动情况下的两种控制手段的控制输出分配策略。通常柔性振动的低阶模态对姿态机动影响较大，因此采用复合控制方法（1）和（2）设计得到的Qb1和Pa，可有效消除太阳帆机动过程中的柔性振动影响。

4 仿真分析

仿真采用的太阳帆参数如表1所示。

假设开环姿态机动角度θm＝30°，选择姿态机动力矩Qbz＝10Nm，并应用Bang-Bang控制策略设计姿态机动指令，即

假设模态坐标及其导数的初值均为0，初始姿态角和角速度均为0，首先进行如下两个工况的仿真：

1）工况1：控制力矩作用于太阳帆中心，针对第一阶模态设计输入成型器[11]（如式 （20）所示），采用输入成型器＋Bang-Bang的控制策略设计姿态机动指令；

2）工况2：针对第一阶模态采用复合控制方法（1）＋Bang-Bang的控制策略设计姿态机动过程，得到控制输出：Qb1＝0.350 5Nm，Pa＝0.068 2N。仿真结果如图3～图6所示。

表1 太阳帆参数Tab.1 Parameters of solar sail

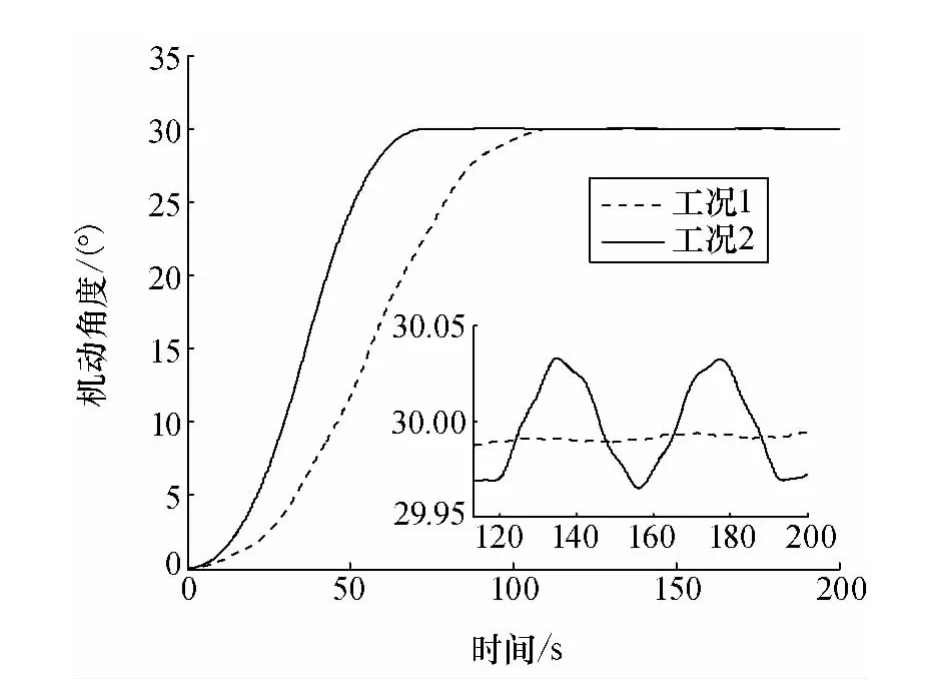
图3 机动角度Fig.3 Maneuvering angles

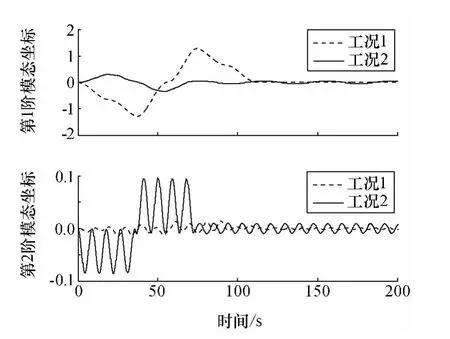
图4 模态坐标Fig.4 Coordinates of modes

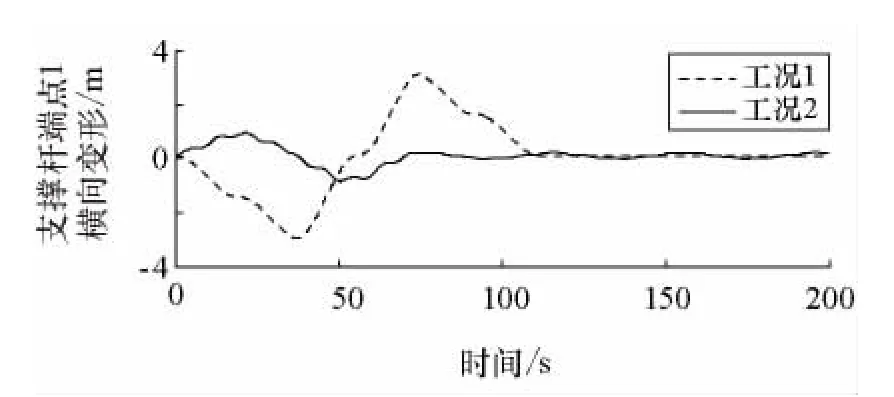
图5 支撑杆端点1的横向变形Fig.5 Transverse distortions of boom′s tip1

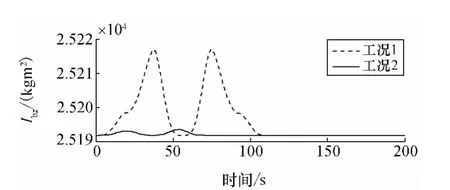
图6 转动惯量ⅠbzFig.6 Moments of inertia Ⅰbz

由图4和图5可知，采用输入成型法使姿态机动结束后的第一阶振动模态得到了消除，但姿态机动过程中仍存在一定的柔性振动，其中支撑杆端点1处的最大横向变形达到了3m。从而由图6可以看出，姿态机动过程中残留的振动变形造成转动惯量出现0.1%的变化，导致图3中的姿态机动稳定后的角度出现0.01°的常值偏差。

而采用复合控制方法（1）不但可以消除姿态机动结束后的第一阶模态，还减小了姿态机动过程中的第一阶模态，使支撑杆端点1处的最大横向变形仅为0.7m，机动过程中的转动惯量变化仅为0.01%，保证姿态机动稳定后的角度无常值偏差，且机动时间较输入成型法短39.58s（也就是输入成型法引入的延迟时间）。

但由图3可知，采用复合控制方法（1）进行姿态机动，稳定后的姿态仍存在0.04°的角度振动。同时我们发现，虽然采用复合控制方法（1）后第一阶振动模态的外加激励为0，但由于动力学方程中第二阶模态的耦合作用，第一阶模态仍存在一定振动。为进一步消除柔性振动影响，下面采用复合控制方法（2）进行姿态机动控制。

3）工况3：根据工况2得到的控制力Pa＝0.068 2N，采用蒙特卡罗仿真求解减小前2阶柔性振动的最优控制输出Qb1和Pa。选择的打靶点为：Pa＝0.02，0.03，0.04，0.05，0.06，0.07，0.08，0.09，0.10，0.11。得到如图7所示的仿真结果。

对蒙特卡罗仿真结果进行线性二次拟合，求得最优的控制输出为：Qb1＝1.316 7Nm，Pa＝0.061 4N。

采用最优控制输出，得到如图8～图11的姿态机动仿真结果。

由图8～图11的仿真结果可知，采用复合控制方法（2）可使第一阶振动模态有进一步的减小，进而使姿态机动过程中的柔性振动得到了进一步的抑制，支撑杆端点1处的最大横向变形仅为0.15m，而姿态精度优于0.003°，且机动过程中转动惯量基本不变。

但由图9发现第二阶振动模态较采用复合控制方法（1）时没有明显的减小。原因在于复合控制方法（2）是根据性能指标E取极小得到的，而由于振动动力学方程的耦合特性（式（8）中K不是对角阵），所以有图9的结果。

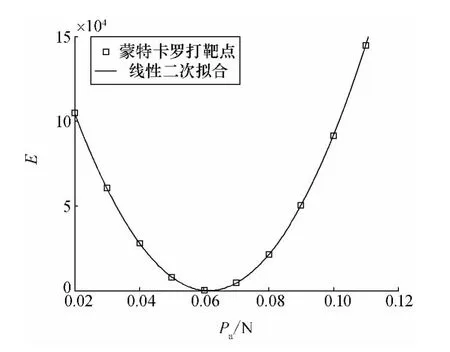
图7 蒙特卡罗仿真结果Fig.7 Results of Monte Carlo simulation

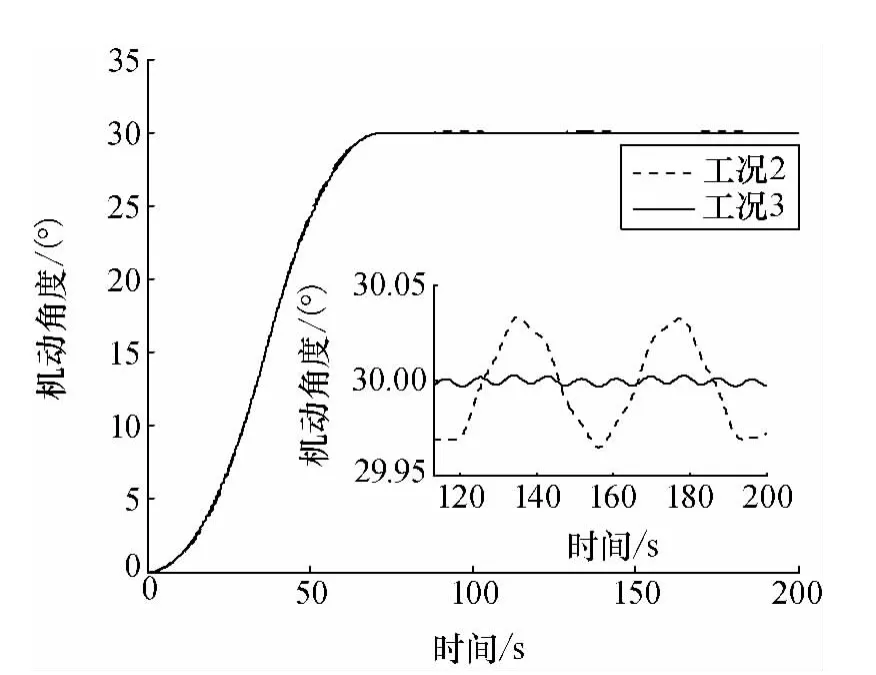
图8 机动角度Fig.8 Maneuvering angles

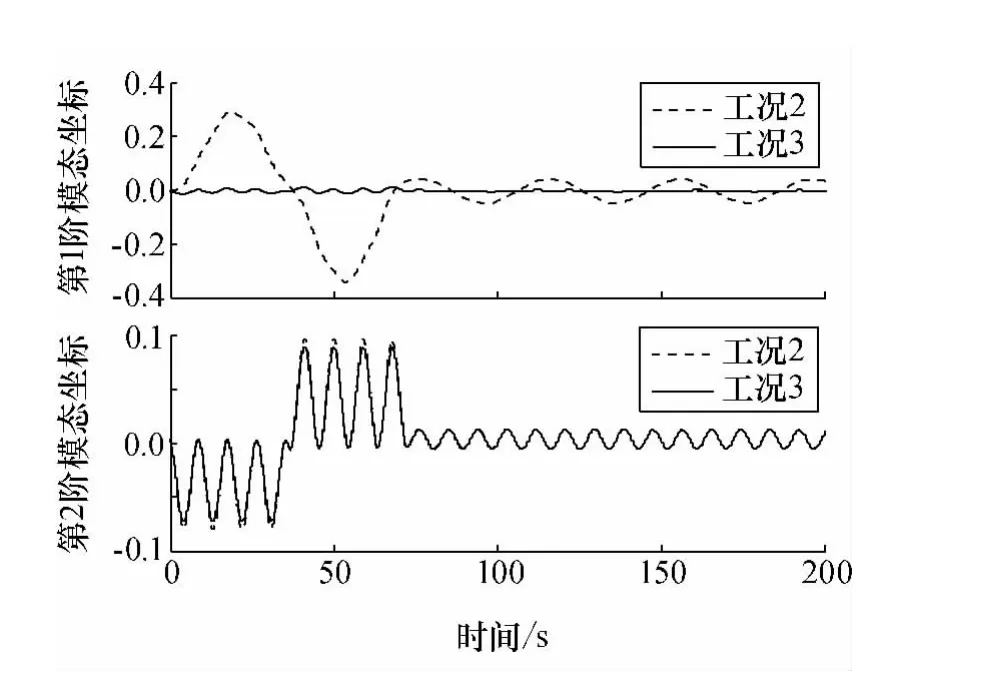
图9 模态坐标Fig.9 Coordinates of modes

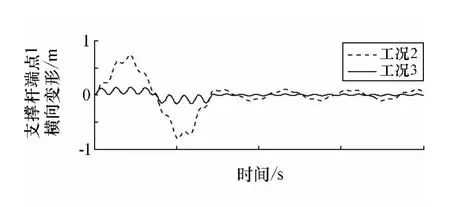
图10 支撑杆端点1的横向变形Fig.10 Transverse distortions of boom′s tip1

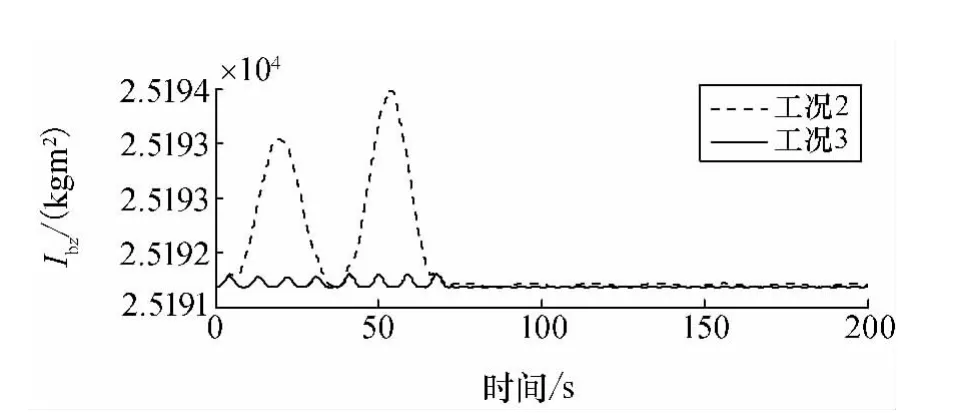
图11 转动惯量分量ⅠbzFig.11 Moments of inertia Ⅰbz

5 结束语

1）针对太阳帆航天器的姿态机动，采用两种控制手段的组合控制方式，提出了复合控制方法。相比输入成型方法，采用复合控制方法的机动时间更短，还能消除姿态机动过程中的柔性振动，使机动角度的精度更高；

2）当第一阶振动模态对姿态机动影响占主要时，应采用复合控制方法（1），直接根据式（16）和式（17）计算得到Qb1和Pa。而如果前n阶振动模态均对姿态机动有较大影响时，应采用复合控制方法（2），但由于动力学方程是非齐次线性方程组，不能得到解析解，只能通过数值求解；

3）复合控制方法通过已有控制手段的优化组合，实现太阳帆姿态机动的振动抑制，控制算法简单，适合于实际工程应用。

[1]MCLNNES C.Solar sailing：technology，dynamics，and mission applications[M].New York：Springer-Praxis，1999.

[2]WIE B.Solar sail attitude control and dynamics，part 1 [J].Journal of Guidance，Control，and Dynamics，2004，27（4）：526-535.

[3]WIE B.Solar sail attitude control and dynamics，part 2 [J].Journal of Guidance，Control，and Dynamics，2004，27（4）：536-544.

[4]WIE B，MURPHY D.Solar-sail attitude control design for a sail flight validation mission [J].Journal of Spacecraft and Rockets，2007，44（4）：809-821.

[5]SLEIGHT D W，MUHEIM D M.Parametric studies of square solar sails using finite element analysis [C].45thAIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics ＆ Materials Conference，California，USA，April 19-22，2004.

[6]LI QING，WANG TIANSHU，MA XINGRUI.Reduced model of flexible sail-boom interaction for solar sail dynamics[C].60thInternational Astronautical Congress，Daejeon，Republic of Korea，2009.

[7]崔乃刚，刘家夫，荣思远.太阳帆航天器动力学建模与求解 [J].航空学报，2010，31（8）：1565-1571.CUI NAIGANG，LIU JIAFU，RONG SIYUAN.Solar sail spacecraft dynamic modeling and solving[J].Acta Aeronautica and Astronautica Sinica，2010，31（8）：1565-1571.

[8]张洋.太阳帆航天器姿态控制与轨迹优化研究 [D].合肥：中国科学技术大学，2010.ZHANG YANG.Attitude control and trajectory optimization of solar sail[D].Hefei：University of Science and Technology of China，2010.

[9]崔祜涛，骆军红，崔平远，等.基于控制杆的太阳帆姿态控制研究 [J].宇航学报，2008，29（2）：560-566.CUI HUTAO，LUO JUNHONG，CUI PINGYUAN，et al.Attitude control of solar sailspacecraft with control boom [J].Journal of Astronautics，2008，29（2）：560-566.

[10]崔乃刚，刘家夫，荣思远.柔性太阳帆航天器动力学建模与姿态控制 [J].哈尔滨工业大学学报，2011，43（7）：1-5.CUI NAIGANG，LIU JIAFU，RONG SIYUAN.Study on dynamics modeling and attitude control of flexible solar sail spacecraft[J].Journal of Harbin Institute of Technology，2011，43（7）：1-5.

[11]ZHANG JIN，ZHAI KUN，WANG TIANSHU.Control of large angle maneuvers for the flexible solar sail[J].Science China，2011，54（4）：770-776.

[12]TALEGHANI K B，SLEIGHT D W，MUHEIM D M，et al.Assessment of analysis approaches for solar sail structural response [C].39thAIAA／ASME／SAE／ASEE Joint Propulsion Conference and Exhibit，Huntsville，Alabama，July 20-23，2003.

[13]HU QINGLEI，SHI PENG，GAO HUIJUN.Adaptive variable structure and commanding shaped vibration control of flexible spacecraft[J].Journal of Guidance，Control，and Dynamics，2007，30（3）：804-815.