基于数值实验的信息论课程教学方法

田 园，覃振权，惠 煌

（大连理工大学 软件学院，辽宁 大连 116620）

信息论是当代信息科学的课程体系，特别是网络与通信领域课程体系的核心知识基础，这些课程涵盖数字通信、信号处理、因特网与物联网、无线与移动通信技术、网络多媒体及网络安全等众多领域［1－2］。在概念层面，学生在信息论课程中所学习到的熵、互信息量、信道容量、率失真函数等一系列基本概念为全面领会和掌握其他网络与通信课程的重要概念提供了统一的概念框架［3－6］。在方法层面，由于信息论所研究的是有关信息处理和传输的普遍规律，因此学生在信息论课程所学到的这些规律，以及针对这些规律的分析方法，构成理解和掌握其他众多课程的技术性内容的基石。信息论自诞生以来，始终是处于信息科学领域的前沿学科，其新思想和新成果至今仍不断涌现、发展迅猛，对当代信息科学，特别是网络与通信科学领域所起的作用越来越举足轻重［2－3，7－8］。也正是在这里，这一课程的传统教学方法已越来越难以适应信息论学科及其应用的发展需要，亟须探索相应的新手段和方法。

1 基于数值实验的新教学方法

1.1 传统讲授方法面临的瓶颈

信息论课程的性质在传统上属于理论型课程，因此对其核心概念与规律的讲授方法主要侧重于理论分析。目前这种教学方法面临以下瓶颈，亟须解决：

（1）以理论分析为主的教学方法要求学生具备较为全面的数学基础和较强的抽象思维能力，因而在很大程度上限制了在本科阶段建立起较为扎实的信息论知识基础与运用能力。

（2）当前，信息论以前所未有的广度与深度渗透于当代信息技术的各个分支，由此对IT工程师在技术创新与研发中熟练运用信息论的基础知识的能力提出了前所未有的高要求［3，6－7］。然而传统的教学方法难以使大多数学生对信息论基础知识获得准确和深入的认知，从而影响了他们对信息论知识的应用能力。

1.2 新教学法思路

面对以上挑战，我们在教学实践中探索一种基于数值实验的新教学方法教授信息论。通过2年多的不断实践与改进，取得了较为显著的成效。采用这一新方法的思路归纳如下：

（1）从分析本科阶段信息论“难学”的根源出发，发现学习的难点并不完全在于要求较多和较深的数学预备知识，更为本质的难点在于信息论这一学科本身的很多规律属于所谓“概率范畴的精确规律”［8］，例如作为理解信息论诸多规律基础的独立随机变量的大数定律以及渐进典型集合的奇特性质。这类科学规律与经验、直觉迥异，仅从理论分析（虽然并不复杂）本身来解释，初学者仍感到抽象和神秘，也就难以运用。为此，需通过新的教学方法来帮助学生认知和领会这类科学规律的精髓。信息论的其他核心规律，如信道编码的Shannon定理和率失真定理等，也都有类似情形。

（2）当今信息论对众多网络技术领域的应用，不仅强调模型的理论分析，而且日趋强调通过大规模数值计算来解决实际问题［6－7］。传统的以理论分析为主的教学方法已不适应这一学科发展趋势，亟须建立一种更为面向工程应用的教学方法，使学生在未来能够顺利地从“所知”过渡到能够“所用”。

1.3 基于数值实验的信息论课程教学新方法

基于数值实验的信息论课程教学新方法的实质，是以计算机软件为工具，实现对典型信道、信源、网络等实体的建模，在此基础上通过数值计算来展示相应的科学规律。较之传统的以理论分析为主的教学方法，以及主要用于验证目的的仿真实验教学方法［9－15］，这一新方法有以下优点与特色：

（1）使以往较为抽象的概念模型与规律具体化和形象化，便于学生准确理解，尤其强调学生通过开放的实验软件自主观察，并以实验观察为基础提出问题。

（2）由于信息论的众多模型本质上属于概率性模型，因此理论分析仅能限于概率估计和均值分析，初学者很难借此准确领会这些分析结论的具体涵义，而数值实验则可以在真正随机（而非“平均”）的意义上来进行，使学生直接看到真正的随机过程的结果与规律，这对学生领会那些“概率范畴的精确规律”尤有助益。

（3）当前信息论的主要发展趋势之一就是越来越多的理论成果表现为针对求解各类实际应用问题的算法形式［6－7］，基于数值实验的教学方法与信息论的学科这一发展趋势完全一致。

基于数值实验的信息论课程教学方法，不是简单补充传统的理论分析型教学或仅为理论分析提供验证，而是既为理论分析提供验证，同时也作为引导正确的理论分析与结论的启发性方法。在这里，传统的理论分析教学环节恰好成为验证数值实验观察结果的一个步骤（见图1）。我们的教学实践表明，后一种功效对学生更有价值，它也往往极大地激发起学生深入探索的兴趣与热情。这一特点也与数值实验在信息论研究中的角色相一致。

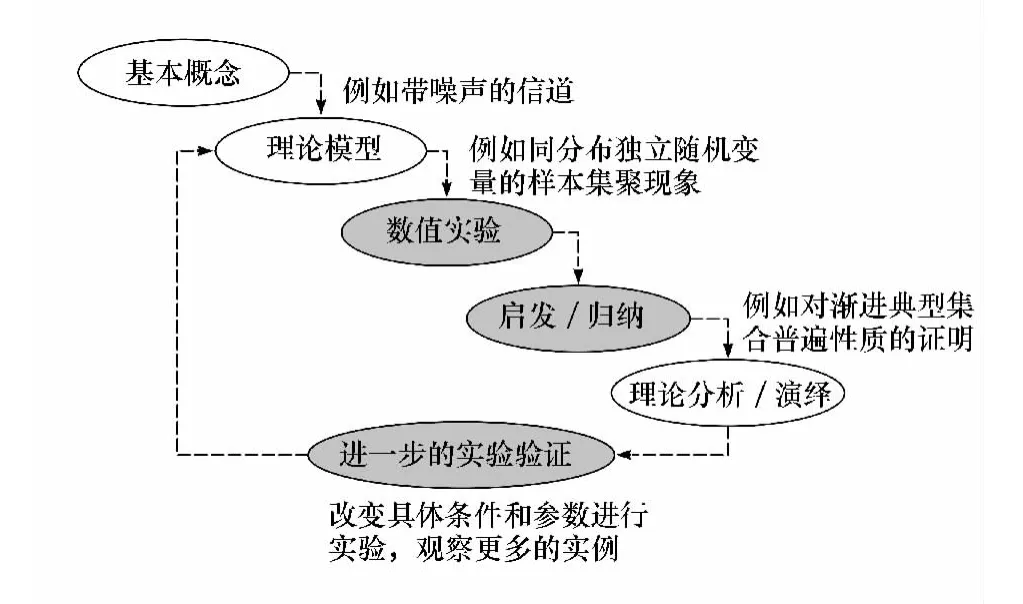
图1 数值实验在信息论课程教学中的角色（阴影部分）

2 基于数值实验的信息论课程教学案例

上一节概述了基于数值实验的信息论课程教学方法的主要思想与特点，这一节具体阐述2个典型的教学案例。

（1）案例之一是作为信息论领域众多科学规律基础的渐进典型集合的性质。这一规律反映了熵这一信息论核心概念的本质特征。概括地讲，渐进典型性质是说，一组独立的同分布随机变量x1，…，xn无论具有怎样特殊的概率分布，总存在这样一种样本子集，随着n的增长，该子集相对于总体样本数量所占比例越来越小，而样本落在该子集中的概率却越来越大，并最终接近1。对这一显著异于直观经验的统计规律采用数值实验方法进行教学，我们为学生展示以下数值实验。

输入参数：

独立随机变量的个数n；参数ε；随机变量X遵循的概率分布P［X］等。这些输入可由学生任意设置。

数值计算步骤：

①根据随机变量的概率分布计算熵H［X］；

②计算出样本集An（ε）＝ ｛（x1，…，xn）：2－n（H［X］＋ε）≤p（x1，…，xn）≤ 2－n（H［X］－ε）｝；

③根据概率分布P［X］生成足够多的联合样本（x1，…，xn），并实际统计落在集合An（ε）中的样本所占比率（%）并以直方图显示；

④增大n，重复步骤1到3，并观察落在集合An（ε）中的样本所占比率的变化趋势；

⑤降低ε，重复步骤1到4并观察落在集合An（ε）中的样本所占比率的变化趋势；

⑥改变X的概率分布，重复步骤1到5并观察落在集合An（ε）中的样本所占比率的变化趋势。

该实验简单易行，同时真实可信，学生经常出于好奇设计出各种概率分布进行反复实验，但最终所观测到的趋势总是惊人地一致，即#An（ε）≤2n（H［X］＋ε）且n足够大时P［An（ε）］＞1－ε。图2是一组数值实验的统计实例。

图2 渐进典型集合数值实验统计输出柱形图

在确信这一反复出现的实验规律的基础上，再进行理论分析和演绎证明，学生不仅容易接受这一证明，而且对这一重要的基础规律的理解不再停留于抽象的表达式层面，而是切实领会到这一统计规律的内涵。

（2）案例之二是二元对称噪声信道上的线性分组编码的译码差错概率与信道容量之间的关系，即Shannon定理。这一普遍规律的理论分析对绝大多数初学者较为复杂和抽象，我们通过数值实验方法进行讲解。

输入参数：

二元对称信道的差错概率p，p的数值由学生任意设定；

2－进制线性分组编码的信息位数k和码字位数n。

数值计算步骤：

①随机生成n行、k列的2－进制满秩编码矩阵G；

②计算G的校验矩阵H和该随机码的最小Hamming重量d；

③计算译码表；

④按照输入的二元信道参数p随机生成信道噪声样本，同时按照均匀分布随机生成码字样本w，对r＝w＋z进行极大似然译码计算；

⑤重复步骤4足够多次并计算译码差错事件所占的比率Pe（n）；

⑥改变k和n，重复步骤1到5并分别统计k／n＜Cp和k／n＞Cp（Cp是参数为p的二元对称信道容量）情形下Pe（n）随n的变化趋势。

随机改变信道参数p和编码方案，重复以上数值实验和观察。在各种情况下，学生可以看到普遍的趋势是在k／n＜Cp时Pe（n）随n增大而下降到0，而在k／n＞Cp时Pe（n）并非随n下降到0。

对以上规律进行理论分析，就是编码差错概率与信道容量关系的Shannon定理（数值实验的统计输出参见图3，其中纵坐标为线性分组编码的译码差错概率，横坐标为信噪比）。

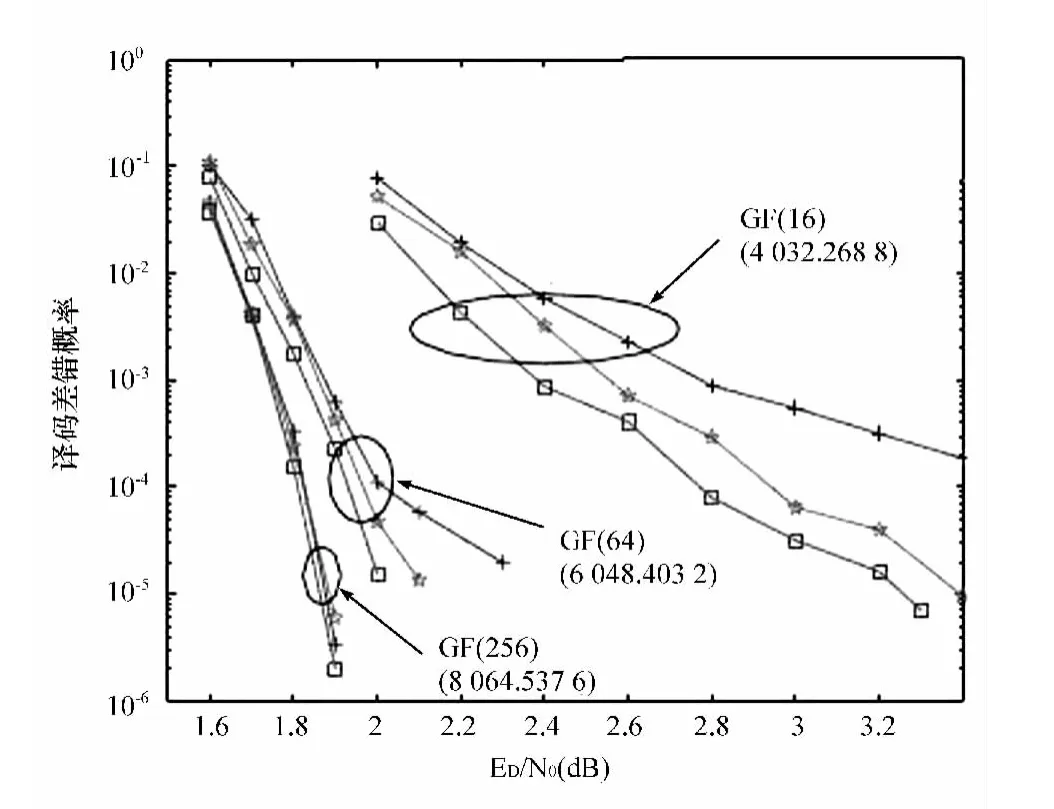
图3 几种线性分组编码方案的译码差错概率随信噪比的变化趋势

3 信息论数值实验软件

实现数值实验教学的软件作为大学生创新项目，由参与信息论课程学习的学生在教师指导下设计开发，基于Java编程实现并以浏览器－服务器架构在网络环境下交互式运行，成为学习信息论课程的一种综合数值实验环境。目前该软件可以实现的主要数值实验类型有：大数定律数值实验；各类渐进典型集合的数值实验；各类噪声信道（离散二元对称信道、高斯噪声连续信道等）的建模及信道容量计算；对典型的线性分组编码（如循环码）及随机分组编码的译码计算和参数计算；对各类信源建模及其率失真函数的计算。该软件目前仍在继续完善，例如扩展到针对网络模型的容量计算和针对衰落信道的建模与数值实验。

4 结束语

我们在分析学生掌握信息论课程知识的关键障碍的基础上，提出了基于数值实验的新教学方法，其实质是以计算机软件为工具，实现对典型信道、信源、网络等实体的建模，并在此基础上通过数值计算来展示信息论独特的科学规律。论文分析了该方法的特点与优势，并以渐进典型集合的性质及Shannon定理的教学为例，详细阐述了具体案例。教学实践充分证实了该方法的优势与潜力，目前在总结以往教学实践成果的基础上，在教学内容及数值实验软件的功能方面继续完善和提高。

（References）

［1］Cover T，Thomas J A.信息论基础［M］.阮吉寿，张华，译.北京：机械工业出版社，2010.

［2］Tse D，Vasvanath W.Foundations on Wireless Communications［M］.New York：Prentice－Hall Inc，2005.

［3］林闯.计算机系统与计算机网络中的动态优化：模型、求解和应用［J］.计算机学报，2012，35（7）：1339－1357.

［4］林舒，Coestello R.差错控制编码理论及应用［M］.北京：机械工业出版社，2009.

［5］仇佩亮，张朝阳，杨胜天.多用户信息论［M］.北京：高等教育出版社，2012.

［6］王育民，李晖，粱传甲.信息论与编码理论［M］.北京：高等教育出版社，2008.

［7］Verdu S.Fifty Years of Shannon Theory［J］.IEEE Trans On Information Theory，1998，44（6）：2057－2078.

［8］卓里奇A.自然科学问题的数值分析［M］.周美珂，李植，译.北京：高等教育出版社，2011.

［9］李仕强，王水平，李翔.基于Web的虚拟实验互动教学平台研究与设计［J］.实验技术与管理，2012，29（11）：90－93.

［10］张鸣，李白萍.Matlab仿真在通信原理课程中的应用［J］.实验技术与管理，2012，29（11）：87－89.

［11］宋金铃，蔡丽.扩频通信系统实验的仿真设计［J］.实验技术与管理，2008，25（9）：86－88.

［12］昌彦君，张莹，曹中林.探地雷达数值模拟实验研究［J］.实验技术与管理，2009，26（4）：69－72.

［13］常山，毛杰健，桑志文，等.高斯光束微圆孔衍射变换的数值仿真实验［J］.实验技术与管理，2011，28（1）：80－83.

［14］刘艳莉，金文，陈志敏，等.网络通信在基于LabVIEW虚拟仪器仿真系统中的应用［J］.实验技术与管理，2011，28（1）：44－76.

［15］李敏，邹涛，杨马英，等.过程控制系统综合性实验设计与教学实践［J］.实验技术与管理，2011，28（6），100－104.