制冷系统用单向阀动力学模型研究

叶奇昉，刘杰，陈江平

（1-上海汽车集团技术中心，上海 210804；2-上海交通大学，上海 200240）

0 引言

单向阀作为最简单的自控元件在不同类型的制冷系统中有广泛的应用。然而单向阀在某些特定工作条件下中经常出现工作不稳定的情况，表现为：阀门不断开闭，阀芯敲击阀座产生很大噪声，整个制冷系统工况不稳定。前人针对直动式阀件动力学特性研究有一定基础，但研究对象大多数针对不可压缩流体[1-5]。研究方法主要以仿真研究为主，在研究过程中对系统进行的简化过多，所建立的模型不能很好地反映出阀芯与流体的相互作用。

本文首先对阀内流动进行 CFD研究，获得不同工作压力、工作流量条件下单向阀阀芯受到的流体作用力；然后基于流固相互耦合作用建立单向阀动力学模型，并对不同工作条件下的单向阀工作状态进行可视化实验研究，通过实验结果验证模型的准确性。

1 单向阀系统动力学模型

典型的制冷系统用的单向阀如图 1，当流体从进口流入时，流体作用力推动阀芯向右移动导致阀门开启，流体流出；当流体流向相反时，流体作用力导致阀芯左移，阀门关闭。

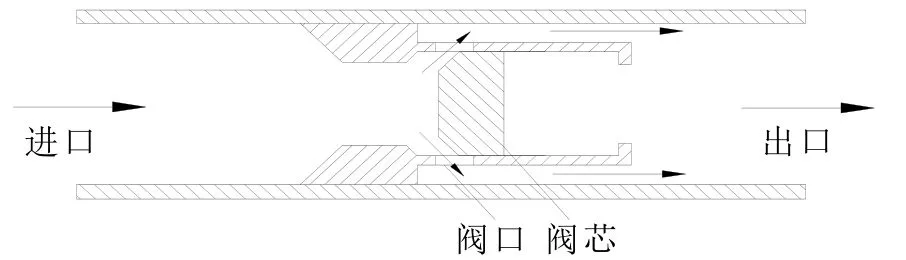
图1 单向阀结构示意图

1.1 阀芯流体作用力的CFD研究

阀内结构相对复杂，因此本文采用 CFD方法针对以氮气为工质的单向阀进行仿真研究。对不同进口压力、出口流量、阀门开度时的阀内流场进行了模拟，以获得不同条件下单向阀阀芯受到的流体作用力。

图2为单向阀模型的面网格图。由于结构相对较复杂，采用四面体与六面体两种网格相结合的方法对阀内网格进行划分。图2所示结构共包含四个部分：进口流道、喉部流道、阀口流道和出口流道。

图2 单向阀网格划分示意图

采用带有壁面函数的标准κ-ε湍流模型，湍流度为5%。采用一阶离散方法来求解流场方程，求解收敛标准为残差10-3。

为了获得阀芯的流体作用力采取的边界条件为：进口压力边界条件，出口流量边界条件。计算的具体工况如表1。

表1 计算工况

阀芯受到的流体作用力与进口压力的关系如图 3。由图可知，随着进口压力的升高，流体作用力呈近似线性增加。阀芯受到的流体作用力与进口流量的关系如图 4。由图可知，随着进口流量的升高，流体作用力呈近似二次方关系增加。

流体作用力与阀门开度的关系如图 5。由图可知：当阀门开度小于0.4 mm时，随着开度的增加流体作用力急剧降低；当阀门开度大于0.4 mm时，随着开度的增加流体作用力逐渐降低，但降低的趋势变缓。

图3 流体作用力与进口压力的关系

图4 流体作用力与进口流量的关系

图5 流体作用力与阀门开度的关系

1.2 单向阀系统动力学模型

单向阀动力学研究对象包括单向阀本身及其上下游管路中的气体。图6为单向阀系统示意图，包括气源、上下游调节阀、上下游管路、单向阀。上游气源中压力为pu，稳定状态下单向阀上、下游调节阀中流量分别为Qs与Qd。

图6 单向阀系统示意图

Qs与 Qd为流经上下游调节阀的流体流量，分别可以表示为：

式中：

Cd——调节阀的流量系数；

Au, Ad——上下游调节阀的流通面积，对于确定工况为常数；

pu——气源中流体压力；

ps——上游管路中流体压力；

pd——下游管路中流体压力；

ρu——上游气源中流体密度；

ρa——上游调节阀出口的流体密度。流经单向阀的流体流量为：

式中：

Cc——单向阀的流量系数，由CFD计算得出；

Ac——单向阀的阀口流通面积；

pin, pout——单向阀进出口压力。

当单向阀上下游管路长度大于0.3 m时，必须考虑管路中压力波传递，管内速度压力波动可由流体的连续方程与动量方程描述：

式中：

u——流体速度；

a——流体中声波速度。

假设阀芯振动过程为单自由度运动，阀芯振动取决于：阀芯质量、流体作用力、阻尼力；其振动方程可表示为：

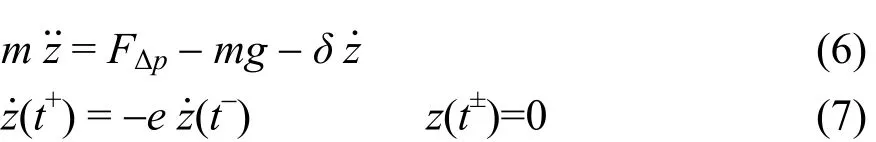
式中：

m——阀芯质量；

δ——阻尼系数；

e——恢复系数；

FΔp——不同条件下的流体作用力，FΔp由CFD仿真获得。

综上所述，单向阀系统的动态模型为式(1)～式(7)，对系统动态特性进行模拟时，采用四阶龙格-库塔法模拟阀芯振动，采用特征线法模拟阀上下游管路中的压力波动。

2 实验台简介

为了研究单向阀在不同工作条件下的动力学特性，对阀芯振动进行了可视化研究。如图7所示，实验系统包括氮气气瓶、管路、调节阀、压力传感器、压力表、可视化单向阀、压差传感器、高速照相机以及体积流量计。

实验针对不同进口压力、出口流量，实验工况如表 2。实验过程中，针对不同进口压力准静态地增加出口流量直到阀芯停止振动为止。

图7 实验台原理图

表2 实验工况

3 动力学模型验证

当准静态地增加进口流量，单向阀的工作状态如图 8。由图可知，当进口流量较小，进口压力较低时，单向阀的工作状态在A区域，此时阀芯在阀内产生稳定的振动，单向阀工作不稳定；随着进口流量与进口压力的增加，振动将在某一临界流量停止，工作状态进入B区域，此时阀芯静止于阀内，单向阀工作稳定。图8比较了临界流量的仿真结果与实验结果，并基于实验结果采用最小二乘法获得阀芯运动时的阻尼系数。由图可知：动力学模型能够较为准确的预测单向阀稳定工作区域，判断单向阀的工作状态。

图8 进口流量准静态增加时单向阀工作状态

当单向阀工作条件处于图8中A区时，阀芯将出现稳定的振动，振动频率实验结果与仿真结果如图 9。由图可知：对于不同的工作状态，阀芯振动频率的仿真结果与实验结果较为接近，动力学模型能够准确的预测进口压力、进口流量对阀芯振动频率的影响。

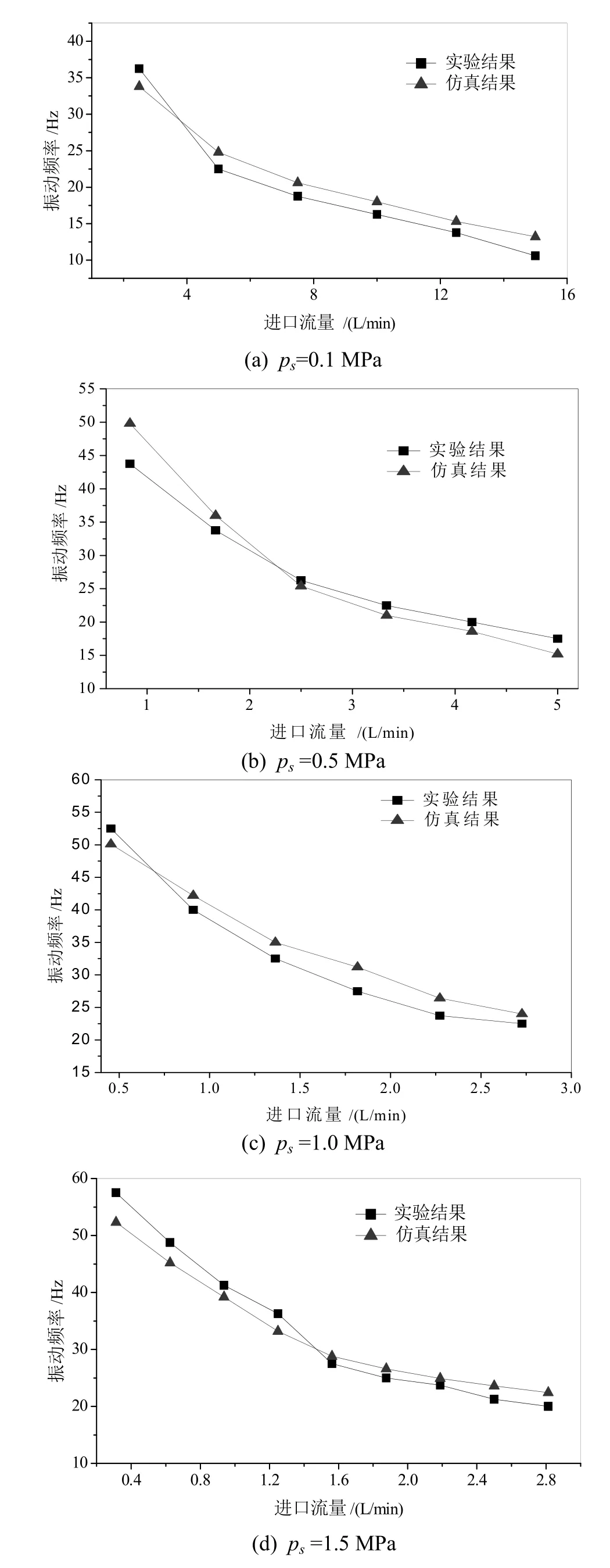
图9 不同工作条件下单向阀阀芯振动频率

4 结论

本文基于系统内流体与阀芯的相互耦合作用，建立了制冷系统用单向阀系统的动力学模型。不同工作条件下阀芯振动的可视化实验研究结果表明：该模型能够比较精确地预测单向阀的不稳定工作区域，确定单向阀在不同条件下的工作状态。当阀芯不稳定工作时，对于不同的工作条件，阀芯振动频率的仿真结果与实验结果较为接近，动力学模型能够准确的预测进口压力、进口流量对阀芯振动频率的影响。实验结果验证了动力学模型的准确性，该模型可以作为单向阀动力学分析的工具。

[1] HAYASHI S, IZUKA I Y, HAYASE T. Numerical treatment of discontinuity due to collision[J]. Hydraulics and Pneumatics, 1994, 25: 439-445.

[2] HAYASHI S, OHI K. Global stability of a poppet valve circuit[J]. Journal of Fluid Control, 1993, 21: 48-63.

[3] HAYASHI S, HAYASE T, KURAHASHI T. Mechanism of hard self-excited vibration in poppet valve (the case of large valve lift)[C]// In Proceedings of 4th International Symposium on Fluid Control, Measurement and Flow Visualization, Toulouse, France, 1994, 2: 641-646.

[4] HAYASHI S, HYASE T, KURAHASHI T. Chaos in a hydraulic control valve[J]. Journal of Fluids and Structures, 1997, 11: 693-716.

[5] MISRA A. Self-excited vibration of a control valve due to fluid-structure interaction[J]. Journal of Fluids and Structures 2002, 16(5): 649-665.

[6] HAYASHI S. Instability of poppet valve circuit[J]. JSME International Journal, 1995, 38: 357-366.