海杂波对舰载雷达探测效能影响评估＊

鞠增彪 王继光 孙鹤泉 黄鹏飞 李金堡

（海军大连舰艇学院军事海洋系 大连 116018）

1 引言

在现代高技术条件下海上局部战争中，水面舰艇编队要圆满完成上级赋予的作战任务，不但要拥有先进的武器装备，更要拥有先进的信息获取设备，也就是说未来海上高技术条件下局部战争的胜负在很大程度上将取决于信息的获取能力［1］。

舰载雷达作为海军的电子眼，是海上信息战的重要信息来源，是舰载武器系统的重要组成部分，担负着警戒搜索、跟踪制导、舰载机引导以及气象探测等重要任务。雷达的性能优劣直接影响舰艇的作战能力，影响整个作战进程，甚至决定战争胜负［2］。

由于海上作战环境复杂，雷达的探测距离不仅仅受到雷达技术的限制，必然还会受到海洋环境的影响，有时甚至极大地制约雷达的探测范围，使水面舰艇成为“瞎子”，无法完成任务。

影响雷达探测的主要海洋环境要素有风场、温度场、湿度场、海浪等。本文从海面风场对雷达探测距离的影响入手，将风速、风向两个风场要素对雷达探测距离的影响程度进行建模评估，从定性的分析转变为定量的分析，得到一个量化的效能指标，为战场环境保障决策提供一个科学、可信的数据支持，具有重要的军事意义和应用价值。

2 建模过程

2.1 选择影响因子和评价标准

指数法是构建效能指标的一种重要途径，其实质是用某个统一尺度（效能指标）来度量待评估武器装备相对于某参考武器装备的作战效能，从而得到待评估武器装备的效能指数。将各类效能指数按照一定的规则融合集成即可得到待评估武器装备的总效能指数［3］。

本文以舰载雷达为待评估的武器装备，重点研究在海面风场的影响下舰载雷达探测距离的效能评估，并建立了数学模型进行仿真实验。在风场的作用下，海面形成风浪，使得海面粗糙度增加，雷达接收到电磁波照射海面后产生的回波，即海杂波，也会随之增大。因此海面风场对雷达探测距离的影响主要通过海杂波的形式表现出来。风场最基本的两个要素是风速和风向，这两个要素都可以方便快速地在海上直接测量得到，而且它们可以直接影响到雷达探测距离的大小。所以本文选择风速影响因子和风向影响因子作为基本影响因子，选择雷达探测距离的大小作为评价标准。

给定风速条件下雷达最大探测距离和标准条件下雷达最大探测距离的比值称为风速影响指数fws。给定风向条件下雷达最大探测距离和标准条件下雷达最大探测距离的比值称为风向影响指数fwd。将这两个基本影响指数进行融合集成，即可得到给定风场条件下雷达探测的总效能指数fw。

由于风速影响和风向影响相互独立，所以可以用乘法关系来融合集成两个基本影响指数，即fw＝fws·fwd。

2.2 雷达探测距离和海杂波关系

舰载雷达在工作中接收到的信号由反射波和接收机本机噪声组成，其中反射波分为目标回波和海杂波两种。目标回波强度和噪声强度的比值称为信噪比，当不考虑接收机本机噪声时，噪声主要就是海杂波，这种情况下，增大雷达发射功率并不能增大探测距离。这是因为当发射功率增大时，目标回波和海杂波会同步增大，这已为实际情况所证实［4］。

雷达探测目标作用距离主要受到海杂波的限制，当信噪比高于某极限值时，雷达即可识别目标，达到探测目标的目的，反之，当信噪比低于该极限值时，雷达无法探测到该目标。对于固定目标，如对方水面舰艇、潜艇等，回波的强度一般是固定的，因此通过对海杂波的研究可以使我们得到雷达探测距离随风场的变化规律［5］。

雷达最大探测距离公式如下［1］：

其中，R为雷达探测距离；C为雷达参数，对于固定型号雷达，为常数；σs为目标的雷达反射面积；（S／N）req达到一定检测概率下所需的信噪比。

当信噪比增加α倍时，探测距离就会相应减小即

其中，R0为标准状态下雷达最大探测距离。

可以看到，当海杂波强度越大时，信噪比也越大，雷达探测距离就会下降。反之，海杂波强度越小，信噪比也越小，雷达探测距离越大。

2.3 海杂波反射系数的变化情况

海杂波强度可用海杂波反射系数来表示，海杂波反射系数的大小取决于入射余角、电磁波频率、极化方式和海况。彭世蕤等给出了海杂波等效反射系数与海况、入射余角和频率之间关系的近似模型［6］：

式中Ss为海况，用来描述海面风场；θg为入射余角；λ为雷达工作波长；β＝［2.44（Ss＋1）1.08］／5.73；θc＝为海面粗糙度；

k取值范围1～4，建议取值1.9，雷达工作波长取3cm得到不同海况下海杂波反射率随入射角度变化曲线如图1。

可以看到海杂波反射率变化情况随着入射余角的变化可以明显分为三个区域，干涉区、平稳区、准镜面区。在入射余角很小时（0°～5°），海杂波反射率随角度增加而增加，且速度较快，这一区域称为干涉区。随着入射余角增加（5°～85°），海杂波反射率增加较慢，这一区域称为平稳区。在靠近90°附近时，海杂波反射率急剧增加，这一区域称为准镜面区。

图1 海杂波反射强度随入射余角变化曲线

2.4 入射余角和距离的关系

入射余角和雷达与目标之间距离的关系式［7］：

其中，ha为雷达高度；R为雷达和目标之间距离；ae为地球等效半径，一般为8493km。

当雷达高度为15m 时，可得到入射余角和雷达与目标之间距离的关系曲线。

一般雷达探测范围在几公里到几十公里的量级上，从图中可以看到在这个范围内，入射余角在0°～5°之间，处于干涉区。

2.5 海况-风速-波高之间关系

当前用的海面状态标度有两种——蒲福（Beaufort）标度和多格拉斯（Douglas）标度。蒲福标度偏重于风向而不是海浪方向，所以用多氏标度描述海杂波更合适［8］。

表1 海况-风速-浪高-关系表

多氏标度中浪高采用的是三分之一有效波高h1／3，取值为所有波浪中三分之一最大振幅波动波高的平均值。而由Nead 修正的GIT 模型中计算时使用的时平均波高havg，取值为所有波动波高的平均值。由经验公式可知两者换算关系为

图3 风速-波高拟合曲线

通过二次曲线拟合，得到风速和波高的关系式：

2.6 海杂波和雷达极化之间的关系

海杂波强度和雷达极化的关系在不同海况、频段、入射余角情况下会有所不同。一般来说，在平静海面，垂直极化下海杂波强度大于水平极化；风浪较大时，两种极化下海杂波强度值相接近；在低入射余角时，水平极化下海杂波强度会大于垂直极化［9］。

由于舰载雷达探测范围内绝大部分区域属于低入射余角区域，所以本文选取垂直极化方式。

2.7 修正的GIT 模型

对于小入射余角的情况，可以参考由Nead修正的GIT模型［10］，修正后的模型可以拓展应用于蒸发波导条件下视距外小入射余角的情形。

对于水平极化

对于垂直极化

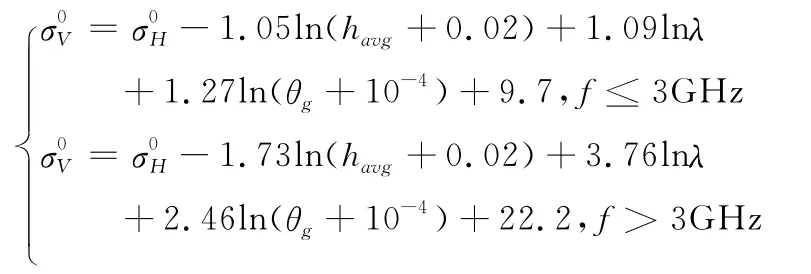
式中为水平极化条件下海杂波反射率为垂直极化条件下海杂波反射率；λ为雷达工作波长；θg为入射余角；Aw为风速项；Au＝exp［0.2cosφ（1-2.8θg）（λ＋0.02）-0.4］为风向项；为干涉项；ωs为风速；φ为雷达天线轴线和逆风向之间的夹角（0°～180°）；为粗糙度因子；havg为平均波高。

3 仿真实验

3.1 风向因子对雷达探测效能影响

当风速为15m／s时，令风向和雷达之间夹角分别为0°，30°，60°，90°，120°，150°，180°。雷达高度15m，雷达工作波长3cm，得到海杂波反射率随距离变化关系如图4所示。

图4 不同夹角下海杂波强度随距离变化曲线

从图中可以看到，随着风向和雷达之间夹角φ由0°（逆风）增加到180°（顺风），海杂波反射率逐渐减小，信噪比逐渐减小，雷达最大探测距离逐渐增大。令风向和雷达夹角180°（顺风）时雷达效能为1，得到不同风向下雷达探测效能情况如表2所示。

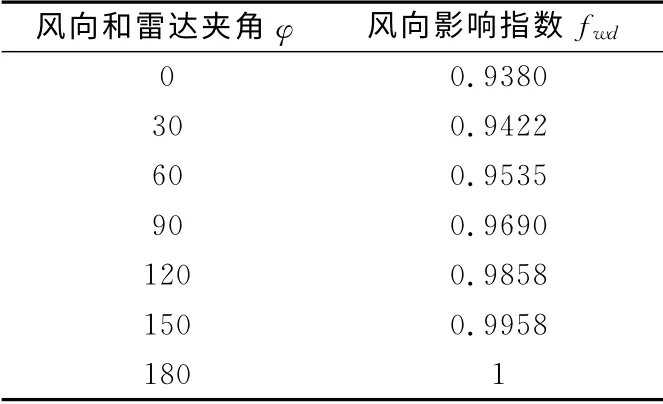
表2 不同风向下雷达探测效能（风向和雷达夹角180°）

3.2 风速因子对雷达探测效能影响

由风向因子对雷达探测效能影响分析可知，当顺风时，雷达探测效果最佳，所以令风向和雷达夹角φ为180°，风速分别设置为3m／s，6m／s，9m／s，12m／s，15m／s，18m／s，21m／s。雷达高度15m，雷达工作波长3cm。得到海杂波反射率随距离变化关系如图5所示。

图5 不同风速下海杂波强度随距离变化曲线

从图中可以看到，随风速增加，海杂波反射率逐渐增加，信噪比逐渐增大，雷达探测距离逐渐减小。令风速为3m／s时雷达探测效能为1，得到不同风向条件下雷达探测效能情况如表3所示。

表3 不同风向条件下雷达探测效能（风速为3m／s）

3.3 给定风场环境下雷达探测效能指数

给定风场环境：风向和雷达夹角120°风速15m／s。

由3.1和3.2中讨论可知，该风场环境下，风向影响指数fwd＝0.9858，风速影响指数fws＝0.5037。由影响指数的融合集成关系可以得到改风场环境下，雷达总的探测效能指数为fw＝fwd·fws＝0.4965。

可以看到在风向和雷达夹角120°风速15m／s的条件下，雷达无法完全发挥出正常效能，其最大探测距离只有标准条件下的50%左右。

4 结语

1）当雷达轴线处于处于顺风状态时，雷达可获得最大探测距离。随着两者夹角增大，雷达探测距离逐渐减小，当雷达轴线处于逆风状态是，其最大探测距离只有顺风时的93%左右。在进行探测时，应尽量使雷达轴线处于顺风状态，以获得最大探测距离，最大限度的发挥雷达探测效能。

2）随着风速的增大，雷达的作用距离逐渐减小，当风速达到15m／s时，雷达最大探测距离已经下降到标准条件下的50%。此时海面状态已经十分恶劣，不适于执行海上任务，应尽量避免在这种环境下出海作业。

3）在对海杂波的影响中，风速的影响程度远远大于风向的影响程度，前者对于雷达探测距离的削弱可达到后者的十倍以上。

本文利用GIT 模型对风场影响下的雷达探测效能进行了评估，得出了风速风向对雷达探测距离的定量影响结果，可以为海上执行任务时雷达的作业条件提供科学参考。但是由于海洋环境要素对雷达探测效能的影响机制十分复杂，模型中很多经验公式需要在实践中进一步检验和完善。

［1］郭万海，赵晓哲.舰载雷达效能评估［M］.北京：国防工业出版社，2003：2-3.

［2］中船重工编写组.海军武器装备与海战场环境概论［M］.北京：海洋出版社，2007：488-490.

［3］郭齐胜，郅志刚，杨瑞平.装备效能评估概论［M］.北京：国防工业出版社，2005：20-21.

［4］焦培南，张忠治.雷达环境与电波传播特性［M］.北京：电子工业出版社，2007：143-144.

［5］贲德，韦传安，林幼权.机载雷达技术［M］.北京：电子工业出版社，2007：39-44.

［6］彭世蕤，汤子跃.地（海）杂波反射率模型研究［J］.空军雷达学院学报，2000，14（4）：1-4.

［7］陈力，晋海军，魏灵.末制导雷达目标检测概率的仿真计算［J］.战术导弹技术，2010，9（5）：96-99.

［8］周怀军，丁士援.噪声干扰条件下雷达检测概率分析［J］.舰船电子对抗，2007，30（6）：6-8.

［9］王红军，王平军，赵宏.噪声干扰对雷达检测概率的影响［J］.现代雷达，2003，25（3）：4-6.

［10］庞云峰，张韧，黄志松.大气-海洋环境对舰载雷达探测效能的影响评估［J］.控制指挥与仿真，2009，31（2）：65-70.