含有内热源的管道换热过程数值模拟与分析

高亚南 张风琴 郑枫 林清丽

山东职业学院土木工程系

0 引言

近几年来，有内部热源的导热与对流换热的耦合传热问题是工程技术领域中常见的一种复杂换热问题，例如太阳能吸热器、微电子设备的冷却，室内火灾分析等等。由于涉及到流体流动与能量传递的耦合，加之具有较高的理论和实用研究价值，许多学者曾对此进行了相当多的实验和数值分析[1～3]。但是，这些研究绝大多数都是仅针对封闭空间内流体冷却介质的流场和温度场的研究。对于开口管道内包括固体热源的耦合传热的数值分析研究甚少。为此，本文拟采用整场求解法对某方形管道内流体冲刷方形固体（内部为均匀内热源）的耦合传热过程进行数值模拟，并研究其流动特性和换热性能，为工程应用提供参考。

1 研究对象及物理模型

本文所研究的物理模型如图1所示，假设：在一个长度为H4的方形管道中装有一个内部为均匀内热源的方形固体，其边长为H2。该固体放置在管道中的位置为H4/H3=2，H1/H3=2，方形管道内流体冲刷方形固体，来流温度为T0，入口流场是均匀的，速度为u0。为了简化计算，也便于在直角坐标系下进行网格的划分，本文近似地把该研究对象看作是二维的、带有内热源的稳态导热与对流换热的耦合传热过程。

图1 方形管道内流体冲刷方形固体的物理模型

2 数学模型的建立

大多数有实际意义的耦合问题都无法获得解析解，而要采用数值解法。在对复杂的耦合换热问题进行数值求解过程中，常采用整场求解法[4]。即把不同区域中（如：固体和流体）的过程组合起来，作为一个统一的换热过程进行求解。为此，需要找到适用于不同区域的通用控制方程。不同的区域采用通用控制方程，区别仅在广义扩散系数及广义源项的不同。这样，不同物质区域的耦合界面处于求解区域的内部。采用控制容积积分法来导出离散方程时，界面上的连续性条件原则上都能满足，这样就省去了区域之间的反复迭代过程，使计算时间显著缩短。因而整场求解的方法是计算耦合问题的一种主导方法，尤其是在预测电子器件的散热特性时几乎是唯一采用的方法。

2.1 耦合传热问题的控制方程

建立整个计算区域内的传热与流动问题的统一控制方程：

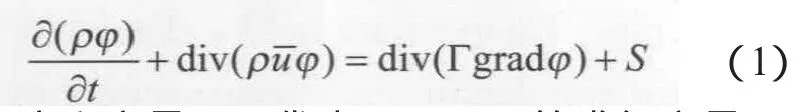
式中：φ为广义变量，可代表u，v，w，T等求解变量；Γ为相应于φ的广义扩散系数；S为与φ对应的广义源项。对于动量方程，把压力梯度放到源项中。u为微元体速度矢量；ρ为密度；t为时间。

式（1）中，左端第一项为非稳态项，第二项为对流项；方程右端第一项为扩散项，第二项为源项。由于只分析温度达到稳定以后的情况，所以简化为稳态问题，略去非稳态项，上述控制方程可化为：

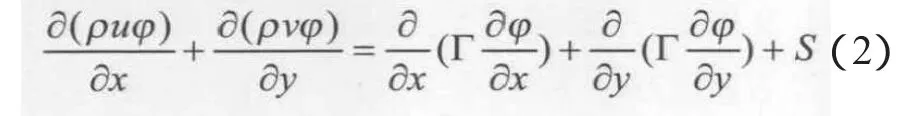
2.2 模型的处理

本文研究的是流固耦合传热问题，同时求解连续性方程、动量方程和能量方程。为了简化问题，先作如下假设：

①空气为不可压缩气体，物性参数为常数；

②流动为层流对流换热；

③不计流体中的粘性耗散；

④流体中的轴向导热略而不计。

2.3 边界条件

根据物理模型，设方形管道的长度为H1+H1=14mm，H4=4mm，H3=2mm，方形管道内的流体为空气，，Pr=0.7，入口空气流速为0.35m/s，温度为10℃，出口为自然出流。方形固体内部均匀内热源q为2000W/m3。考虑到本文主要研究的是管道内部的方形固体与流体间的耦合传热问题，所以计算时假设管道壁面为绝热条件。

3 求解方法

采用整场求解法，对方形管道内流体冲刷方形固体的耦合传热过程，建立统一的数学模型，并在交错网格上对控制方程组进行离散；本文在进行稳态耦合传热数值模拟时采用的是SIMPLE算法；并利用GAMBIT软件对物理模型进行网格划分。采用非均匀网格对计算区域进行划分时，在温度变化较大的区域网格划分的较密，在温度变化较小的区域网格划分的较为稀疏。在对流固耦合问题进行数值求解时应注意如下问题：

1）耦合问题中存在固体与流体区，其内的温度场需要耦合求解，这时固体与流体的分界面上的当量扩散系数应该采用调和平均的方法；

2）在采用整场求解方法时，固体与流体区域中的导热系数采用各自的实际值，但固体区中的比热容则应采用流体区的比热容之值，这样才能保证耦合界面上物理上的热流密度连续；

3）在求解速度方程时，流体区域内网格点的粘度取流体的粘度，而在固体区域内网格点上的粘度则取某个很大的数μ→+∞，同时在与固体相连接的计算边界上设置为无滑移条件。

因此在使用CFD软件数值求解的过程中，必须在物性参数设置、求解方法的选取以及时间步长的确定上特别注意，以保证计算过程中的物理量连续。经过反复试算及改进，得出对于此类流固耦合传热过程的数值模拟。

4 结果分析

本文使用CFD商业软件Fluent进行数值模拟与计算。

4.1 温度场的数值模拟与分析

图2为层流方形管道内流体冲刷方形固体的温度场分布图，其中纵坐标为温度。从上图可知：在管道的入口处，空气温度分布均匀；当流体绕流固体时，固体周围接近固体壁面处的流体温度上升；在固体后表面上下两个拐角区域的温度高于同一截面上的温度，这主要是由于在该区域出现空气漩涡扰动使传热增强；当流体流过固体后，管道内流体的温度受热源的影响较大，可以明显地看出温度分层，温度沿中心轴线向两边递减；随着管长的增加，热源的影响逐渐减小，在出口处温度基本均匀稳定。

图2 方形管道内流体冲刷方形固体的温度场分布图

4.2 速度场的数值模拟与分析

图3，图4分别为方形管道内流体冲刷方形固体的速度场分布图和速度矢量图，其中纵坐标为速度。从图中可以看出：整个流场可以划分为主流区和边界层区（即靠近管壁面处），主流区的速度比较稳定且高于边界层区，靠近管壁面处的流速比较低；在固体的迎风面，由于固体壁面与流体流动方向垂直，所以固体迎风面区域的风速减小；流体接触固体后，从上下两侧绕过，并形成边界层；随后发生边界层脱离固体壁面的现象，并在紧靠固体壁面处产生回流，形成两个对称漩涡，造成固体后表面区域速度减小，经过一段距离后主流区的风速增大并且稍高于入口风速值；由于流体从两侧绕过，所以上下区域的流体速度较大。

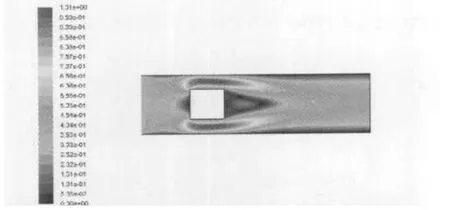
图3 方形管道内流体冲刷方形固体的速度场分布图

图4 方形管道内流体冲刷方形固体的速度矢量图

4.3 Nu数的计算

Nu数表征壁面法向无量纲过余温度梯度的大小，由此梯度反映对流换热的强弱，图5为流体和方形固体壁面之间的对流换热Nu数的变化曲线。从图中可以看出，在方形固体壁面的前端部分，Nu数是非常大的，这是因为此时的边界层最薄，对流换热具有最大值；随着x的增大（即沿着固体水平方向），Nu数急剧降低，这是由于层流边界层厚度的增加，导致局部表面传热系数下降；当x=4.5mm时，在脱体点附近出现Nu数的最低值，随后因脱体区域涡旋的混乱运动，Nu数逐渐回升。图6为流体和方形固体壁面之间的热流量曲线。从图中可以看出，对流换热量与Nu数的变化规律相类似，随着x的增大，热流量急剧减小；当x=4.5mm时，由于受流体涡旋混乱运动的影响换热被加强，热流量开始逐渐增加。

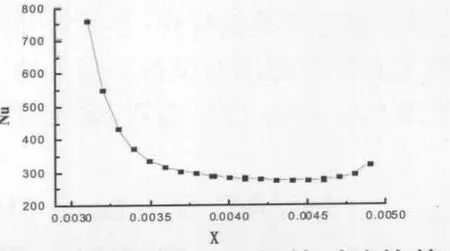
图5 流体和方形固体壁面之间的对流换热Nu数

图6 流体和方形固体壁面之间的换热量

5 结论

本文对方形管道内流体冲刷具有均匀内热源的方形固体的导热及对流耦合传热问题进行了数值模拟，并得出了流体和方形固体壁面之间的对流换热Nu数及换热量的大小。通过结果分析，可以得出如下结论：

1）当流体流过含有内热源的方形固体时，其后的温度场受内热源的影响较大，温度沿管芯向管道壁面递减，热源的影响力沿管长逐渐减小，在出口处温度处于均匀稳定。

2）当流体绕流方形固体时，主流区的速度增大，靠近固体壁面的流体由于粘滞力的影响速度比较低。当流体流过方形固体时，边界层中出现逆向流动，在固体的后表面形成上下两个对称的涡旋。

3）流体和方形固体壁面之间的对流换热Nu数和换热量随着x的增大，急剧降低，这是由于边界层厚度增加的原因，随后因脱体区涡旋的混乱运动，Nu数趋回升。

[1] 姜培学,柯道友,任泽霈.有内部热源的非稳态导热与自然对流换热及辐射换热耦合问题研究[J].计算物理,1999,16(3):302-308

[2] 李明海,陈均,史光梅,等.含内热源球壳的复合传热特性及其表面温度均匀性研究[J].航空精密制造技术,2006,42(2):49-52

[3] 赵琳,胡江峰,刘振侠.流固耦合计算的应用研究[J].沈阳航空工业学院学报,2006,23(4):33-35

[4] 陶文铨.计算传热学(第二版)[M].西安:西安交通大学出版社,2001

[5] 韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2008

[6] 章熙明.传热学[M].北京:中国建筑工业出版社,2001