电动汽车用外转子开关磁阻电机设计与控制系统仿真

韩 帅，王 艳，殷天明

(1.北京交通大学电气工程学院，北京 100044;2.北京联鑫动力科技有限公司，北京 100096)

0 引言

开关磁阻电机(Switched Reluctance Motor，SRM)因为其结构简单、成本低、较高的调速范围、控制灵活且效率高等优点[1]，且有一定的再生制动能力，在电动汽车领域具有更广阔的应用前景。外转子开关磁阻电动轮系统作为轮毂电机系统的一种，可以直接驱动汽车的运行，省去齿轮箱、传动轴等机械结构，提高了电动汽车的效率及可靠性。直接控制电机的运行状况即可控制汽车的运行状况，使得电动汽车的操纵简单。

电动汽车用SRM要求有较小的转矩脉动及一定的再生制动能力，以增加汽车的续航里程。电压及电流斩波控制及角度控制[2]是SRM最常用的控制策略。本文采用有限元软件Ansoft对30 kW的12/8极SRM进行了不同角度、不同电流下稳态磁场的仿真分析，得到的磁链、转矩数据作为MATLAB仿真下的电机数据。其次利用MATLAB/Simulink建立SRM非线性控制模型，在电流斩波，电压斩波及角度控制的基础上，引入模糊电流补偿控制器，对SRM电动状态及再生制动状态进行了仿真。

1 SRM非线性模型

1.1 SRM的数学模型表达式

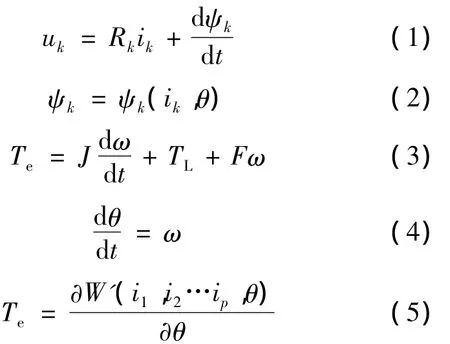
式中:uk——第 k(k=1，2…p)相绕组电压;

Rk——第k相绕组电阻;

ik——第k相绕组电流;

ψk——第k相绕组磁链;

重型血友病患者首次关节出血一般发生在2岁左右，关节出血的发生率随着年龄增长而逐年提高。反复的关节出血易集中在1～2个关节，血友病常累及膝、踝、肘及腕关节，以膝关节最常见，约占49.3%，且关节出血多见于血友病A[11]。

Te——电磁转矩;

J——转动惯量;

F——阻尼系数;

TL——负载转矩;

W'——绕组的磁共能[3]，

为了得到式(2)的磁链与式(5)的转矩的数值关系，本文采用有限元软件Ansoft对SRM进行二维稳态磁场分析，可以较为精确地得到磁链和转矩随角度和电流变化的数据。

1.2 Ansoft电机模型

本文采用的12/8极外转子SRM，参数如表1所示。

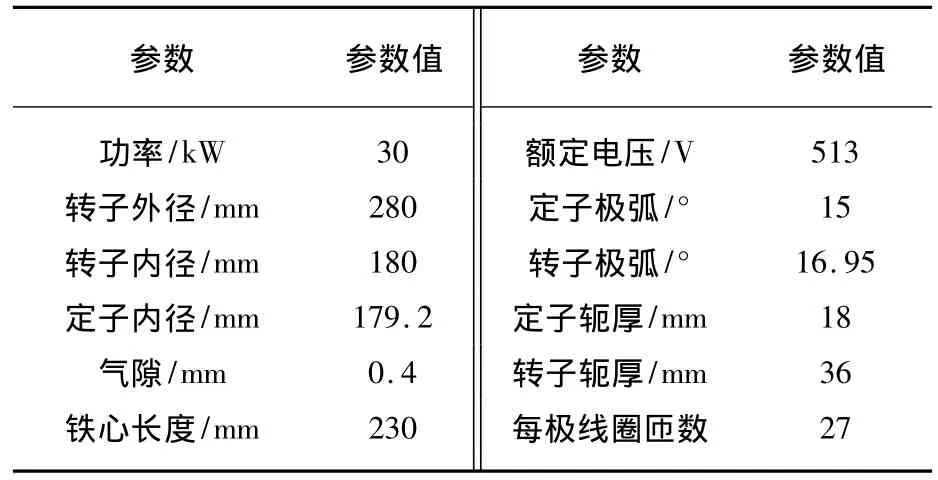
表1 SRM参数

基于Ansoft建立的电机模型[4]如图1所示。

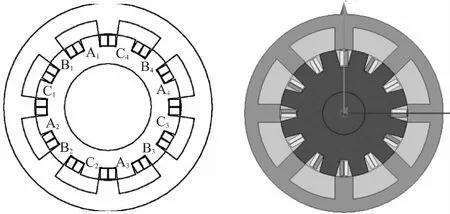
图1 Ansoft电机模型

1.3 Ansoft二维稳态磁场求解

在一个转子位置角周期(0～45°)，电流变化为0，10，20…120 A下的磁链曲线图和转矩曲线图[5]分别如图 2、图 3 所示。

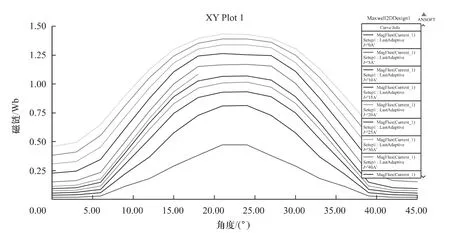
图2 0～120 A磁链角度曲线图

图3 0～120 A转矩角度曲线图

2 SRM系统仿真模型

2.1 单相SRM仿真模型

单相SRM仿真模型主要由电流斩波，功率变换，电流、转矩查表，模糊电流补偿控制器构成。

(1)电流，转矩查表模块。

利用前文30 kW SRM得到的稳态磁场数据，采用数值分析三次多项式插值法，利用MATLAB工具箱将图2反演为i=f(ψ，θ)的数据，结果如图4所示。采用MATLAB二维查表模块。当输入给定的磁链值和角度时，电流模块利用二次插值的算法计算得到最接近的电流值，由得到的电流值与角度值输入转矩查表模块，得到最接近的转矩值。

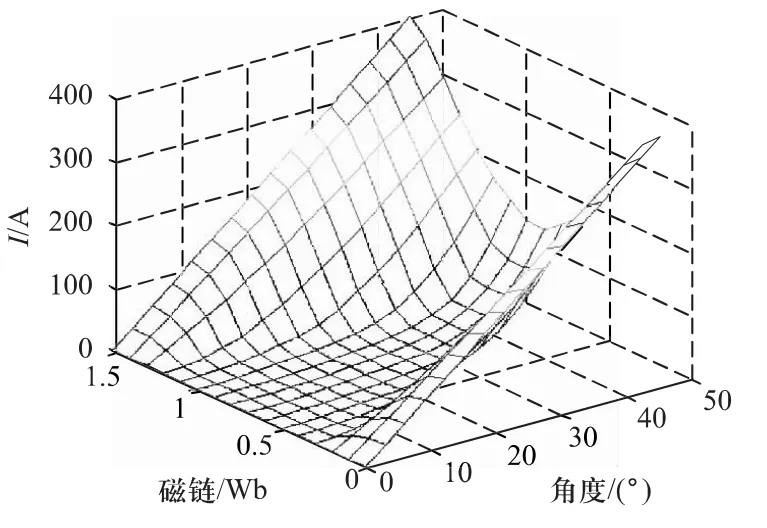
图4 电流反演图

(2)电流斩波模块。

在一个转子周期内，当电流大于斩波上限值ih时，关断开关管，当电流小于斩波下限值il时，开通开关管。管子导通时施加正的电源电压，管子关断时施加负的电源电压，使电流迅速下降为零。

(3)功率变换模块。

电动状态下:当角速度0＜w＜100时，开通角度 θon=2.5°，关断角度 θoff=17.5°，导通电压为513 V。当 w≥100 时，θon=42°，θoff=16°。

制动状态下:当角速度0＜w＜100时，开通角度 θon=22°，关断角度 θoff=31°。w≥100 时，θon=18°，θoff=31°。当 θ＞ θoff时，绕组施加负的电压513 V，使电流在下一周期开始前下降为零。

(4)模糊电流补偿模块。

为减小转矩脉动，引入模糊电流补偿模块[7]。根据图3转矩特性曲线，在角度偏小和偏大区域，转矩的回落幅度最大，在此区域补偿较大的电流，以减小转矩的回落。在其他区域补偿较小的电流或者不进行补偿。

模糊控制以电流值和角度值作为输入，补偿电流为输出[8]。电流值和角度值各分为七个语言值。分别为 NB、NM、NS、Z、PS、PM 和 PB。其补偿电流隶属函数如图5所示，电流补偿的模糊规则表见图6。

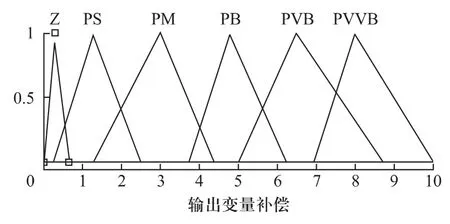
图5 补偿电流隶属函数

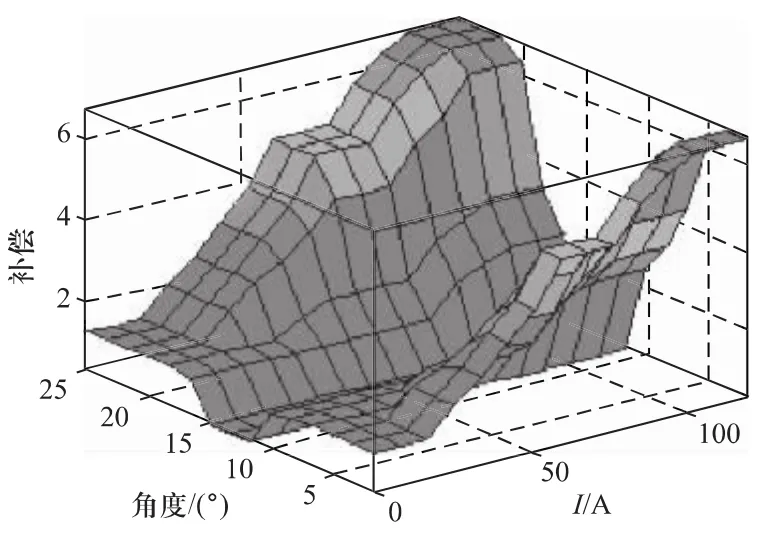
图6 模糊规则表

2.2 三相SRM仿真模型

采用的三相双闭环控制系统仿真模型，其三相模型各差15°。每相模型中，采用 MATLAB Function函数将采集到的电机位置信号(经角速度积分得到)转化为0～45°的角度值。转速环采用 PID 控制器，ki=10，kp=20，kd=0.05，电流环采用PI调节器，kp=15，ki=5。

当电机起动时，为限制起动电流，采用带模糊电流补偿的电流斩波控制，电流斩波值设置为50 A。当角速度w≥50 rad/s时，采用双闭环控制，外环速度环的输出作为内环电流环的给定，电流环的输出值送入PWM模块，与参考波形(三角波)相比较，输出占空比可调节的PWM波。

当电机制动时，首先将外环速度给定变为负值，同理，速度反馈经反相器也变为负值，这是因为制动状态下，导通角度变化，电机输出转矩为负值，为了保证闭环系统为负反馈，作此改变。倘若未改变给定与反馈方向，系统将工作在正反馈状态下。

制动状态下，当 w≥50 rad/s时，采用 PWM控制，当w＜50 rad/s时，采用电流斩波的双闭环控制。此时速度环的输出经PID调节作为电流斩波的给定值。

2.3 仿真结果

仿真结果如图7～图12所示。电动状态下速度给定值设定为w=200 rad/s，制动状态下速度给定值设定为w=60 rad/s。

由图7可知，电机可运行在电动状态下和再生制动状态下。由图11和图12相比较可知，传统控制策略下的转矩最小值为50 N·m，带模糊补偿控制的转矩最小值为80 N·m，其在一定程度上抑制了转矩脉动。

图7 转速波形

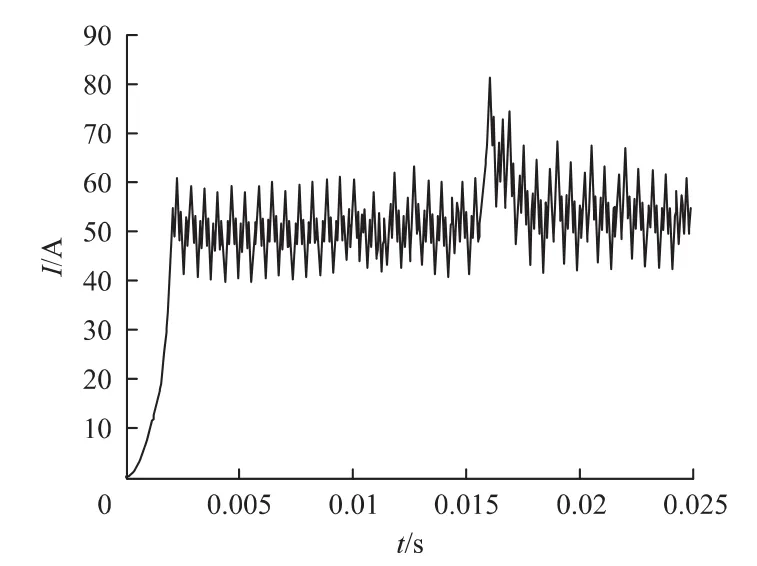
图8 斩波状态下电流波形

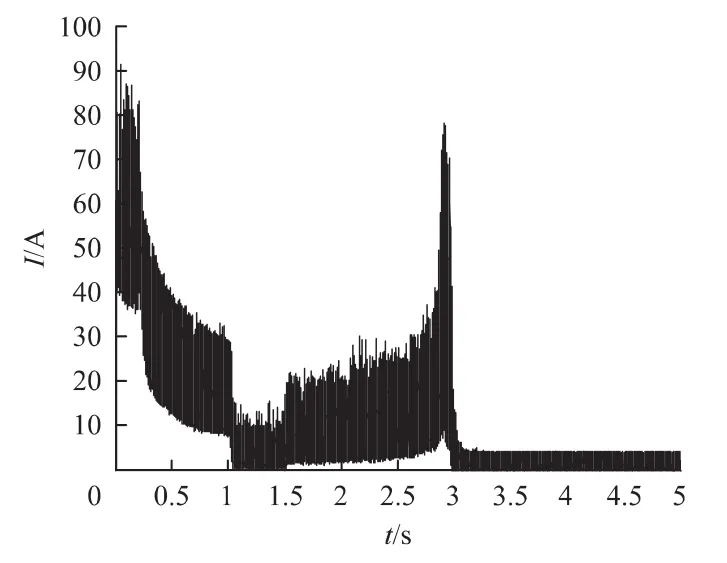
图9 三相电流波形

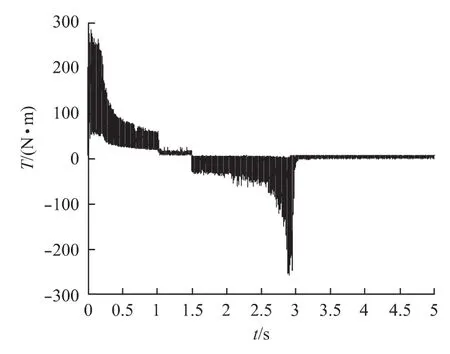
图10 三相转矩波形

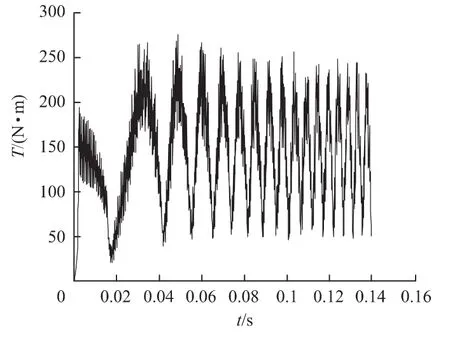
图11 传统控制下起动转矩

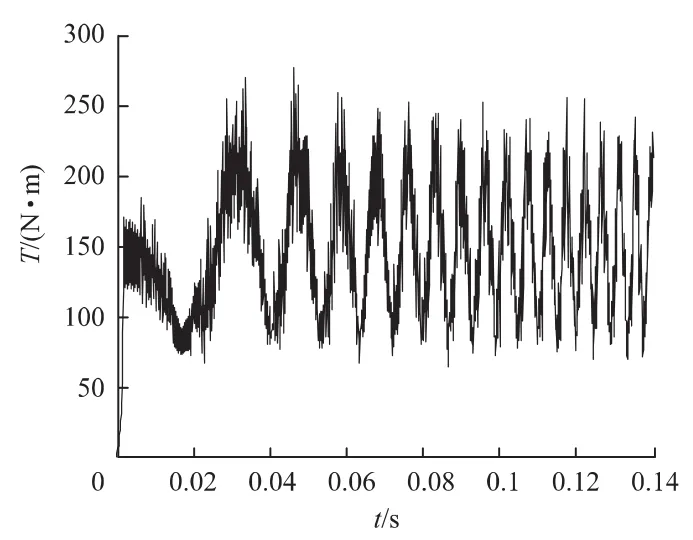
图12 带模糊电流补偿下的起动转矩

3 结语

本文针对30 kW电动汽车用外转子SRM，采用有限元分析进行了电机本体设计，较为精确地获得了SRM的静态特性。利用MATLAB/Simulink对SRM进行了系统建模和调速仿真。电动汽车用SRM要求具有较小的转矩脉动和再生制动能力。仿真结果表明本文所建立的模型和控制策略实现了再生制动的要求，且有较小的转矩脉动。结果表明SRM控制系统可以很好地应用于电动汽车领域。

[1]王宏华.开关磁阻电机调速系统控制技术[M].北京:机械工业出版社，1995.

[2]吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社，2000.

[3]吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社，2010.

[4]闫大伟.外转子开关磁阻电动机的设计及其有限元分析[D].广州:华南理工大学，2004.

[5]汤蕴璆，梁艳萍.电机电磁场的分析与计算[M].北京:机械工业出版社，2010.

[6]黄宝磊，商高高，童成前.SRM应用于混合动力汽车再生制动系统的可行性分析[J].机械设计与制造，2012，1(1):46-48.

[7]SOARES F，COSTA P J.Simulation of switched reluctance motor based on MATLAB/simulink environment[J].Aerospace and Electronic Systems，2001，37(3):989-1009.

[8]HUSAIN，EHSANIM.Torque ripple in minimization in switched reluctance motor drives by PWM current control[J].IEEE Transactions on Power Electronics，1996，11(1):83-88.