服从混合过程的金融衍生产品定价策略研究

田 军，田 晨

(1.郑州航空工业管理学院 经贸学院,河南 郑州 450015；2.英国爱丁堡大学 莫雷教育学院,爱丁堡 EH89BE,英国)

Black-Scholes期权定价模型自1973年发表以来，无论在学术界还是在实务界，都引起了强烈的反响，大大地促进了金融创新的高速发展，美国德克萨斯仪器公司还根据期权定价模型研制开发出了装有计算期权价值程序的计算器.现在几乎所有从事期权交易的经纪人都持有各家公司出品的这类计算机，利用按照这一模型开发的程序对期权交易进行估价，这项工作对金融创新和各种新型金融产品的开发与利用起到了巨大的推动作用.

随着期权交易的发展，人们逐渐发现Black-Scholes期权定价模型中一些原始假设的不合理性，并开始了修正原始模型假设条件或将模型推广到其他类型标的金融工具方面的工作.Roll[1]，Geske[2-3]和Whaley[4]运用连续时间定价的方法推出了原生证券有红利支付的看涨期权定价公式；Cox，Ross和Rubinstein[5]以及Rendleman和Barter[6]建立了离散时间期权套利定价模型——二项定价模型；Rubinstein等[7]研究了无风险价值关系，解释了看涨期权价值为什么与投资者的态度无关的原因；Merton[8]和 Levy等[9]分别讨论了期权价格的一阶随机优势边界问题；Geske和Shastri[10]研究了美式期权最优提早执行的条件；Merton[11]，Chen和Bernard等[12-13]也从不同的角度研究了金融衍生产品的定价问题.国内在相关研究方面比较落后，但最近几年也取得了很多成果[14-18].

纵观有关期权定价理论的研究文献，可见构造一个能准确、实际地估算期权价值的数学模型是相当困难的，也是每一位金融数学工作者的一项艰巨任务.为此，需要针对基于混合过程的多因素的衍生证券定价问题进行研究.

1 服从混合过程的多因素金融衍生产品定价模型

Black-Scholes期权定价模型中一个基本假设条件就是股票价格遵循ITO过程.这一假设条件虽然强调了在将来任一特定时刻股票价格的概率分布仅取决于股票当前的价格这一性质，但它只描述了股票价格在时间与空间上以连续形式的变化状态，即由经济中某些平常条件带来的正常变化，而并未反映出由经济中的不寻常情况带来的异常变化，这些不正常变化往往会引起股价大幅度的不连续跳跃.而混合过程不仅包含ITO过程，还包含Poisson跳跃过程，它既描述了由经济因素引起的股票价格的正常波动，又能准确刻画由非经济因素所导致的股票价格异常变动的特征.

现假设金融衍生市场满足：① 许将全部所得(Proceeds)卖空金融产品；②没有交易成本和税收(不付红利或其他收益)；③所有金融衍生产品是完全可分割的；④不存在无风险的套利机会；⑤金融衍生产品交易是连续的.

假若标的金融产品(或相关资产)的价格Si(i=1，2，…，n)在风险中性世界中服从如下混合过程：

(1)

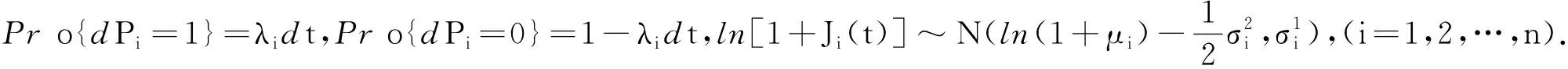
为建立基于混合过程多因素衍生金融产品价格所满足的微分方程，先给出几个引理.

(2)

利用一元函数的泰勒公式及多元复合函数求导法则，便可得到式(2).

引理2 设状态变量xi遵循下列ITO过程

(3)

则对任意f=f(x，t)，有

(4)

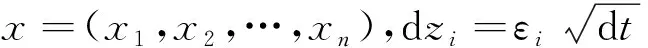
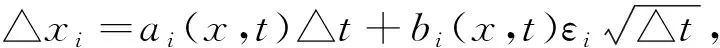
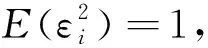
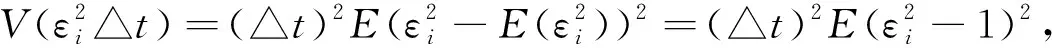
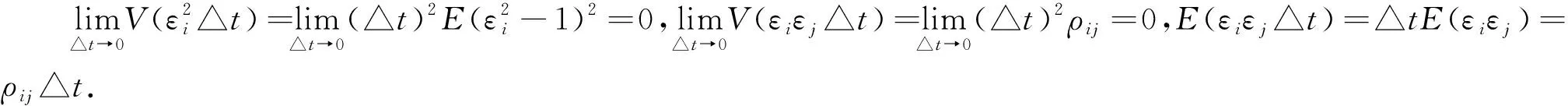
根据引理1得(4)式.

定理设标的金融产品的价格Si在风险中性世界中服从式(3)中的混合过程，f(S，t)是依赖于标的金融产品Si的衍生金融产品的价格，r表示瞬间无风险利率，ρij表示dzi与dzj之间的相关系数(1≤i，j≤n)，则

(5)

其中，θi(1≤i≤n)是仅依赖于状态变量S与时间t的常数，Ki(t)是Poisson过程△Pi的振幅，S=(S1，S2，…，Sn)，Ei(S，t)=λiE[f(S1(1+J1)，S2(1+J2)，…，Sn(1+Jn)，t) -f(S1，S2，…，Sn，t)].

证明根据引理1和引理2，结合(3)的表达式可得

(6)

式中，只有含项dzi是随机项.

为消除随机项，构筑无风险金融衍生产品组合G，并假定Fk具有相同于f的扩散过程(6)，定义hk为第k个金融产品在证券组合中的投资份额，则

(7)

选择hk，使得金融产品收益率中的随机分量项为0.根据方程(6)可知：

(8)

因此，金融产品组合的收益

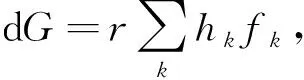
(9)

方程(8)与方程(9)可视为包含hk的n+1个线性方程组：

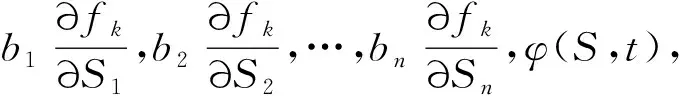
令fk=f的，整理得

(10)

其中,θi(1≤i≤n)是仅依赖于状态变量Si(1≤i≤n)与时间t的常数.

方程(10)即为服从混合过程的多因素衍生金融产品的价格所满足的二阶偏微分方程.

特别地，若Pi(t)=0(i=1，2，…，n)，则Ki(t)=0(i=1，2，…,n),此时方程(10)成为一般形式多因素衍生金融产品价所满足的微分方程.

2 衍生金融产品定价模型分析

现在利用多因素衍生金融产品定价模型来讨论股票价格与利率之间以及依赖它们的衍生金融产品价格间的关系.

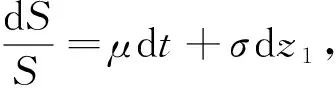
假定利率r也遵循某种关于时间t的随机过程，它满足如下ITO过程：

dr=a(r，t)dt+b(r，t)dz2，

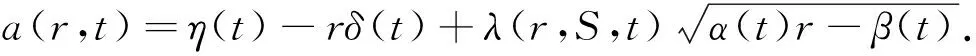
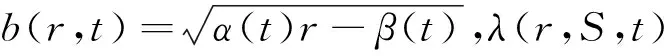
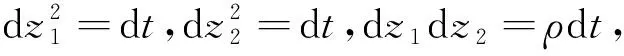
假若衍生金融产品的价格f由股票价格S、利率r及时间t决定，则由定理结论知

(11)

其中,ω(r，S，t)=a(r，t)-b(r，t)λ(r，S，t)=η(t)-rδ(t),表示一类额外的市场风险，它仅取决于标的变量r,S和时间t，而与证券的性质无关.

这也说明，Black-Scholes期权定价方程是基于混合过程多因素衍生金融产品定价模型的一个特例.

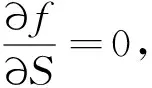
(12)

值得注意的是，方程(12)能较好地验证 Ho和Lee所建立的有关面值为S0的零息票普通债券定价模型

f(r，t)=S0eA(t，T)-rB(t，T).

(13)

将式(13)代入方程(12)，有

(14)

对式(14)进行两次关于r的微分，可得到

因为B是关于T的函数，而a(r，t)，b(r，t)，λ(r，t)与T无关，所以

(15)

从a(r，t)，b(r，t)的表达式不难看出，方程(15)恒成立.

年龄通过了显著性检验，说明年龄对外出务工意愿具有显著影响。年龄系数值为0.915，其实际意义为年龄每增大1年，其外出意愿为原来的0.915倍。0.915小于1，表明年龄越大，劳动力外出务工的意愿越小。青壮年劳动力的视野更开阔，对就业收入、行业及机会等有更高要求，被城镇更多的就业机会、更高的劳动报酬所吸引，从而外出务工意愿更强烈。

3 衍生金融产品定价模型的求解方法

基于混合过程的多因素衍生金融产品定价模型的解，是求解n+1元二阶偏微分方程问题，对这样一个二阶偏微分方程求解是相当困难的.为此，仅讨论基于两种标的证券的衍生金融产品的定价模型，至于两个以上标的证券的多因素衍生金融产品的定价问题，可仿效求之.

设两种标的证券的价格S1和S2在风险中性世界中遵循如下几何Brownian运动：

dS1=a1(S1，S2，t)dt+b1(S1，S2，t)dz1，
dS2=a2(S1，S2，t)dt+b2(S1，S2，t)dz2，

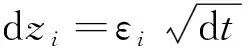
设依赖于标的证券S1和S2的衍生金融产品价格为f=f(S1，S2，t)，则由泰勒展开式知

其中,ρ是dz1与dz2间的相关系数.

因此，当无风险利率为r时，根据无套利原则，有dG=rGdt,即

(16)

若b1=σ1S1，b2=σ2S2(σ1、σ2为常数)，则方程(16)变成为

(17)

为求满足方程(17)的衍生金融产品的价格f(S1，S2，t)，不妨设定f(S1，S2，t)的终期收益为f(S1，S2，t)=max(S2-S1，0).

则方程(17)的约束条件为s.t.f(S1，S2，t)=max(S2-S1，0).

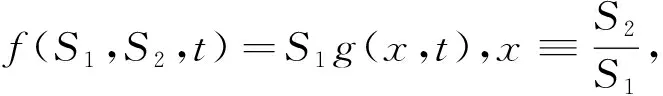
从而方程(17)可化简为

(18)

且约束条件变为

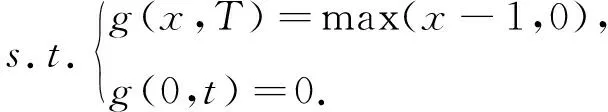
(19)

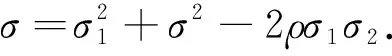
g(x，t；T)=c(x，t；T),

所以

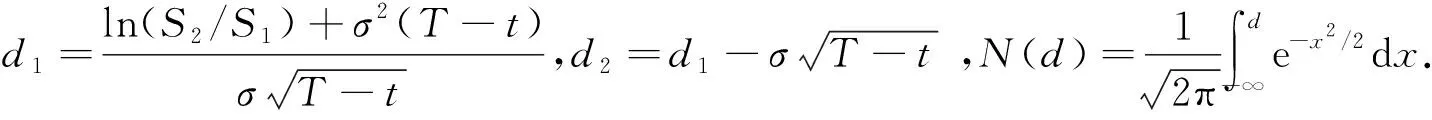
4 结束语

衍生金融产品定价的理论与方法一直是学术界与实务界较为关注的热点问题.在金融市场，金融衍生产品具有很强的变化流动性和转移收益/风险的特性，金融衍生产品的价格都受一种不确定因素的影响.本研究中所建立的基于混合过程的多因素衍生金融品定价模型只是从一个侧面给出了标的证券服从混合过程时衍生金融产品的定价方法，也是对Black-Scholes期权定价公式的推广.

参考文献：

[1] Roll R.An analytic formula for unprotected American call options on stocks with known dividends[J].Journal of Financial Economics, 1979 (7): 375-380.

[2] Geske R.A note on an analytic valuation formula for unprotected American call options on stocks with known dividends[J].Journal of Financial Economics, 1979(7): 375-380.

[3] Geske R.The valuation of compound options[J].Journal of Financial Economics, 1979 (7): 63-81.

[4] Whaley R.Valuation of American futures options:theory and empirical tests[J].Journal of Finance, 1986 (41): 127-150.

[5] Cox J C,Ross S A,Rubinstein M. Option pricing:a simplified approach[J].Journal of Financial Economics, 1979: 229-263.

[6] Rendleman R,Barter R.Two-state option pricing[J].Journal of Finance,1979(12):1093-1110.

[7] Rubinstein M.he valuation of uncertain income streams and the pricing of options[J].Bell Journal of Economics,1976(8):407-425.

[8] Merton R.On the pricing of corporate debt: the risk structure of interest rates[J].Journal of Finance,1973(2):449-470.

[9] Levy H.Upper and lower bounds of put and call option value:stochastic dominance approach[J].Journal of Finance,1985(9):1197-1217.

[10] Geske R,Shastri K.The early exercise of American puts[J].Journal of Banking and Finance, 1985 (9): 207-219.

[11] Merton R. The relationship between put and call option prices:comment[J].Journal of Finance, 1973 (28): 183-184.

[12] Chen W. An extensive exploration of three key quantitative approaches for pricing various hnancial derivatives[D].New South Wales: University of Wollongong, 2011: 219-262.

[13] Bernard C,Boyle P.Montecarlo methods for pricing discrete parisian options[J].European J Finance,2011(17):169-196.

[14] 田军,黄登仕,郭耀煌.多因素证券组合投资最优决策的加权集成方法[J].系统工程理论与实践, 2001(8): 87-91.

[15] 郭冬梅,宋斌,汪寿阳.倒向随机微分方程与巴黎期权的非线性定价[J].中国科学: 数学,2013,43(1):91-103.

[16] 吴鑫育,杨文昱,马超群,等.基于非仿射随机波动率模型的期权定价研究[J].中国管理科学,2013,21(1):1-7.

[17] 袁缘,张诚斌,李辉来.基于跳扩散过程的一类期权定价模型[J].吉林大学学报理学版,2013,51(2):187-190.

[18] 邓英东,肖庆宪.跳扩散模型下股价服从几何布朗运动的Esscher变换定价[J].数学的实践与认识,2013,43(12):76-80.