基于支持向量机的桥梁群体震害预测方法
谭 潇, 杜 鹏, 孙作玉
(1.广州大学,广东 广州 510006;2.广东省地震局,广东 广州 510070)
引言
桥梁是城市生命线系统中交通网络的重要组成部分,是保证城市交通功能正常运行的基础。强烈地震后,如果桥梁出现严重破坏,将会对整个交通系统造成极大的影响,从而给人们的正常生活以及震后的抗震救灾工作造成极大的障碍。因此,研究桥梁的震害,对震后桥梁的破坏等级做出科学合理的预测,具有极大的现实意义。
经过国内外专家近几十年的分析研究,目前用于评估桥梁震害的方法[1、2]有很多,其中桥梁群体震害预测中使用最广泛的为朱美珍的 “经验统计法”[3],其需要的参数容易确定,无需复杂的运算,在一定概率范围内可预测桥梁易损性,而且准确率相对较高。近些年来,BP神经网络多次被运用到群体桥梁震害预测中[4],但是由于其本身的一些局限性,存在一些不足:①可能会陷入局部极小而无法找到全局最优解;②收敛速度慢;③可能会产生“过学习”问题。
本文基于SVM的机器学习方法,利用LibSVM工具箱,建立了一种新型的桥梁群体震害预测方法,它能有效改善神经网络的上述问题,更加科学、高效的对桥梁进行震害预测。
1 支持向量机的原理
支持向量机(Support Vector Machines,简称SVM)[5]是Cortes和Vapnik于1995年提出的,它在解决小样本、非线性和高维模式识别中具有很多特有的优势,并且能够推广应用到函数拟合等其他机器学习问题中。
支持向量机方法是建立在统计学习理论[6]的VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度,Accuracy)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳平衡,以期获得最好的推广能力。
SVM是从线性可分情况下的最优分类面发展而来的,其基本思路可以通过图1所示的二维情况来进行说明。

图1 最优分类面示意图Fig.1 Sketch map of the optimal classification face
图1中,C1和C2分别表示要区分的两类数据样本,H表示分类线y=ux+b,H1和H2是平行于H,且过离H最近的两类样本的直线,H1与H,H2与H之间的距离就叫做几何间隔,表达式为:

所谓最优分类线就是不但能将两类数据样本正确的分开,使训练错误率最小,而且还要使几何间隔最大。前者保证经验风险最小;而后者实际上就是使推广界中的置信范围最小,几何间隔越大的解,其误差上界就越小。由二维空间拓展到高位空间,最优分类线就成为了最优分类面。相应的分类问题可以转化成一个带约束的求最小值问题,其数学表达式如下:


由式(2)可见,该问题为一个带不等式约束的优化问题,可以通过添加Lagrange乘子,构造Lagrange函数解决此问题,并最终将上述最优分类面的求解问题转化为如下凸二次规划寻优的对偶问题:

(3)式中,ai为对应的Lagrange乘子;K(xi,xj)称为核函数,它可以实现由低维空间到高维空间的映射,从而解决非线性问题,常用的核函数有多项式函数、径向基函数和Sigmoid函数等[7]。在对上面的最优化问题进行求解后[8],即可得到最优分类面函数:

2 模型建立
2.1 输入输出参数
本文选择了吴昊[9]统计的唐山大地震、通海地震、海城地震、丽江地震、台湾集集地震、汶川地震中103座桥梁的震害情况,随机选取其中83个样本用于进行学习训练,剩余的20个样本作为测试检验。输入的样本参数为与桥梁震害相关的各个因素的量化值,鉴于城市交通桥梁的特点,吴昊改进了朱美珍经验公式中考虑的9个影响因素[3],修改后的影响城市桥梁震害的主要因素及其量化值见表1。

表1 震害因素及其量化值Tabel 1 Damage factors and quantitative value
桥梁的震害程度一般可以分为五种[10],五种破坏等级分别为:完好(Ⅰ)、轻微破坏(Ⅱ)、中等破坏(Ⅲ)、严重破坏(Ⅳ)和毁坏(Ⅴ)。将桥梁的破坏等级作为输出参数,其对应的量化值分别为1、2、3、4、5。
2.2 建模步骤
LibSVM[6]是台湾大学林智仁(Lin Chih-jen)等开发设计的一个简单、实用且快速有效的SVM模式识别与回归的软件包。利用该工具箱可以解决C-SVM分类、υ-SVM分类、ε-SVM回归和υ-SVM回归等问题。在准备好输入输出的样本参数后,利用LibSVM工具箱可以建立SVM模型:
(1)由于所要解决的问题属于分类问题,因此设置SVM类型为C-SVM。
(2)核函数选择普遍使用的径向基函数,其表达式为:

因为它对应的特征空间是无限的,数据样本在该特征空间中肯定是可分的,而且不会出现太大的偏差。
(3)通过实验对比的方式,选择的惩罚因子C和核函数的参数gamma的数值分别为9和3。
(4)对83个训练样本进行训练获得支持向量机模型。
(5)利用得到的模型对20个测试样本进行测试与预测。
3 预测结果与实际结果比较
针对上述的SVM模型本文采用Matlab R2001b,借助LibSVM工具箱进行编程,从而得到20个测试样本的预测结果,并与实际结果进行了比较。同时采用BP神经网络对20个测试样本进行了预测,且与实际结果进行比较。两个对比图分别见图2和图3。

图2 SVM预测结果与实际结果对比Fig.2 Comparison of the predicted results by SVM and the actual results
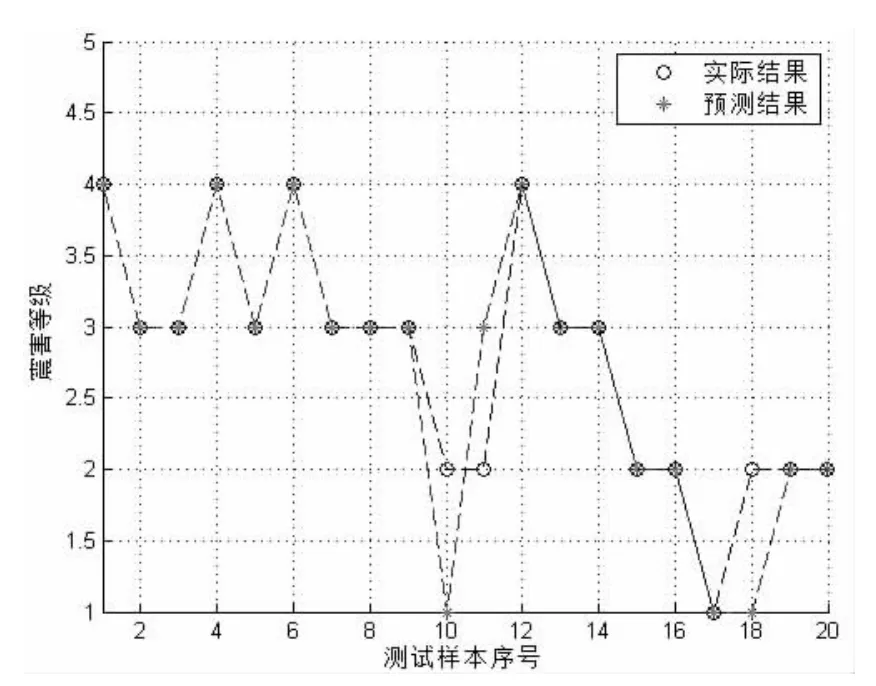
图3 BP预测结果与实际结果对比Fig.3 Comparison of the predicted results by BP and the actual results
从图2、图3中可以看到,SVM模型预测得到的结果仅有10、18两座桥梁与实际结果不一致,其原因是训练样本库中输出结果为1的样本数量太少导致数据集偏斜,使10、18两座桥梁被错分,可以通过均匀分布各样本来改善;而BP模型预测得到的结果有10、11、18三座桥梁与实际结果有差异,另外BP模型每次的预测结果并不稳定;从时间上进行对比,SVM模型的运算时间仅为3 s,而BP模型的运算时间却达到41 s。经过多次仿真分析,均验证了上述的结论,说明SVM模型具有更好的推广能力,而且更高效,可以应用于实际的震害预测工作中。
4 结语
本文应用SVM的机器学习方法在城市桥梁震害预测方面进行了研究,给出了一种科学高效的评估方法,并且验证了评估结果的准确性。它具有坚实的理论基础和严格的数学推理,而且具有以下优点:①很少出现过拟合;②对于特征过多造成维数灾难不明显;③不会收敛于局部最优解,即其收敛解是全局最优解;④预测结果相对稳定可靠。
尽管SVM算法法存在很多的优点,但是,到目前为止,该方法在实际应用中仍存在一定的不足:
(1)参数的选择没有统一的模式。尽管可以运用程序中的交互检验功能来进行寻优,但有时寻找出来的参数并不能得到较高的准确率,这就需要我们使用实验对比来寻找最佳参数,给预测工作带来了一定的困难。
(2)仅适用于中小规模样本系统。由于SVM是借助于二次规划来求解支持向量,而求解二次规划涉及到m阶矩阵的计算(m为样本数目),当样本数目很大时,矩阵的存储和计算都将耗费大量的机器内存和运算时间。在桥梁的震害评估中,一般不会涉及到规模庞大的数据量计算,因此不存在此问题。
[1]王东升,翟桐,郭明珠.利用Push-over方法评价桥梁的抗震安全性[J].世界地震工程,2000,16(2):47-51.
[2]王东升,冯启民.桥梁震害预测[J].自然灾害学报,2001,10(3):113-118.
[3]朱美珍.公路桥梁震害预测的实用方法[J].同济大学学报,1994,22(3):279-283.
[4]赵钊,郭恩栋,王再荣,等.基于人工神经网络的城市桥梁震害评估方法[J].世界地震工程,2011,27(4): 7-12.
[5]Cortes C,Vapnik V.Support vector networds[J].Machine Learning,1995, 20: 273-295.
[6]Vapnik V N.The Nature of Statistical Learning Theory[M].New York: Springer Verlag, 1995.
[7]白鹏,张喜斌,张斌,等.支持向量机理论及工程应用实例[M].西安:西安电子科技大学出版社,2008.
[8]J C Platt.Using Analytic QP and Sparseness to Speed Training of Support Vector Machines[M].Cambrige:MIT Press.1999.
[9]吴昊.城市轨道交通桥梁震害预测方法研究[D].北京:北京交通大学,2009.
[10]国家质量监督检验检疫总局.GB/T 19428-2003,地震灾害预测及其信息管理系统技术规范宣贯教材[M].北京:中国标准出版社,2004.

