煤矿用钻装机挖臂机构动力学仿真分析

唐 娟，杨 林，2

(1.中煤科工集团重庆研究院， 重庆 400039;2.瓦斯灾害应急信息技术实验室， 重庆 400039)

0 引言

随着经济的高速发展，煤矿安全高效生产越发重要。煤矿巷道用全液压钻装机可以代替耙斗装岩机和液压台车实现岩石巷道掘进除渣和凿岩钻孔作业，在提高生产效率的同时减少了安全隐患。钻装机主要是由扒渣工作装置(挖臂)、凿岩推进工作装置(钻臂)、刮板运输机组成，其中挖臂是由水平摆动座、动臂、斗杆、四杆机构以及扒斗5个部分串联而成(如图1所示)，是钻装机中关键的工作部件，其作业效率决定了钻装机的装载性能。

钻装机除渣作业依赖于挖臂各个部件之间的相对转动。对挖臂进行动力学分析和建模是完成挖臂结构设计和实现挖臂运动控制所必需的。挖臂是由多个转动关节串联而成，是由多个刚体组成的动力学系统，具有非线性以及多输入、多输出的特点，各个部件之间存在着复杂的耦合关系。为了使挖臂完成预期的作业路径，每个关节必须提供一定规律的驱动力矩。

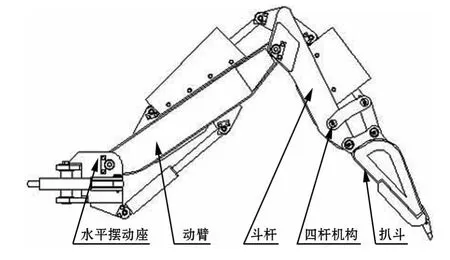
图1 挖臂结构

通过建立挖臂机械手的动力学模型，并对机械手动力学模型进行分析与评价，可为得出合理的结构尺寸以及恰当的驱动油缸参数提供数据基础。

1 挖臂作业轨迹空间

挖臂的作业空间范围与挖臂上各个转动部件的结构尺寸以及驱动油缸的参数有关，通过调整动臂、斗杆、扒斗以及四杆机构的结构尺寸以及相对应的驱动油缸参数(缸筒尺寸、缸杆尺寸、流量等)，可以得到不同的作业空间范围。为了计算扒斗斗齿在基础坐标空间内的活动范围，在每个转动部件上固结一个坐标系，然后描述这些坐标系之间的变换关系，通过这些变换关系，最终计算出斗齿的活动空间。为此，引入D－H(Denavit－Hartenberg)变换，利用一个4×4的齐次变换矩阵，表示两个相邻坐标系的变换关系，齐次变换矩阵可描述为下面的形式:

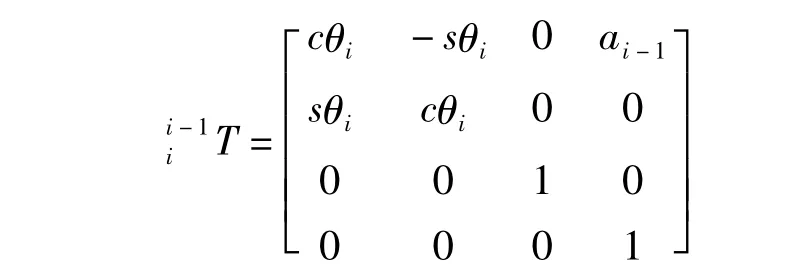
s——正弦函数 sin();

c——余弦函数 cos();

θi——两个部件之间的关节角;

ai－1——两部件关节间的长度，即相邻坐标系原点间的距离。

齐次变换矩阵可以写成如下形式:

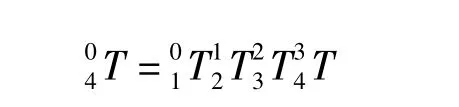
挖臂各个部件的参数如表1所示。

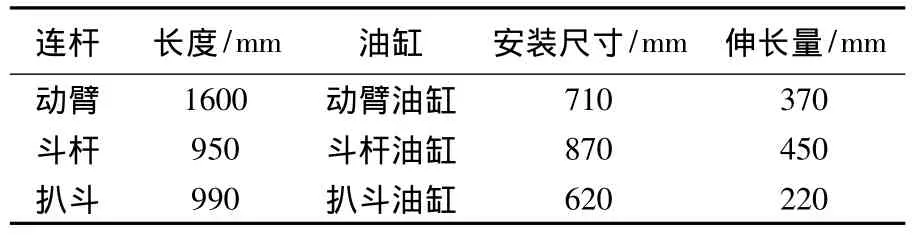
表1 构件参数表

利用上述公式，将斗齿尖所能达到的空间位置在Matlab软件中描述出来，得到扒斗斗齿的作业空间包络图如图2所示。

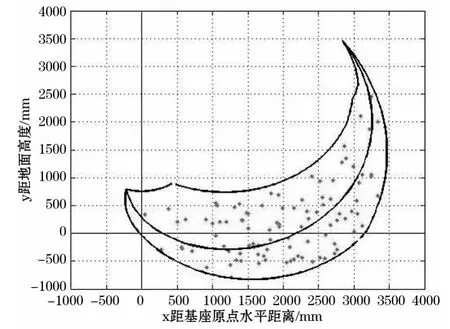
图2 斗齿活动空间包络图

2 动力学分析

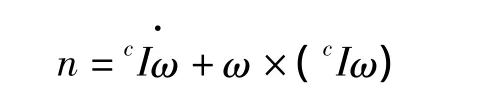
规定坐标系{c}的坐标原点为刚体的质心，相对于坐标系{c}，惯性张量cI定义为3×3的对称矩阵:

式中，对角线元素是刚体绕三坐标轴x，y，z的质量惯性矩:

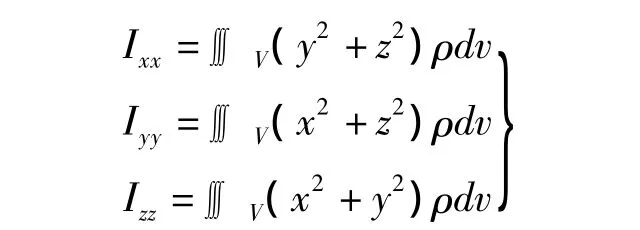
其余元素的惯性积:

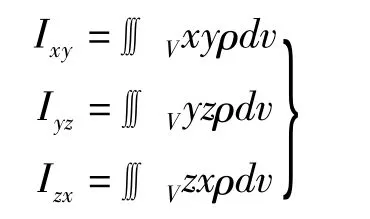
式中，ρ——结构件的密度;

挖臂斗齿的运动速度可以由两部分组成:扒斗坐标系坐标原点的速度和加速度，以及扒斗相对于扒斗坐标系的角速度和角加速度。vi和ωi分别表示挖臂的各个部件坐标系{i}相对于基座坐标系{0}的速度，ivi和iωi则说明vi和ωi在本部件坐标系{i}中表示的线速度和角速度，同理i+1vi+1和i+1ωi+1表示在部件坐标系{i+1}中的线速度和角速度。

部件i+1相对于部件i的角速度是绕转动关节i+1运动引起的。

在相同坐标系中，两个向量可以相互叠加，因此部件i+1的角速度等于部件i的角速度加上部件i+1绕关节i+1转动的角速度，在{i}中的表示为:

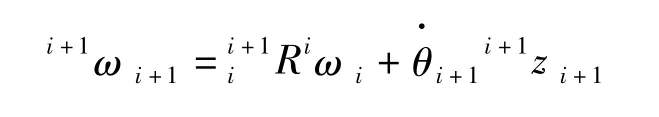
坐标系{i+1}原点的线速度等于坐标系{i}原点的线速度加上部件i因转动而产生的速度分量，ipi+1表示{i+1}坐标原点在坐标系{i}中的位置矢量，因此得到速度公式:

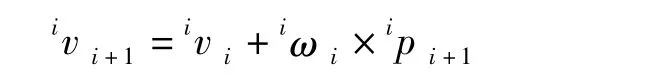
19世纪中叶，统计学形成了两个主要的学派，数理统计学派与社会统计学派．随着概率论的成熟，为统计学的发展奠定了数学基础．19世纪中叶，比利时的阿道夫·凯特勒（1796—1874）主张用自然科学的方法研究社会现象，把古典概率论引入了统计学，使得统计学进入了一个新的发展阶段．不过凯特勒将自然科学的观点与方法机械套用到犯罪、道德等社会问题，混淆了自然现象与社会现象之间的本质区别．尽管如此，凯特勒把概率论引入统计学至少使得统计学在“政治算术”的“算术”方法基础上往准确化道路迈进了一大步，他为后期数理统计学的形成与发展奠定了基础．

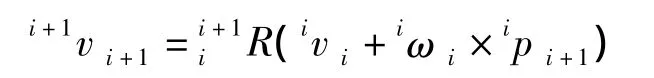
分别对上述公式求微分，即可得出各个部件的角加速度和线加速度的传递公式:

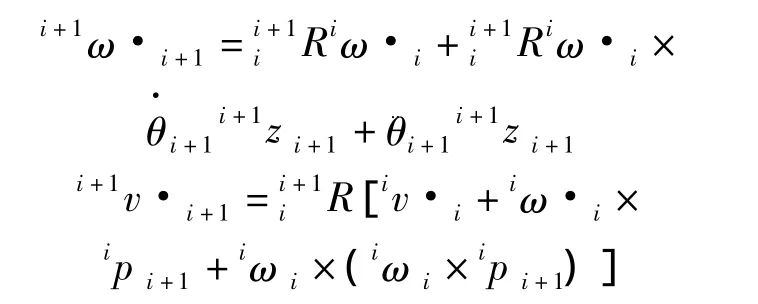
同理，求出部件质心的加速度为:

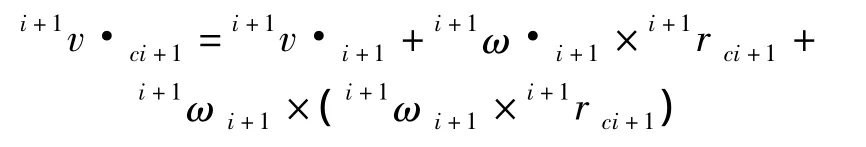
根据牛顿－欧拉方程得出挖臂各个部件之间的力、速度关系通式:

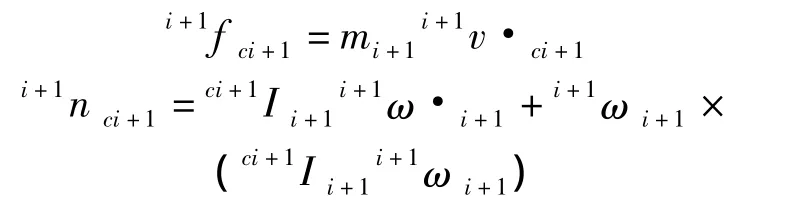
对挖臂进行静力学分析时，首先对其中一个部件进行受力分析，从而建立部件的静力学平衡方程。当部件处于力学平衡状态时，所受到的合力以及合力矩为零。推导出力和力矩的平衡方程为:

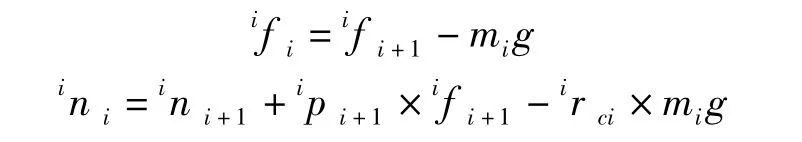
式中，ifi，ini——部件 i受到部件 i－1 的作用力、力矩;

由于{0}固结在水平摆动座上，在x，y平面内，是固定不动的，因而0ω0=0，0v0=0，{4}固结在扒斗的末端，即斗齿尖的位置，得出θ4=0=0。

挖臂运动具有多输入、多输出的特点。由于输入参数的不同，在相同的位置点也会产生不同的速度以及挖掘力。为了更清楚的描述挖臂的速度、力参数与斗齿所在的位置之间的关系，选取一个工作路径，并分析这个工作路径上所有连续点的速度以及挖掘力曲线并利用Matlab分析其数据曲线(如图3～图4所示)。

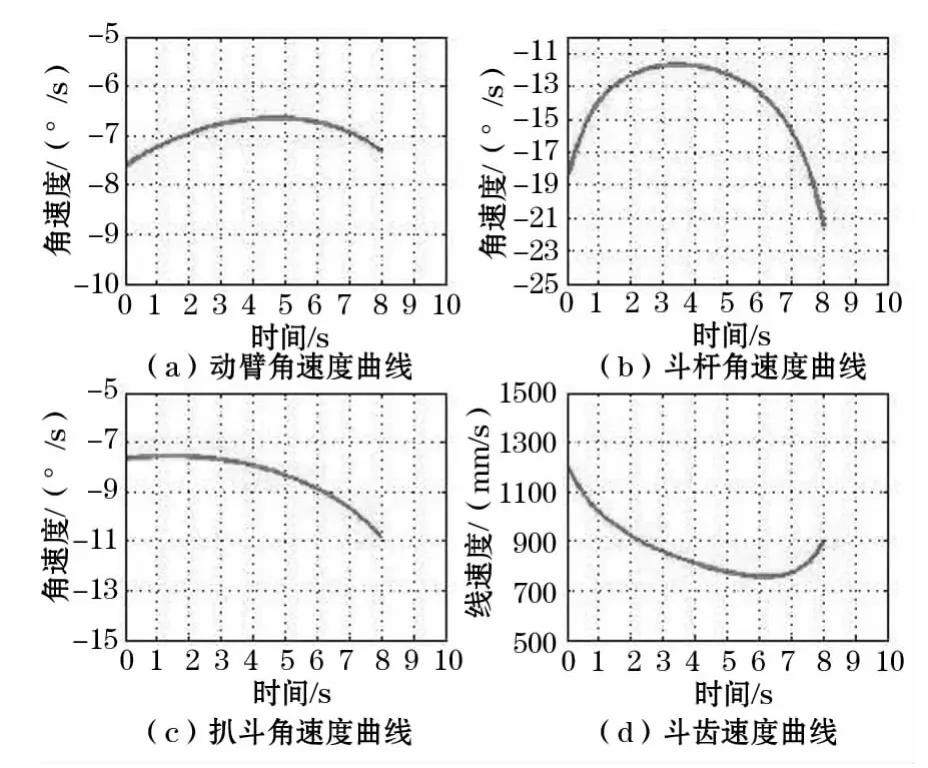
图3 挖臂速度曲线

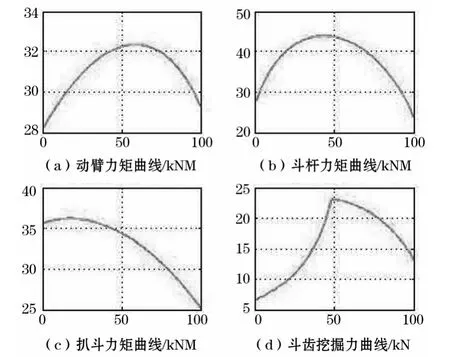
图4 挖臂挖掘力曲线

3 动力学性能优化

在奇异点挖臂会丧失一个或者几个自由度。在奇异点附近，其动力学性能也会变差;离奇异点越远，挖臂在各个方向的运动性能和施力效果的一致性愈好。挖臂的动力学性能，对于挖臂结构设计、工作空间选择、控制方案拟定、液压系统选型以及轨迹规划都具有十分重要的作用。挖臂动力学的复杂性不仅在于结构复杂性，还在于煤矿井下除渣作业情况的多样性和影响因素的可变性。在设计挖臂工作范围或实现挖臂轨迹控制时，最值得注意的是一些最严峻最危险的情况，如最高速度作业时，最大关节驱动力时，挖臂悬伸最长时等，应该考虑这些最坏情况下的作业情况和对动力学的要求。因此，提出了衡量挖臂动力学性能的综合性能指标以及相应的优化方法。为了说明各种动力学性能指标之间的联系，根据H.Asada的广义惯性椭球GIE(generalized inetia tensor ellipsoid)理论来评定挖臂的动力学特征。广义惯性椭球理论GIE实质上是以笛卡尔惯性矩阵的特征值来描述挖臂在各个方向上的加速特征:

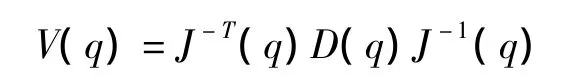
式中，D(q)——操作臂的惯性矩阵，可以通过推导公式求出;

J(q)——雅克比矩阵。

对于n×n的惯性矩阵V(q)，二次型方程:

可以表示n维空间中的一个椭球，称之为广义惯性椭球GIE。惯性矩阵V(q)特征矢量的方向即为椭球的主轴方向，矩阵V(q)特征值的平方根为椭球主轴的长度。利用广义惯性椭球GIE来衡量挖臂的加速性能具有明显的几何直观性。在挖臂斗齿的活动空间内的任何一点，根据上述二次型方程可以画出一个椭球，该点对应椭球的形状可以衡量其动力学性能的好坏，椭球愈接近球，即主轴长度一致时，动力学性能愈好。广义惯性椭球的形状完全是个圆球的点称为动力学各向同性点，在动力学各向同性点上，惯性矩阵V(q)的列向量互相线性独立，并且模相等。椭球接近于圆球形时，加速性能变好，近似于各向同性;在工作空间边缘部分，椭圆变扁，动力学性能变差，图5为钻装机挖臂部分空间位置的广义惯性椭球图。

4 结论

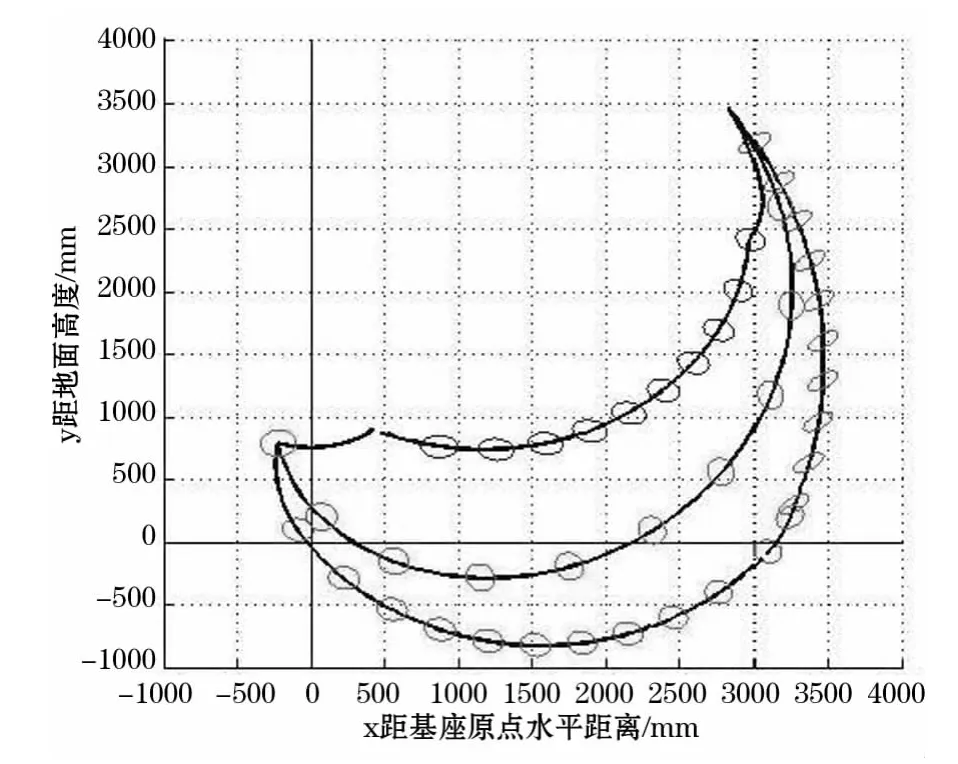
图5 挖臂空间惯性椭球图

基于D－H法，建立两个相邻部件之间的空间变换关系，并以此推导出斗齿在基础坐标系内的活动范围，做出斗齿的工作空间包络图。利用牛顿－欧拉方程建立挖臂的动力学方程，并借助MATLAB软件进行动力学仿真计算，得出动臂、斗杆、扒斗的驱动力矩变化规律，分析出斗齿末端的速度、力曲线。最后利用广义惯性椭球理论，评价挖臂在整个工作空间的动力学性能，为挖臂的机械结构设计、工作空间的选择、作业轨迹规划和控制方案的拟定提供数据参考。

［1］熊有伦，丁 汉.机器人动力学性能指标及其优化［J］.机械工程学报，1989，25(2):9-15.

［2］Asada H.A Geometrical Represantation of Manipulator Dynamics and its Application to Arm Design［J］.Trans.Of ASME J.Optimiation of Dynamic Systems，Measurement and Control，1983，105(3):140-145.

［3］John J.Craig.Introduction to Robotics Mechanics and Control Third Editoin［M］.London:Pearson Education Ltd，2005.

［4］杨 武，蒋梁中.采用牛顿－欧拉法的排爆机器人机械手动力学分析［J］.现代制造工程，2010(6):140-143.

［5］黄 真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006.

［6］任晓华，任运涛.钻装机耙渣工作装置运动学仿真分析［J］.煤矿机械，2012，33(4):69-71.