天然连续弯道中水流运动的三维数值模拟

吕岁菊，冯民权，李春光

(1.西安理工大学 陕西省西北旱区生态水利工程重点实验室，陕西 西安 710048;2.北方民族大学 土木建筑工程学院，宁夏 银川 750021)

对弯道水流运动规律的研究，在水利工程的许多领域占有重要的位置，研究成果在河流治理、港口兴建、引水防沙以及改善河道航运等方面都得到广泛的应用［1］.连续弯道的水流特性影响着弯道泥沙运动和河床演变的基本规律，是河流动力学研究的主要问题之一.因此，认识河流弯道的水流结构，准确地模拟弯道处水流特性尤其重要.

河流弯道处水流会出现表面流指向凹岸，底流指向凸岸的螺旋流(环流)结构，环流运动引起的横向输沙，使弯道呈现出凸岸淤长，凹岸冲蚀的现象，泥沙在横向上的输移作用对河床冲淤非常明显，而平面二维数学模型不能处理次生环流问题.次生环流对污染物、泥沙运动及河床变形起着关键作用，因此，随着计算机速度的提高和存储量的增大，三维数学模型得到迅速发展［2－7］.在网格划分、紊流模型选取、壁面边界条件处理、计算程序优化等方面也取得了进步，尤其是以SIMPLE算法结合k－ε紊流模型的数值模拟发展已比较成熟.文献［8］建立了非正交曲线坐标下弯曲河流的标准k－ε紊流模型对弯曲河流进行了三维模拟.文献［9］采用带旋流修正的紊流模型对连续畸弯的水流运动进行了数值模拟研究.文献［10］利用标准k－ε紊流模型对室内90°弯道水流运动进行了三维数值模拟.但对天然连续弯道而言，由于受诸多因素的影响，三维水流的模拟还处于起步阶段.本文在对标准k－ε模型分析的基础上，考虑时均应变率对Reynolds正应力及紊动动能对ε方程有较大影响，基于上述原因，为了能使模拟结果更符合天然连续弯道的实际情况，对标准k－ε模型进行了改进.

本文模拟区域为天然河道，形状极不规则，采用适体坐标变换将笛卡尔坐标系下三维Reynolds应力方程变换到计算坐标ξ－η－ζ下.针对天然弯曲河流，由于弯道螺旋流和水面比降的影响，水面沿程变化较大.首先通过实测水位插值得到计算节点上的水位，用这一水位作为计算区域的表面，采用“刚盖”假定近似自由水面.利用有限体积法离散方程，变量布置采用同位网格，将u，v，w，k，ε布置在同一个网格节点上，并运用SIMPLEC算法进行求解.

1 数学模型

1.1 三维紊流水流控制方程

Navier-Stokes方程是描述流体运动最基本的方程组，考虑水流紊流的随机脉动，则不可压水流运动的连续性方程和动量方程为:

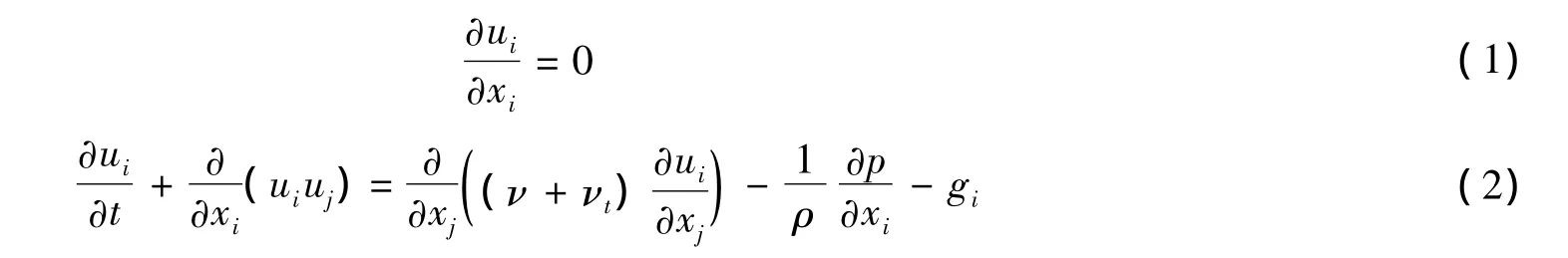
式中:下标 i，j=1，2，3，遵循求和约定;u1，u2，u3分别为 x，y，z方向的 Reynolds时均流速.

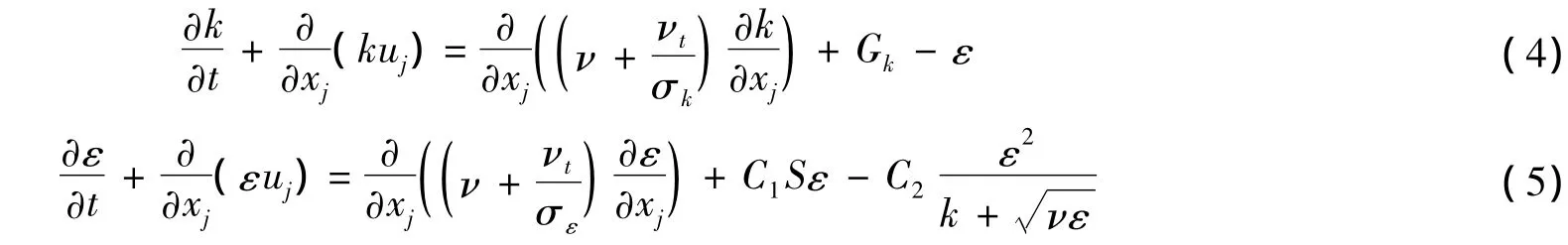
1.2 适体坐标下紊流水流模型

由于天然河流边界曲折，地形复杂，对式(1)～(5)采用适体坐标变换，从物理区域(x，y，z)变换到计算域(ξ，η，ζ)，其统一形式为:

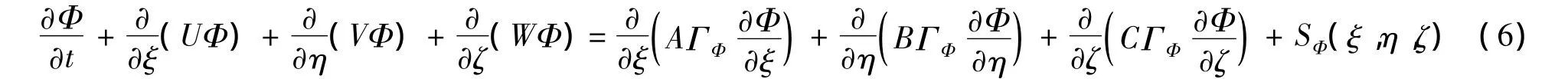
表1 适体坐标系下通用控制方程中的变量、系数和源项Tab.1 Variable，coefficients and source item of governing equations in body-fitted coordinate

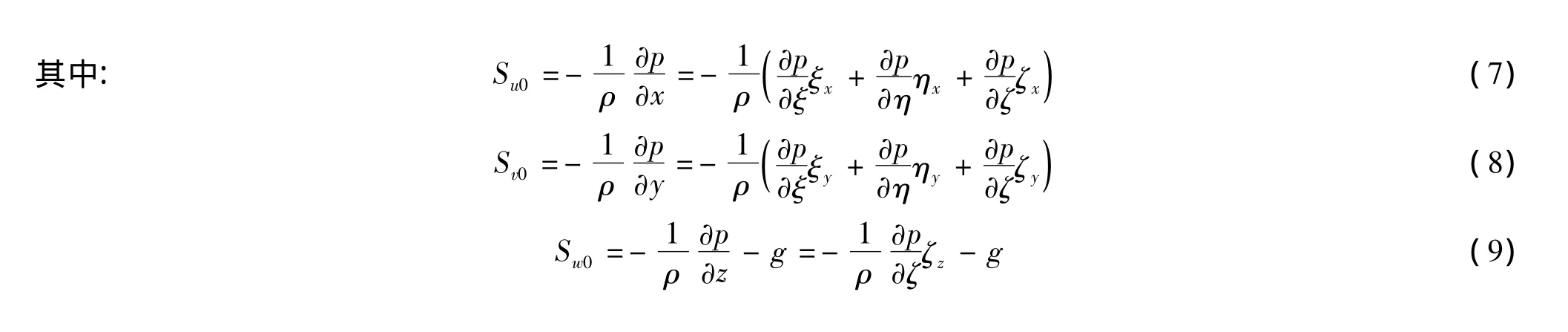
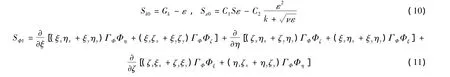
2 数值模型

2.1 控制方程的离散

采用有限体积法对式(6)进行离散，非恒定项采用隐式差分格式，对流项采用迎风格式，扩散项采用中心差分格式，源项采用线性化处理的方法，其离散形式为:

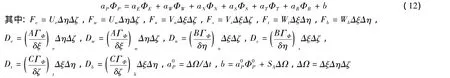
2.2 定解条件

固壁边界采用无滑移条件，并由壁面函数法处理［14－15］;进口流速由实测值给定，紊动动能及紊动动能耗散率由k=0.003 75，ε =0.09k3/2给出［6］，Uin为进口断面平均流速，取0.85 m/s;出口断面利用充分发展条件;自由水面根据实测水位通过插值计算节点处的水位.

3 计算区域及网格剖分

采用上述模型对黄河宁夏沙坡头河段连续弯道的三维水流进行编程模拟计算，计算河段长约10 km，平均河宽为230.65 m，计算流量为 739.37 m3/s，上游水位 1 240.85 m，下游水位为1 240.65 m.计算区域如图1所示，共布设15个计算断面.研究区域采用结构网格进行剖分，划分为124×31×15个网格，共计57 660个节点，时间步长取为12 s.

4 实测和计算结果对比分析

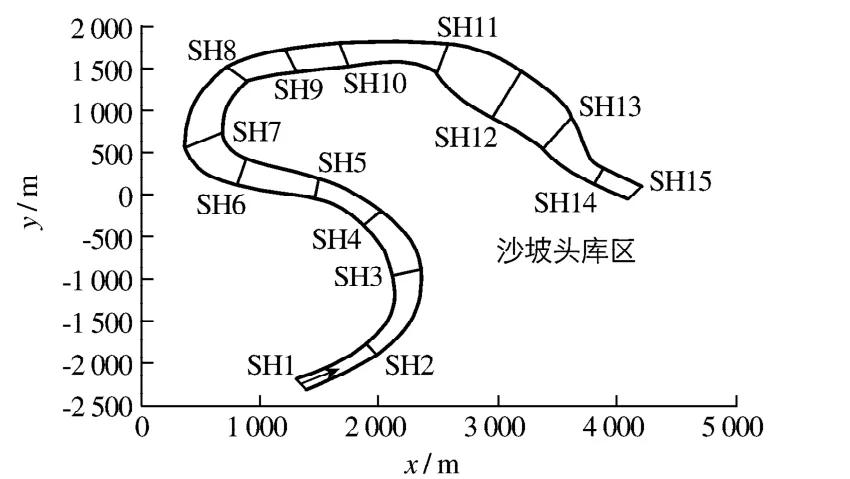
图1 河道示意图Fig.1 Sketch of river bends

4.1 沙坡头河段实测数据

为了检验数值模型和确定初始条件，2009年7月，项目组成员利用声学多普勒流速剖面仪、回声测深仪等先进设备赴黄河宁夏沙坡头河段对其中12个典型断面的河床高程、三维流速、河宽和水位等进行了实测.表2给出了典型断面的部分实测数据.

从实测数据中可以看出，水位从上游到下游呈下降趋势，断面SH1较窄，水流湍急;断面SH7较宽，水流相对较缓.

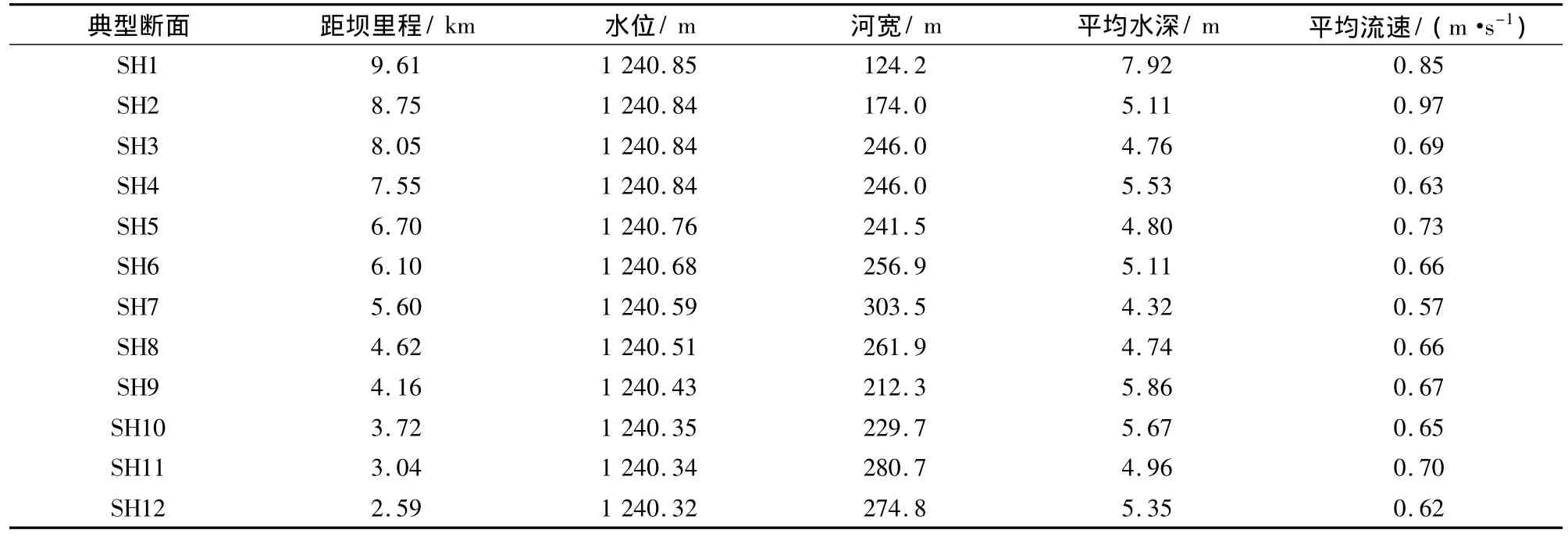
表2 典型断面部分实测数据Tab.2 Experimental data of typical sections

4.2 平面流场分布

本文采用MATLAB语言编写程序，对黄河宁夏沙坡头河段天然连续弯道进行了模拟计算.

图2给出了计算流速场的分布，从计算结果来看，在连续弯道中，一个弯顶处的平面流速分布和下一弯顶处的流速分布呈横向对称，且在两弯顶之间开始过渡.下一弯道入口尚残存有上一弯道未完全衰减的剩余环流，它将表层的高速水流移向凸岸，随着下一弯道中心角的增大，反向环流的影响沿程衰减，使纵向流速逐渐过渡到均匀分布，并使反向弯道环流得到充分发展.图3给出了两弯顶附近处纵向垂线平均流速沿河宽的分布，可以看出，模型计算值和实测值吻合较好.

图2 计算流场及平面流场Fig.2 Calculation velocity field and surface velocity field

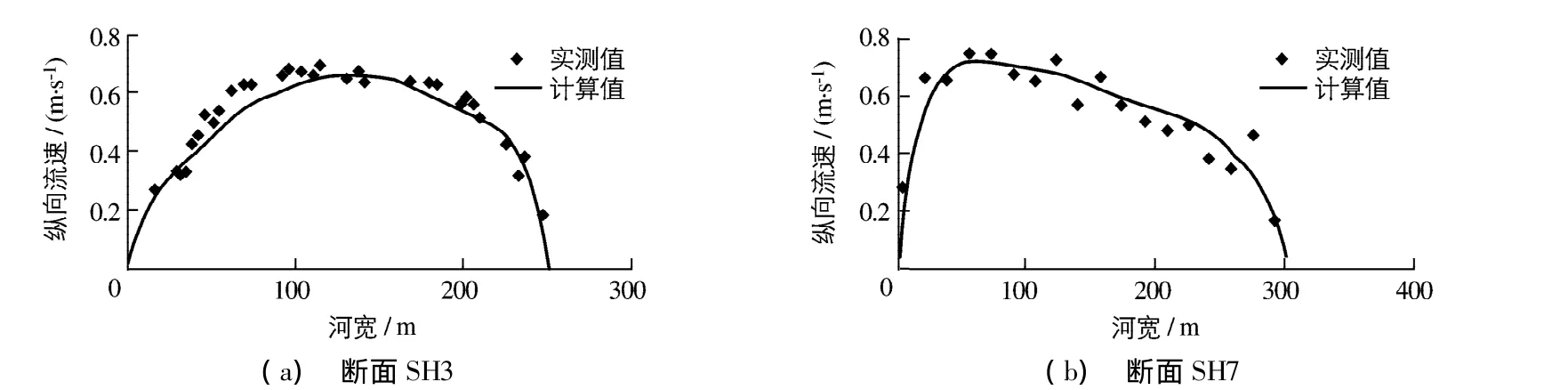
图3 计算流速和实测流速比较Fig.3 Comparison between simulated and measured velocity distributions

4.3 纵向流速沿垂线的分布

对连续弯道中典型断面的主流流速的计算值和实测值进行对比分析，断面SH1～SH5为第1个弯道，断面SH6～SH9为第2个弯道，y表示距左岸的距离.

图4 典型断面纵向流速的垂线分布Fig.4 Vertical distribution of longitudinal velocities of the typical sections

图4((a)～(h))为弯道断面上5条垂线处的纵向流速分布，可以看出，模型计算结果与实测结果较为接近，均体现了水流在连续弯道中的分布规律.水流进入第一个弯道后，主流开始逐渐向凹岸转移，且在弯道以下相当长的距离内，主流紧贴凹岸(图4(a)～(d));当水流进入下一个弯道时，开始过渡，过渡段的流速分布比较均匀(图4(e)～(f));越过弯顶后，又逐渐偏向凹岸(图4(g)～(h)).

4.4 横向流速分布

在弯道中，由于惯性离心力的存在，水流沿轴向运动的同时，所有的水质点又受到同样的径向压力梯度，使得近水面的水质点向凹岸运动，而近底的水质点向凸岸运动(见图5).由图5可见，水流进入第一个弯段后，最大横向环流强度出现在弯顶后半段(断面SH4～SH5).中间过渡段(SH6)既是反向弯道的过渡段也是环流转化方向的过渡段，此处环流方向已经转为反向，只是环流强度比较弱.下一弯道中环流的发展由于受到上一弯道的抑制作用，环流在弯顶后半部分出现且较明显，断面(SH8～SH10)横向环流发展并出现加速的过程.总体上来看，本模型的计算结果是合理的，平面流速、断面纵向垂线流速和二次流都较好地反映了实际流场的分布.

图5 断面横向流速矢量场Fig.5 Transverse velocity distribution of sections

5 结语

本文对笛卡尔坐标系下的Reynolds应力方程进行了三维适体坐标变换，建立了天然连续弯道河流的修正k－ε湍流模型.针对天然弯曲河流，由于环流和水面比降的影响，水面沿程变化较大.首先通过实测水位插值得到计算节点上的水位，用这一水位作为计算区域的表面，采用“刚盖”假定近似自由水面.利用有限体积法离散控制方程，基于SIMPLEC算法编程求解，并利用黄河宁夏沙坡头河段的实测资料进行了验证.结果表明:模型计算的流速分布与实测资料吻合较好，说明该模型可以模拟天然河流的三维水流特性，为下一步研究该河段的泥沙冲淤和河床演变情况奠定了基础.计算结果还表明，自然界中河弯多以非对称形式出现，非对称河弯在两弯顶中间存在较多低流速区，在这些区域将会形成泥沙淤落，另外对岸流速一般较大，从而推动弯道整体以较快的速度向下游迁徙.

［1］宋志尧.罗索夫斯基弯道环流公式的统一［J］.水科学进展，2003，14(2):218-221.(SONG Zhi-yao.Generality of the Rozovskii's formulas on circulation at river bends［J］.Advances in Water Science，2003，14(2):218-221.(in Chinese))

［2］许栋，刘召平，乾爱国，等.弯曲河道中水流运动的三维数值模拟［J］.水利学报，2010，41(12):1423-1431.(XU Dong，LIU Zhao-ping，QIAN Ai-guo，et al.Three-dimensional numerical simulation of flow in river bends［J］.Journal of Hydraulic Engineering，2010，41(12):1423-1431.(in Chinese))

［3］ZHANG Xiao-feng，CUI Zhan-feng，LU Xin-hua.Simulation of sediment deposition in a cavity with free surface［J］.Journal of Hydrodynamics，2010，22(50):626-633.

［4］姚仕明，王兴奎，张超，等.曲线同位网格的三维水流数学模型［J］.清华大学学报:自然科学版，2006，46(3):336-340.(YAO Shi-ming，WANG Xing-kui，ZHANG Chao，et al.3-D numerical flow model in curvilinear coordinates with collocated grid［J］.Journal of Tsinghua University(Science and Technology)，2006，46(3):336-340.(in Chinese))

［5］SHEN Yong-ming，LIU Cheng.A three-dimensional k-ε-kp model in curvilinear coordinates for sediment movement and bed evolution［J］.Sci China Ser E-Tech Sci，2009，52(4):1090-1100.

［6］陈青毅，吴卫，刘桦.河口水库库内三维流动数值模拟［J］.水动力学研究与进展:A辑，2011，26(2):140-149.(CHEN Qing-yi，WU Wei，LIU Hua.Numerical simulation of three dimensional flows in estuarine reservoir［J］.Chinese Journal of Hydrodynamics，2011，26(2):140-149.(in Chinese))

［7］易雨君，王兆印，张尚弘.考虑弯道环流影响的平面二维水沙数学模型［J］.水力发电学报，2010，29(1):126-136.(YI Yu-jun，WANG Zhao-yin，ZHANG Shang-hong.Two-dimensional sedimentation model of channel bend(Part 2)-Verification and application［J］.Journal of Hydroelectric Engineering，2010，29(1):126-136.(in Chinese))

［8］吴修广，沈永明，潘存鸿.天然弯曲河流的三维数值模拟［J］.力学学报，2005，37(6):679-696.(WU Xiu-guang，SHEN Yong-ming，PAN Cun-hong.Three dimensional numerical simulation of natural curved river［J］.Acta Mechanica Sinica，2005，37(6):679-696.(in Chinese))

［9］李琳琳，余锡平.裁弯对上下游流态影响的三维数学模型研究［J］.水力发电学报，2010，29(5):183-189.(LI Lin-lin，YU Xi-ping.Study on effects of river cutoffs by a 3-D numerical model［J］.Journal of Hydroelectric Engineering，2010，29(5):183-189.(in Chinese))

［10］ABHARI M N，GHODSIAN M，VAGHEFI M，et al.Experimental and numerical simulation of flow in a 90°bend［J］.Flow Measurement and Instrumentation，2010，21:292-298.

［11］SHIH T H，LIOU W W，SHABBIR A，et al.A new k－ε eddy viscosity model for high Reynolds number turbulent flows［J］.Computers and Fluids，1995，24(3):227-238.

［12］ZHANG Jian-min，CHEN Jian-gang，XU Wei-lin，et al.Three-dimensional numerical simulation of aerated flows downstream sudden fall aerator expansion-in a tunnel［J］.Journal of Hydrodynamics，2011，23(1):71-80.

［13］YE Fei，GAO Xue-ping.Numerical simulations of the hydraulic characteristics of side inlet/outlets［J］.Journal of Hydrodynamics，2011，23(1):48-54.

［14］陶文铨.数值传热学［M］.西安:西安交通大学出版社，1995.(TAO Wen-quan.Numerical heat transfer［M］.Xi'an:Xi'an Jiaotong University Press，1995.(in Chinese))

［15］景何仿，李春光，吕岁菊，等.黄河沙坡头连续弯道水流运动三维数值模拟［J］.宁夏大学学报:自然科学版，2010，31(3):198-202.(JING He-fang，LI Chun-guang，LV Sui-ju，et al.Three-dimensional numerical simulation of the Yellow River flow in Shapotou consective curves［J］.Journal of Ningxia University(Natural Science Edition)，2010，31(3):198-202.(in Chinese))