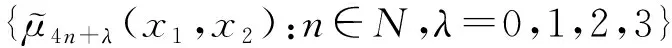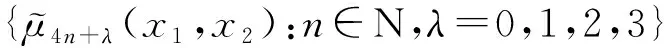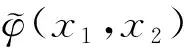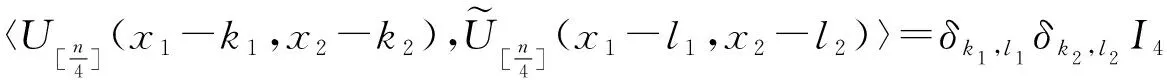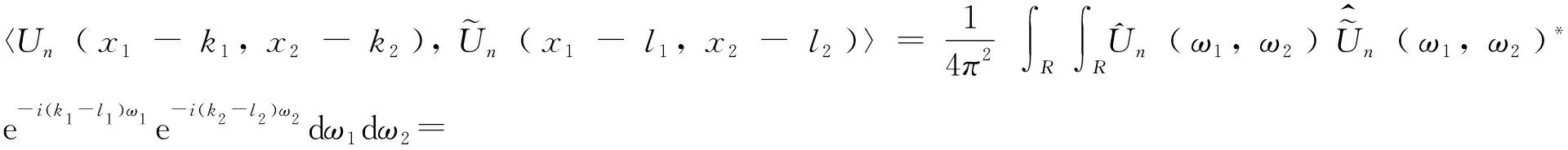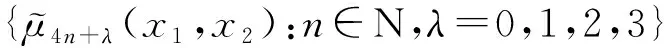二维四向双正交小波包
库福立,王刚,王亚玲
(新疆师范大学数学科学学院,新疆 乌鲁木齐,830054)
0 引言
小波分析是近年来发展起来的一门新兴数学分支,它是Fourier分析划时代发展的结果,在信号分析、图像处理、模式识别、语言合成、方程求解和分形力学等领域都取得了具有科学意义和应用价值的重要成果.然而L2(R)中函数生成的正交小波包具有很差的频域局部化,小波包的这些优良性质在图像压缩、编码理论等方面得到广泛应用.于是由Coifman和Meyer在文献[1-2]中引入一元正交小波包的概念,目的是进一步分解小波;而崔锦泰和李淳把正交小波包推广到非正交小波包;Daubechies和Cohen在文献[3]中引入双正交小波包的概念;冷劲松和程正兴[4]给出多尺度多重双正交小波包;陈清江和程正兴[5-6]给出了高维向量值双正交小波包.然而,在现代科技中,高维的小波应用十分广泛,相应的高维小波研究也尤其重要.杨守志教授在文献[7]中给出双向小波函数和尺度函数的概念,本文中推广一元双正交双向小波包的概念,给出双向双正交小波包的定义及其构造;讨论二元双向双正交小波包的性质,并得到相关结论.
1 预备知识
为了方便,我们引入记号:∀f(x1,x2),g(x1,x2)∈L2(R2),内积定义如下:
(1)

(2)
定义张量积设F和G是两个一元函数空间.F的基底是{fk(x)}j∈Z,G的基底是{gk(y)}j∈Z,把以{fk(x)gk(y)}k∈Z为基底的二元函数空间H称为空间F和G的张量积空间,并表示为:
H=F⊗G
(3)
对于二元函数我们有:
φ(x,y)=φ(x)φ(y)
(4)
2 二维四向多分辨分析
定义2.1设φ(x1,x2)∈L2(R2),我们定义子空间序列{Vj}j∈Z⊂L2(R2):
Vj=ClosL2(R2)〈2jφ(2jx1-k1,2jx2-k2),2jφ(2jx1-k1,k2-2jx2),2jφ(k1-2jx1,2jx2-k2),2jφ(k1-2jx1,k2-2jx2):k1,k2∈Z〉
(5)
生成L2(R2)中的一个多分辨分析(MRA){Vj}j∈Z,当且仅当(5)式定义的{Vj}j∈Z满足:
(ⅰ)…⊂V-1⊂V0⊂V1⊂…;


(ⅳ)f(x1,x2)∈Vj⟺f(2x1,2x2)∈Vj+1;
(ⅴ)存在L2(R2)中的一个函数φ(x1,x2),使集合{φ(x1-k1,x2-k2),φ(x1-k1,k2-x2),φ(k1-x1,x2-k2),φ(k1-x1,k2-x2):k1,k2∈Z}是V0的Riesz基.于是,我们可得找到两个常数0 (6) 定义2.2由文献[7]中给出双向单小波的定义,现在利用两个一元双向单小波φ(x)和φ(y)通过它们的张量积构造二维空间上的二维四向双向小波.设双向细分函数φ(x)和φ(y)分别满足细分方程: (7) (8) 令φ(x,y)=φ(x)φ(y),则可以得到: (9) (10) (11) (12) 对(10)和(11)式变形得: (13) (14) (15) 分别对(13~15)作Fourier变换得: (16) (17) (18) 令: φ(x1,x2)=[φ(x1,x2),φ(x1,-x2),φ(-x1,x2),φ(-x1,-x2)]T (19) (20) 于是我们得到式(19)和式(20)的加细面具符号: (21) (22) 定义3.1若二维四向尺度函数φ(x1,x2)是正交的,则满足下列式子: 〈φ(x1,x2),φ(x1-k1,x2-k2)〉=δ0,k1δ0,k2;〈φ(x1,x2),φ(k1-x1,x2-k2)〉=0;〈φ(x1,x2),φ(x1-k1,k2-x2)〉=0;〈φ(x1,x2),φ(k1-x1,k2-x2)〉=0. (23) (24) (25) (26) (27) 于是我们得到(26)、(27)的Fourier变换: (28) (29) (30) (31) (32) (33) 引入记号: (34) (35) 对应的Fourier形式为: (36) 令 U4n+λ(x1,x2)=[μ4n+λ(x1,x2),μ4n+λ(x1,-x2),μ4n+λ(-x1,x2),μ4n+λ(-x1,-x2)]T (37) 于是,我们可以得到: (38) 的加细面具符号为: (39) 其中λ=0,1,2,3于是我们可以得到: (40) 引理5.1对∀n∈Z+进行4进制展开: (41) 上式总是一个有限和,并且展开式是唯一的. 引理5.1的证明若4S0-1≤n≤4S0,则有带余除法,我们有n=4S0+n1,我们再把n1展开,不断重复着这个过程,我们得到: n=εS04S0+εS14S1+εS24S2+…+εSk4Sk 其中,0 (42) 定理5.1的证明①当n=0,(43)式成立; 于是,我们得到: 于是有: 综合得,命题得证. (43) 定理5.3的证明要证明上式,只需证明下式成立: 该式证明由(32)式类似定理5.1证明,即得. [1] Daubechies I. Ten lectures on wavelets[M]. Philadephia: Society for Industrial and Applied Math,1992:227-249. [2] Coifman R R, Meyer Y, Wickerhauser M V. Their application[M]. Baston Jones and Bartlett MA,1992:145-150. [3] Cohen A, Daubenchies I. On the instability of arbitary biorthogonal wavelet packet[J]. SIAM J Math Anal,1993,24(5):1340-1354. [4] 冷劲松,程正兴,黄延祝:a尺度多重双正交小波包[J].工程数学学报,2001,18(小波专刊):124-130. [5] 陈清江,程正兴,冯晓霞.高维多重双正交小波包[J].应用数学,2005,18(3):358-364. [6] 陈清江,程正兴,杨守志.向量值正交小波包[J].应用数学,2005,18(4):505-515. [7] 杨守志,李尤发.具有高逼近阶和正则性的双向加细函数和双向小波[J].中国科学A辑,数学2007,37(7):770-795. [8] Chui C K, Wang J Z. On compactly supported spline wavelets and aduality principle[J]. Trans Amer Math Soc,1992,330:903-916. [9] Mallat S A. Theory for multi-resolution signal decomposition: the wavelet representation[J]. IEEE Trans on PAMI,1989,11(7):674-683. [10] Yang Shouzhi, Huang Yingdong. Construction of a class of compactly supported symmetric and balanced refinable function vector by GTST[J]. Appl Math and Computation,2009,207(1):83-89. [11] Yang Shouzhi, Xue Yanmei. Two-direction poly-scale refinability[J]. Computers and Mathematics with Application,2009,58(1):119-127. [12] 杨守志,彭立中.基于PTST方法构造高阶平衡的正交多尺度函数[J].中国科学:E辑,2006,36(6):644-656. [13] Yang Shouzhi. Extension of multi-reslution analysis and the construction of orthogonal multiwavelets[J]. Geogian Mathematical Journal,2005,12(3):561-571. [14] Shen Z. Nontensor product wavelet packets inL2(R2)[J]. Math Anal,1995,24(3):1061-1074. [15] Chui C K, Lian J. A study on orthonormal multi-wavelet[J]. J Appl Numer Math,1996(20):273-298. [16] Grossman A, Morlet J. Decomposition of Hardy Function into Square Integrable Wavelets of Constant Shape[J]. SLAM J Math,1984,18(15):723-736. [17] 杨守志,杨晓忠.广义基插值的正交多尺度函数和多小波[J].数学物理学报,2007,27A(3):470-475.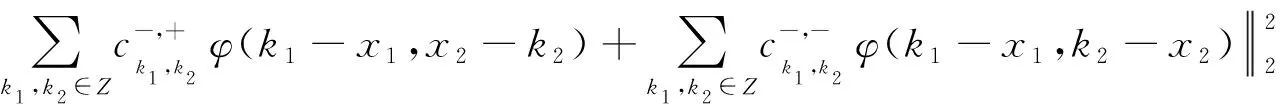



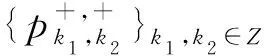

3 双正交的二维双向尺度函数和小波函数
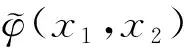
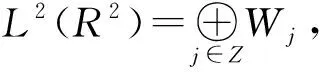
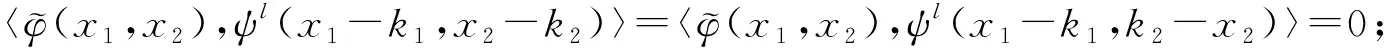

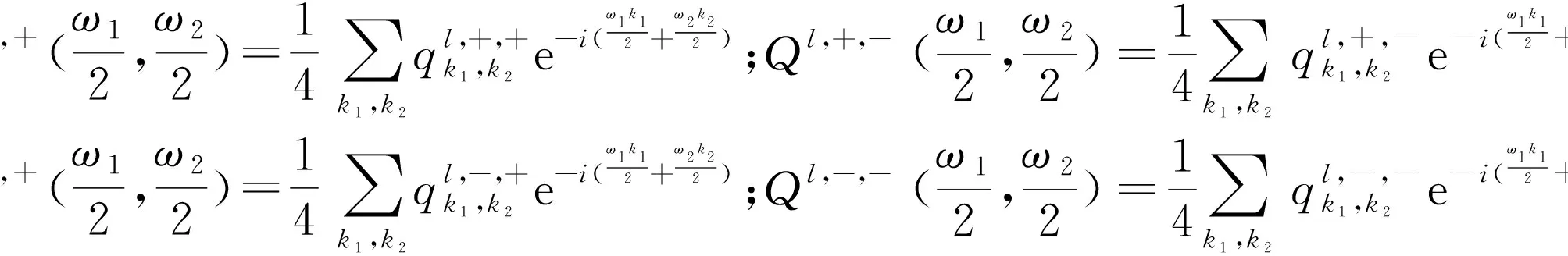
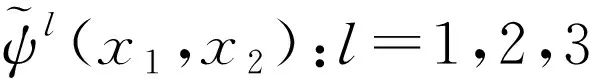

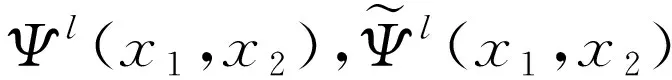
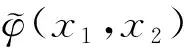
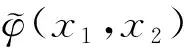
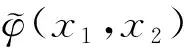
4 二维四向双正交小波包
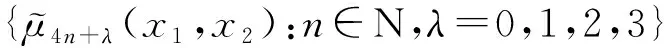
5 二维四向双正交小波的性质