以建筑物抗震设计为依据的爆破振动安全判别研究

杜耀志，刘 旺

(国防科技大学指挥军官基础教育学院， 湖南长沙 410072)

0 引言

目前，爆破振动安全判别通常以地面质点振动速度为主，辅以主振频率作为标准，速度－频率标准仅仅是对独立阈值理论的延伸，没有考虑到振动持续时间和结构动力特性的影响。近几年来，有人根据材料的动态拉应力破坏准则，利用质点振速与动态抗拉应力的关系，建立了一种新的判据，即动态抗拉应力判据，但由于建筑结构的动力特性和材料性能无法确定，使得这种判据指标对于不同场区和不同类型建筑结构的适应性较差，不具备推广应用价值。

鉴于爆破振动效应和地震效应对建构筑物的作用机理相同，以被保护对象(即目标建筑物)抗震设计为依据，探讨新的爆破振动安全判别途径和方法已经十分迫切和必要。

1 以抗震设计为依据判别爆破振动安全的科学性

1.1 完善现行爆破振动安全判别标准的必要性

爆破振动安全判别的对象往往是某一具体的建筑物，而结构类型相同的建筑物即使具有相同的自振频率，但因其建筑结构、场地、建筑材料的不同，使得它们对爆破振动效应的响应表现出巨大的差异。现行的爆破振动安全判别标准对不同建筑物以大类划分，对大类采用统一的判别标准，无法反映个体差异，因此，补充和完善现行的爆破振动安全判别标准，增强其针对性显得十分必要。

1.2 爆破振动与天然地震对建筑物的激励及破坏机理基本相同

爆破地震波和天然地震波都包括在介质内部传播的体波和沿地层表面传播的面波，其中面波的作用是导致建筑物破坏的主要原因。爆破振动与天然地震对建筑物的力学效应都表现为直接作用在结构体上的压力、拉力或剪切力，所以将力学响应特性作为爆破振动或天然地震对建筑物破坏与否的衡量指标，具有较强的合理性和可比性。

1.3 建筑物第一水准烈度的动态响应与爆破振动安全指标相对应

虽然建筑抗震设计是针对天然地震而言的，但由于爆破振动与地震之间具有相同的物理特性，所以抗震设计中对建筑物遭破坏作用的标准同样适用于爆破振动对建筑物的破坏作用。

地震基本烈度的确定反映了地震烈度衰减规律和震中距等影响的概率因素，它确定的是基本烈度在地域上的分布(见图1)。但是对于某一个地区，并不是每次地震都是按基本烈度发生的，也存在一个概率分布的问题。一般认为地震烈度的概率分布符合正态分布，其分布函数为:

式中:δ—烈度上限;

I—烈度;

ε—众值烈度(亦称为多遇地震烈度);

k—形状系数。

《建筑抗震设计规范》(GB50011―2010，以下简称《规范》)指出，在建筑物遭遇第一水准烈度(众值烈度)时，结构处于正常使用状态，从结构抗震分析角度，可视为弹性体系，采用弹性反应谱进行弹性分析［1］。因此，爆破振动对建筑物构成的影响程度必须控制在弹性范围内，即在爆破振动的作用下，建筑物一直处于弹性工作阶段，不能出现非弹性变形［2］，在安全判别时必须以建筑物设计遭遇第一水准烈度为判据阈值，也就是说爆破振动作用下建筑物受到的最大剪切力Qmax要小于建筑物在遭遇第一水准烈度时的最大剪切力阈值，即《规范》中的水平地震作用标准值FEK。

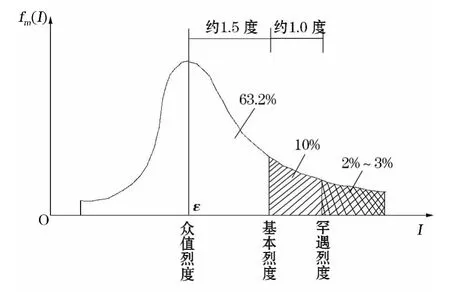
图1 地震烈度的概率分布

2 以抗震设计为依据的爆破振动安全判别方法

2.1 水平地震作用标准值的计算

2.1.1 确定水平地震影响系数最大值

《规范》把抗震等级分为4级，其中第1级代表最高的抗震设计要求，第4级代表最低的要求。建筑物抗震设计应根据烈度、结构类型以及房屋的高度按《规范》确定结构的抗震等级。对于爆破振动安全标准而言，依据具体建筑物的结构类型和所设计的抗震等级便可根据《规范》反推出其可抗地震烈度。

地震烈度是指某一地区、地面即房屋建筑等工程结构遭受到一次地震影响的强烈程度。我国根据房屋建筑震害指数、地表破坏程度即地面运动加速度指标将地震烈度分为12度，制定了《中国地震烈度表》。

《规范》中列出了不同地震烈度分别在多遇地震和罕遇地震下所对应的水平地震影响系数最大值(见表1)。

表1 水平地震影响系数最大值αmax

2.1.2 确定场地的特征周期值

场地的特征周期是根据场地类别和抗震设计分组得出的，见表2。

2.1.3 确定地震影响系数

《规范》给出了地震影响系数α与结构自振周期T的关系曲线及计算公式(见图2)。

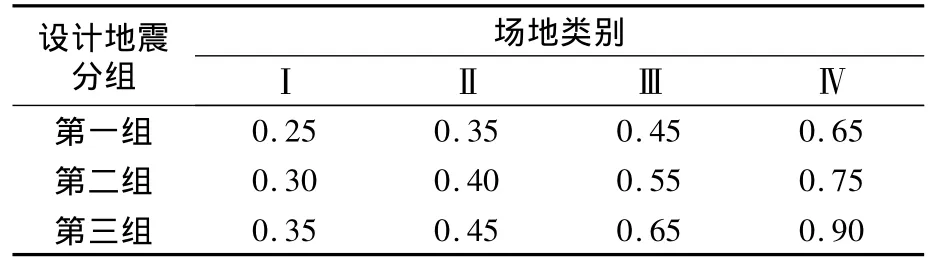
表2 特征周期值Tg(S)

图2 α与结构自振周期T的关系曲线

其中:αmax—水平地震影响系数最大值;

Tg—特征周期值;

T—结构自振周期;

ξ—结构的阻尼比;

η1—斜率调整系数;

η2—阻尼调整系数

2.1.4 计算水平地震作用标准值

我国在建筑物抗震验算中，采用二阶段设计，实现三水准设防目标。其中的第一阶段设计为承载力验算，同理，爆破振动对建筑物的影响应该控制在该阶段之内。该阶段是取第一水准的地震参数来计算结构的弹性地震作用标准值和相应的地震作用效应［3］。

式中:FEK—水平地震作用标准值;

α—地震影响系数;

β—动力系数;

G—重力荷载代表值，G=mg，m为建筑物的自重，g为重力加速度。

FEK即目标建筑物在弹性反应阶段最大允许剪切作用力，换言之，爆破振动对目标建筑物的剪切作用力不得大于FEK。

2.2 爆破振动对目标建筑物的动态响应和最大剪切力计算

在单质点弹性体系的水平地震反应理论中，根据达朗伯原理，质点在运动的任一瞬时，作用在质点上的阻尼力)，弹性恢复力 Kx(t)和惯性力处于瞬时平衡状态，即:

其中:c—阻尼系数(或粘滞阻尼);

x(t)—质点对地面的相对位移;

K—抗侧移刚度或称之为弹簧常数。

一般称ω为体系的自振频率(也称角频率)。对应于给定的固有周期和阻尼比，把最大位移xmax乘以弹簧常数K，即可得到最大剪切力:

根据以上步骤所得参数，以实测爆破振动地面加速度为输入，便可得出在爆破振动作用下的目标建筑物受力时程曲线。

2.3 爆破振动安全判别标准

爆破振动作用下判定目标建筑物是否安全的判别式为:Qmax＜FEK，即Qmax＜FEK则判定爆破振动作用对目标建筑物是安全的，否则反之。

3 工程实例与分析

在浏阳河大桥拆除爆破中，以待爆桥附近的一处三层框架结构民用建筑为爆破振动监测点。根据实测数据，利用以上安全标准对该建筑物进行爆破振动安全判别。抗震设计参数见表3。

表3 抗震设计参数

根据该建筑物抗震设计执行标准及设计参数有:

Tg=0.35 s，αmax=0.16 ，ξ=0.05 ，T=0.65s，m=127400 kg

由于所用测振仪为速度型，应利用测振分析软件对所测数据进行微分得到加速度时程数据。依据单质点振动反应谱理论进行matlab编程，分析相对位移反应波形、相对速度反应波形和绝对加速度反应波形［4］，得出最大相对位移 xmax=0.0029 cm，最大相对速度 vmax=0.0284 cm/s，最大绝对加速度amax=1.2819 cm/s2。

则:Qmax＜FEK

依此判断，此次浏阳河大桥爆破拆除的爆破振动作用不会对目标建筑物造成破坏。爆破后，对目标建筑物进行了全面检测，结果表明，上述判断与实际结果相符。

4 结论

以建筑物抗震设计为依据，充分考虑建筑物自身特性和场地特性受爆破振动效应的影响因素，针对具体的建筑物相对应地给出爆破振动的安全判据值，从而保证对爆破振动的安全判别具有较强的针对性和科学性。本文只仅仅进行了一些初步探讨，实验验证的样本数还远远不够，是否具有实用价值有待进一步深入研究。

［1］GB50011—2010.建筑抗震设计规范［S］.

［2］丁建国.弹塑性反应谱及其在抗震设计中的应用［J］.南京理工大学学报，2007，31(6):780-783.

［3］尚守平.结构抗震设计［M］.北京:高等教育出版社，2003:40-46.

［4］［日］大崎顺彦，田琪译.地震动的谱分析入门(第二版)［M］.北京:地震出版社，2008:132-145.