阈值阵列模型下的超阈值随机共振信噪比增益

张礁石 杨子贤 卢结成

（中国科学技术大学信息科学技术学院，合肥，230027）

引 言

随机共振（Stochastic resonance，SR）是一种现象：在某些非线性系统中，衡量随机共振的测度（如输出信噪比增益、互信息量等）随着加入噪声的改变呈现出非单调变化的规律。国内外早期的研究大多集中在一类非线性动态系统——双稳态系统［1］其中V（x）＝但该模型受限于绝热近似理论（A≪1，Ω≪1）。

Wiesenfeld［2］等在1994年首次提出SR实际上是一种阈值效应，低阈值信号、噪声、阈值系统是产生SR现象的必需因素。在2000年Stocks［3］提出超阈值SR概念以前，人们仅研究由一个阈值单元组成的SR系统，并认为只有当输入信号幅值低于系统阈值时（即输入为低阈值信号），才能产生SR现象。Stocks提出阈值阵列模型，证实当输入信号幅值高于系统阈值时 （即输入为超阈值信号），通过此模型可得到另一种形式的SR现象——超阈值SR（Suprathreshold SR）。目前，对于超阈值SR的研究主要针对非周期信号输入信号下，输入输出互信息量［3］、输入输出相关系数［4］等随阈值噪声的加入非单调变化的情况，但对于周期输入却很少有研究。

对于周期输入，采用输出信噪比增益来衡量其SR测度。本文采用阈值阵列模型为研究对象，研究输出信噪比增益是否大于1的问题。然而，与之前对于输出信噪比增益研究不同的是，本文所处理的输入信号为周期信号与噪声的混合信号，即含噪信号。这样一来，输入信噪比是固定的，通过阈值阵列系统，在阈值噪声的作用下 （注意，含噪输入信号通过阈值阵列系统又受到阈值噪声的作用，相当于在本来就受污染的信号中再加入噪声），可观察到输出信噪比相对于输入信噪比有所提高（即输出信噪比增益大于1），且输出信噪比增益随着阈值噪声方差的变化而非单调变化。从黑盒角度看，对原本含噪声的信号进行处理，期望其输出信噪比相比输入信噪比增加，相当于对输入信号进行滤波去噪。而阈值阵列系统就等价于这个滤波器。只不过这个特殊的非线性滤波器借助了噪声的有效性，对“模糊”的输入信号进行处理，得到更“清晰”的输出信号。

1 随机共振的测度——信噪比增益

最早用于衡量SR现象是否存在的标志就是信噪比是否得到改善，人们对于SR是否能够使系统输出信噪比高于输入信噪比存在争论［4］。但公认的是，在线性响应理论下，限定输入信号幅值远小于噪声幅值，SR不能提供大于1的信噪比增益。本文利用超阈值SR理论模型证实在周期输入信号下可获得大于1的信噪比增益。

Chapeau［5］提出的静态阈值SR理论中给出输出信噪比为输出信号谐频m／Ts上的谱线高度与附近带宽ΔB内噪声功率之比

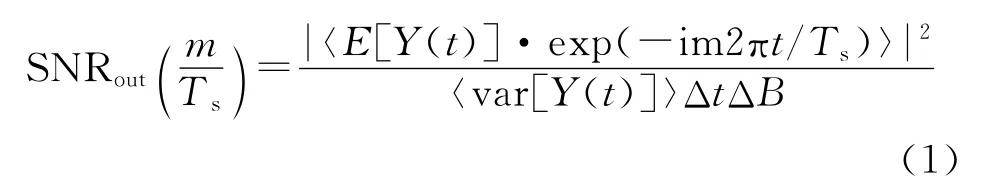
式中：〈·〉代表时域平均，E［Y（t）］为输出信号均值，var［Y（t）］为输出信号方差。

输入信噪比为

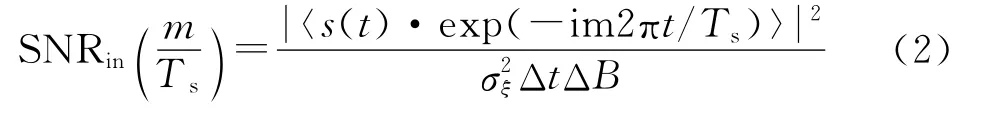
式中：s（t）为输入有用信号为输入噪声ξ（t）的方差。

输出信噪比增益为

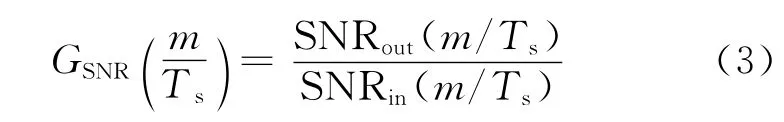
式中：m／Ts表示输出信号谐频，文中仅研究m＝1的情况，即输出信号基频。

2 阈值阵列模型

最初，人们研究的阈值SR是基于单阈值模型的，该模型的传递函数为

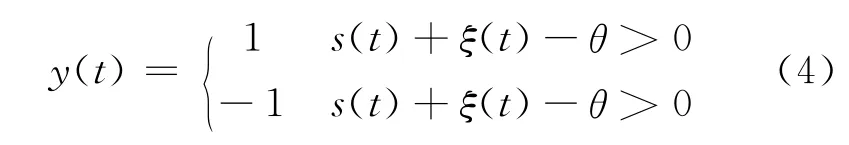
式中：s（t）为输入信号，ξ（t）为引入的噪声项，θ为系统阈值，y（t）为输出信号。对于超阈值周期信号输入，单阈值系统输出信噪比增益小于1。

文献［3］研究以非周期信号为输入的超阈值SR，提出了阈值阵列模型，如图1所示，该模型由N个独立的阈值单元组成，在N个阈值单元的输入端分别引入独立同分布的加性阈值噪声，将N个阈值单元的输出累加得到系统的输出。

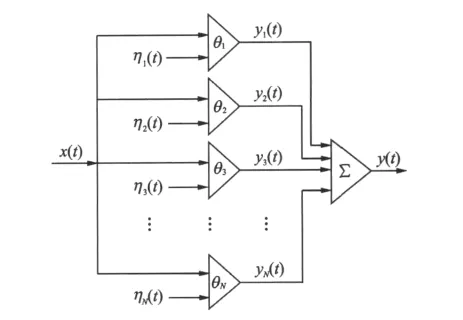
图1 非周期输入超阈值SR阈值阵列模型

此处引入集总平均（Ensemble averaging，EA）的概念［6］：最初由统计学中提出，后被引入到信息领域，EA技术曾广泛应用在声纳信号处理中，并在生物信号、雷达信号、神经元信号处理等中得到应用。

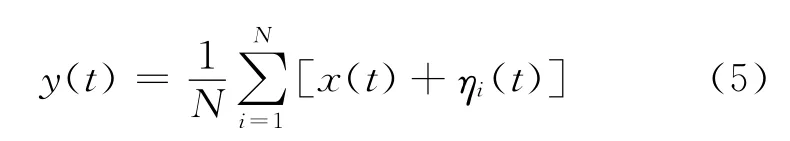
EA可由式（5）描述，输入周期信号x（t）与噪声的N次独立实现样本η1（t），η2（t），…，ηN（t）相加（N个独立同分布的噪声样本与输入周期信号叠加得到N个含噪信号样本），并对累加结果取平均，得到输出信号y（t）。若输入噪声η（t）的方差为σ2，那么输出信号y（t）的方差为σ2／N；则输出信号的信噪比SNR会提高约N倍。鉴于集总平均能改善周期信号的信噪比，可在单阈值系统之后级联集总平均器，改善单阈值系统的输出信噪比。本文提出适用于周期输入的超阈值SR系统，如图2所示。图2所示系统展开可得图3所示的周期输入下的超阈值SR阈值阵列模型。

图2 阈值系统与集总平均器的级联

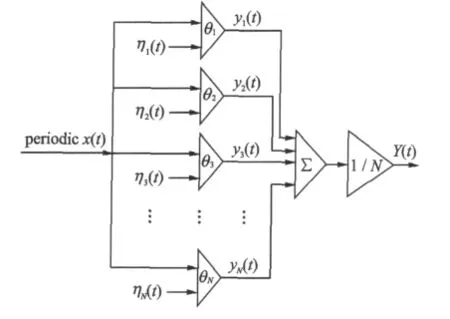
图3 周期输入的超阈值SR阈值阵列模型

基于超阈值SR的阈值阵列共有N个阈值单元，每个阈值单元有两个输入端。其中一个为共同输入x（t），另一个输入端引入阈值噪声ηi（t），N个阈值单元输入的阈值噪声彼此独立且同分布，其概率密度函数（Probability density function，PDF）为fη（η），分布函数（Cumulative distribution function，CDF）为Fη（η）。第i个阈值单元的阈值为θi，在阈值噪声ηi（t）的作用下，其输出为

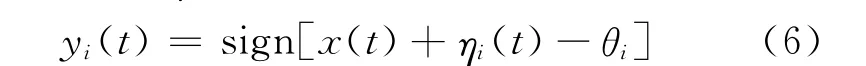
式中：sign为符号函数，

x

（

t

）＋

ηi

（

t

）－

θi

＞0，

yi

（

t

）＝1，或

yi

（

t

）＝－1。

N

个阈值单元的输出累加后平均得到系统输出，即

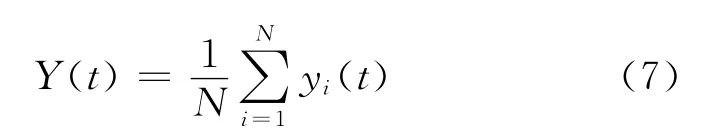
本文研究的输入为有用信号和噪声的混合，x（t）＝s（t）＋ξ（t），即s（t）为输入周期信号，ξ（t）为高斯白噪声，其PDF为fξ（ξ）。固定所有阈值单元的阈值为θi＝θ，i＝1，2，…N。则根据条件期望公式可知

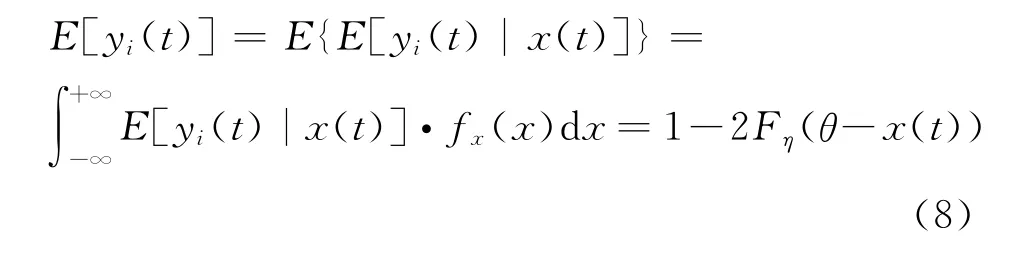
由x（t）＝s（t）＋ξ（t），则x（t）的 PDF 为fξ（x－s（t）），且E［yi（t）］，i＝1，2，…，N都相等，所以

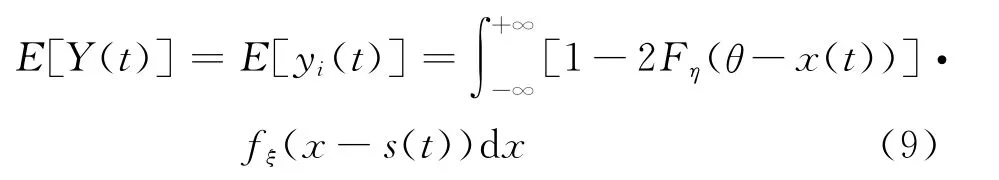
同理

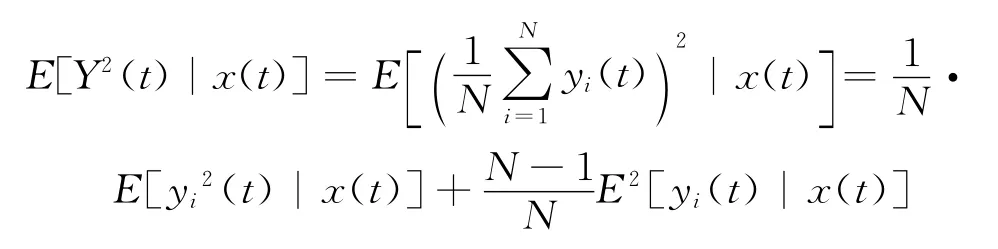
由式（6）知E［（t）｜x（t）］＝1，所以

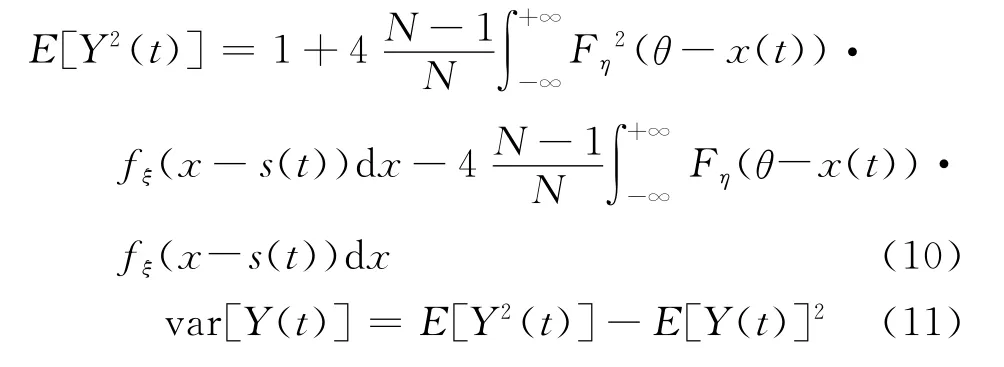
3 信噪比增益的实验分析

3.1 高斯输入噪声下的超阈值SR

考虑输入信号x（t）为余弦周期信号s（t）＝a·cos（2πt／Ts）与均值为0、方差为的独立高斯白噪声ξ（t）的混合，在阈值阵列中，每个单元的阈值噪声η1（t），…，ηN（t）为独立同分布的均值为0、方差为的高斯白噪声，且ηi（t）独立于x（t）。s（t）频率1／Ts＝0.1Hz，采样频率为1Hz，ξ（t）的方差＝0.5或1，固定所有单元的阈值为θi＝0。图4所示为输出信噪比增益GSNR随阈值噪声η（t）方差递增产生非单调的变化。因为输入信号x（t）已经确定，即输入信噪比SNRin是常数，所以图4也可以看作是输出信噪比SNRout随着阈值噪声η（t）加入产生的非单调变化。

图4中每条曲线代表不同的阈值单元个数，从1到1 024。当N＝1时，输出信噪比增益GSNR随阈值噪声η（t）的加入逐渐降低，这也是直观的感觉：加入噪声使得有用信号变得模糊。这也证明了在输入为超阈值信号时，单个阈值单元无法产生SR现象。此处“超阈值”并非指输入信号任何时候都大于阈值，而是指输入信号有时在阈值之上，有时在阈值之下。当阈值为输入信号均值时，阈值阵列系统的性能将达到最优［7］。这里选择的阈值θi＝0就是输入信号x（t）的均值。当N＞1，随着阈值噪声的加入，信噪比增益曲线会产生非单调的变化，且N越大，曲线峰值越高。但是当N很大（大于256）时，峰值趋于稳定。当s（t）的幅值为1，考虑输入噪声方差＝1和＝0.5两种情况，分布如图4（a，b）所示。图4（a）中“×”标记N＝1 024时GSNR的峰值为1.036 2，对应的阈值噪声方差为1.45。图4（b）中“×”标记N＝1 024时GSNR的峰值为 1.257 1，对应的 阈 值噪声 方差为 0.60。GSNR＞1被认为是阈值阵列系统对输入含噪信号产生积极作用的标志。图4（a）中随着N的继续增加，GSNR趋于恒定，仅在1附近。图4（b）中当N＝8时，GSNR开始超越1，峰值在1.2附近。

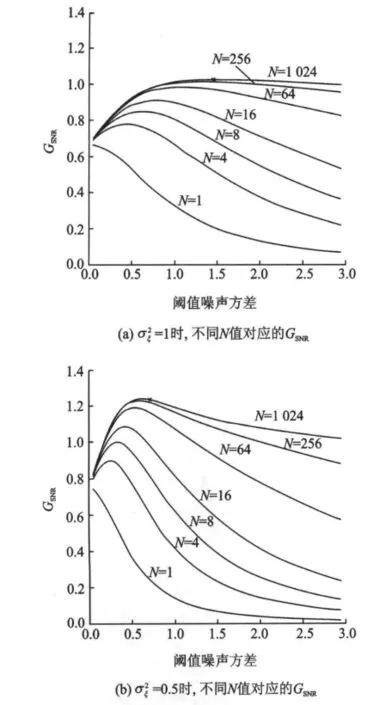
图4 对于不同的阈值单元个数N，GSNR随阈值噪声方差增加非单调地变化

值得一提的是，超阈值SR不再适合强噪声下的微弱输入信号，而是要求输入噪声强度小于有用信号幅度或二者相当。图5所示的每条曲线对应不同的输入有用信号s（t）＝a·cos（2πt／Ts）幅值a，GSNR随阈值噪声η（t）方差的递增产生非单调的变化。其中阈值单元个数N为64，输入噪声ξ（t）的方差＝1。可知，当a＜1时，GSNR始终不能突破1，而当a＝1.2时，GSNR大于1，并随着a的增加而上升。

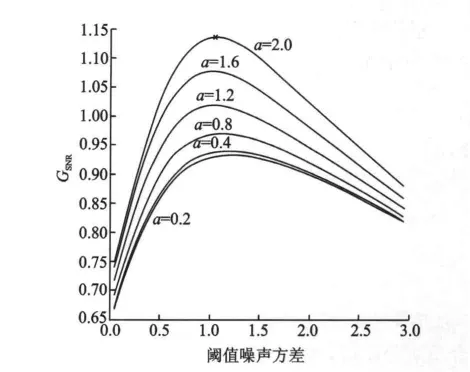
图5 对不同的s（t）幅值a，GSNR随阈值噪声方差的变化

3.2 非高斯输入噪声下的超阈值SR

以上实验都是限定输入噪声服从高斯分布的情况下进行的。文献［8］研究在非高斯噪声中利用阈值阵列SR系统检测微弱周期信号。典型的非高斯噪声服从拉普拉斯分布（Laplacian Gaussian）和混合高斯分布（Gaussian mixture）。服从拉普拉斯分布，均值为0，方差为的噪声其PDF为

当输入信号为余弦信号与拉普拉斯噪声的混合时，通过阈值阵列系统后，输出GSNR的变化如图6所示，其中，s（t）幅值a为1，ξ（t）均值为0，方差＝1。当输入噪声ξ（t）服从Laplacian分布时，输出信噪比增益GSNR随阈值噪声方差的增加非单调地变化。

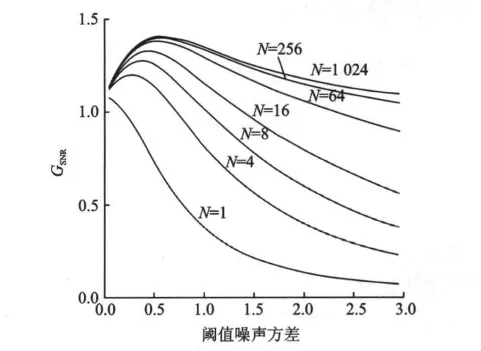
图6 输入噪声服从Laplacian分布时，GSNR随阈值噪声方差的变化

服从混合高斯分布，均值为0，方差为σξ2的噪声其PDF为

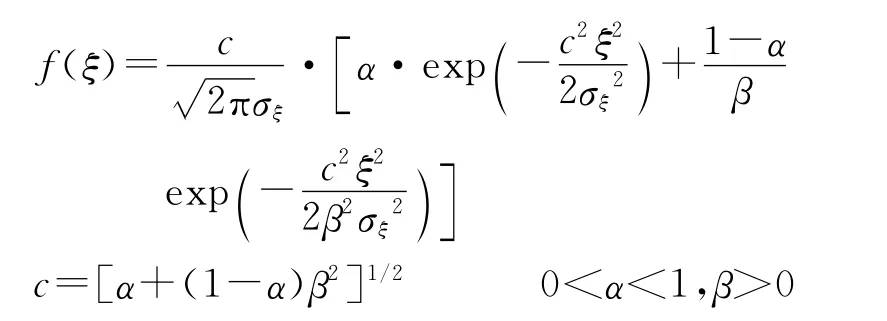
当输入噪声ξ（t）服从混合高斯分布时，α＝0.5，β＝0.5，其余条件同图6，输出信噪比增益GSNR的变化如图7所示。当输入噪声ξ（t）服从混合高斯分布时，输出信噪比增益GSNR随阈值噪声方差的增加非单调地变化。

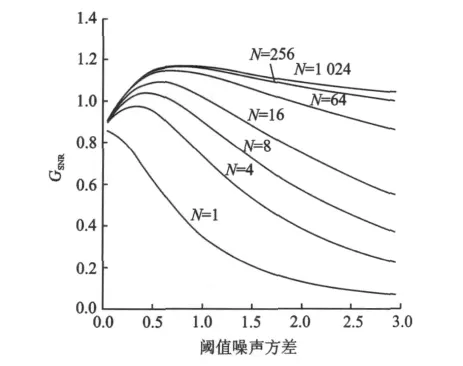
图7 输入噪声服从混合高斯分布时，GSNR随阈值噪声方差的变化

由图6，7可以看出，在相同条件下，当输入噪声服从非高斯分布，相比服从高斯分布情况，可以获得更好的输出信噪比增益。而且，非高斯情况下，当输入信号幅值不大于输入噪声的均方根时，也可以产生大于1的信噪比增益。可以认为GSNR＞1不仅与阈值阵列模型参数有关，也与输入噪声的分布及方差有关。

4 结束语

综上所述，本文研究了输入超阈值周期信号和不同分布的输入噪声混合，经阈值阵列系统得到了输出信噪比大于输入信噪比（即输出信噪比增益大于1）的结果，这正是超阈值SR现象的体现。尽管很多学者认为输出信噪比增益作为衡量SR的测度实践性较小。然而，在一般的信号处理中，总是先对输入信号进行滤波，尽可能滤除有害噪声，再将滤波后的信号送入信号处理单元，如果利用阈值阵列系统对输入信号进行预处理，利用噪声的有效性，提高其信噪比，则可能会获得更好的效果。目前在图像分割［9］和数字图像水印［10］检测领域，超阈值SR均得到应用。

［1］Gammaitoni L，Hanggi P，Jung P，et al.Stochastic resonance［J］.Reviews of Modern Physics，1998，70（1）：223－287.

［2］Wiesenfeld K，Pierson D.Stochastic resonance on a circle［J］.Physical Review Letters，1994，72（14）：2125－2129.

［3］Stocks N G.Suprathreshold stochastic resonance in multilevel threshold systems［J］.Physical Review Letters，2000，84（11）：2310－2313.

［4］McDonnell M D.Theoretical aspects of stochastic signal quantisation and suprathreshold stochastic resonance［D］.Australia：University of Adelaide，2006：102－130.

［5］Chapeau F，Godivier X.Theory of stochastic resonance in signal transmission by static nonlinear systems［J］.Physical Review E，1997，55（2）：1478－1495.

［6］Rompelman O，Ros H H.Coherent averaging technique：A tutorial review.Part 1：Noise reduction and the equivalent filter［J］.Journal of Biomedical Engineering，1986，8（1）：24－29.

［7］Stocks N G.Information transmission in parallel threshold arrays：Suprathreshold stochastic resonance［J］.Physical Review E，2001，63（4）：1－9.

［8］Rousseau D， Anand G V，Chapeau F. Noiseenhanced nonlinear detector to improve signal detection in non－Gaussian noise［J］.Signal Processing，2006，86：3456－3465.

［9］Jha R K，Biswas P K，Chatterji B N.Image segmentation using suprathreshold stochastic resonance［J］.World Academy of Science，Engineer and Technology，2010，72：695－709.

［10］Patel A，Kosko B.Noise benefits in quantizer－array correlation detection and watermark decoding［J］.IEEE Transactions on Signal Processing，2011，59（2）：488－505.