薄丝织物弯曲刚度及延伸率与缝缩率的关系

吴巧英，蒋丽君，张文斌

(1.东华大学服装·艺术设计学院，上海200051;2.现代服装设计与技术教育部重点实验室(东华大学)，上海200051;3.浙江理工大学服装学院，杭州310018)

深入了解织物缝纫性能对于合理选料、选款，提高服装产品质量至关重要。服装缝纫对小负荷区域的力学性能很敏感，因此关于织物力学性能对缝纫缩皱影响的研究一直备受关注并已有相关报道。Amirbayat等[1-2]推导出织物缝纫起皱的临界起皱应变条件公式，指出织物弯曲刚度、拉伸模量分别对缝纫缩皱为反向和正向影响。Kawabata等[3]通过力学分析，推导出织物缝纫起皱的临界缝缩率计算公式，指出织物弯曲刚度、轴向压缩系数分别对缝纫缩皱为反向和正向影响。上述缝纫起皱的力学研究为缝纫缩皱实验研究的开展起到了积极的指导作用，由于织物轴向压缩系数难以测量，织物延伸率与拉伸模量、压缩系数关系密切，因此研究中通常采用织物延伸率来替代。在薄型织物力学性能与缝缩率关系研究方面，学者们通常采用相关分析、回归分析探讨两者关系。高雪莲等[4]研究发现，薄丝织物经向延伸率对经向缝缩率为显著正向相关，而纬向延伸率与纬向缝缩率为负相关，不同纱向织物缝缩率受延伸率的影响趋势截然相反。WU Qiaoying[5]建立了薄丝织物弯曲刚度对缝缩率的对数函数模型，并分别用二次、三次曲线模型拟合经向和纬向延伸率与缝缩率关系。常婷[6]建立了经向延伸率对缝缩率的三次曲线模型，亦发现纬向延伸率与缝缩率为低负相关关系，与经向情况相反。但上述研究并未对模型参数的显著性作检验，影响了所建模型的可靠性。

本研究以品质要求高、缝纫缩皱问题较严重的薄丝织物为试验对象，通过回归分析，建立经向弯曲刚度、延伸率对经向缝缩率的回归模型，深入揭示织物力学性能对缝纫缩皱的影响机理，以期为织物性能对缝纫缩皱的预测研究奠定基础，为服装企业快速、合理地选择薄丝织物提供参考。

1 试验

1.1 试 样

选取20种具有代表性的常用薄平纹丝织物作为试验样品，平方米质量小于 86.11g/m2[7]，试样基本覆盖薄丝织物的平方米质量范围，原料包括蚕丝、蚕丝与棉交织、涤纶等，织物规格见表1。

表1 织物基本参数Tab.1 Basic parameters of fabrics

1.2 织物弯曲刚度和延伸率测试

在标准温湿度条件下，采用FAST风格仪测试负荷分别在 4.9、19.8、98.0 N/m 下的经向延伸率 E5、E20、E100(%)，测试织物经向抗弯长度L(mm)，并通过计算得到织物经向弯曲刚度B(μN·m)。

1.3 织物缝纫缩皱测试

选择缝纫皱缩程度最严重的经向丝缕[4]作研究，裁剪20种试样尺寸规格为35 cm×6 cm的经向缝条，相同试样准备3组。为了避免缝纫参数对缝纫缩皱测试结果的影响，采用相同缝纫条件，选用DDL-8500-7兄弟牌电脑缝纫机，平车E型胶牙送布牙、E16针板、塑胶压脚、7号球形机针，线迹密度15针/3 cm，9.8×2 tex涤纶线。由同一名丝绸服装厂熟练技术工按上述缝纫条件进行缝制。

体现织物缝纫前、后尺寸变化特征的缝缩率指标有助于查找服装缝纫起皱问题产生的原因，是缝皱研究中最为常用的评价指标[4-6，8-10]，也被广泛应用于服装生产的质量控制，因此本研究采用缝缩率Ss对各试样缝纫缩皱程度进行客观评定，Ss=(L0－L1)/L0×100%[3]，其中，L0为织物缝前长度;L1为织物缝后长度。

2 结果与分析

2.1 试验结果

织物经向弯曲刚度、延伸率及缝纫缩皱客观评价指标缝缩率的测试结果如表2。

2.2 数据分析

2.2.1 经向延伸率代表性指标的选取

由FAST测试仪得到的3个不同负荷下的延伸率指标间相关系数均为高度正线性相关，其中E5与E20及E100、E20与 E100之间相关系数分别为 0.949、 0.886和0.990，指标间信息重叠程度非常高。

表2 织物经向弯曲刚度、延伸率及缝缩率的测试结果Tab.2 Test results of warp-wise bending rigidity，percentage of elongation and sewing shrink ratio

采用相关指数最大法从3个经向延伸率指标中选取包含信息量最丰富的代表性指标[8]。计算第j个指标对第i个指标的相关指数，其中 rij为相关系数，i≠j，j=1，2，…，m，m 为指标个数。得到 E5、E20及 E100的相关指数分别为0.843、0.925、0.867，由此选择相关指数最大的 E20作为代表性指标。

2.2.2 弯曲刚度与延伸率的关系

织物经向弯曲刚度B与延伸率E20之间的回归分析结果见表3，两者之间的关系见图1。由表3和图1可知，经向弯曲刚度B随着经向延伸率E20的增大先快速递减，减速迅速减小，当B降低至1 uN·m附近，随着E20的继续增大B仅略微减小，两者为倒数曲线函数关系。表3可见，E20对B的倒数曲线模型的决定系数R2为0.934，接近1，表明该模型能很好地解释两者之间的关系。

表3 经向延伸率E20对经向弯曲刚度B的回归分析结果Tab.3 Regression analysis results of warp-wise percentage of elongation E20 to warp-wise bending rigidity B

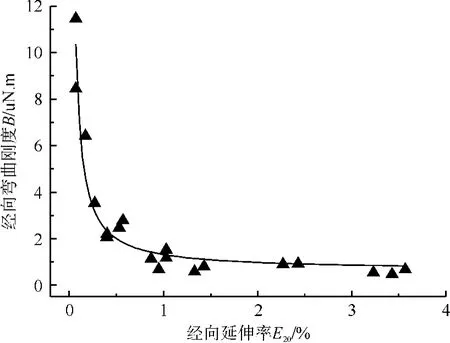
图1 经向延伸率E20与经向弯曲刚度B的关系Fig.1 Relationship between warp-wise percentage of elongation E20 and warp-wise bending rigidity B

2.2.3 弯曲刚度、延伸率与缝缩率的关系

织物经向弯曲刚度B、延伸率E20与经向缝缩率Ss之间的回归分析结果见表4、表5。由表可见所有回归模型及回归系数显著性检验的概率p值均小于显著性水平α(α取0.05)，表明回归模型及回归系数有统计意义，经向弯曲刚度和延伸率对缝缩率有影响显著。比较两个模型的决定系数R2，可见经向弯曲刚度B与缝缩率Ss的关系更紧密，影响更强。

表4 经向弯曲刚度对经向缝缩率的回归分析结果Tab.4 Regression analysis results of warp-wise bending rigidity to warp-wise sewing shrink ratio

表5 经向延伸率对经向缝缩率的回归分析结果Tab.5 Regression analysis results of warp-wise percentage of elongation to warp-wise sewing shrink ratio

由表4和图2可知，在经向弯曲刚度B小于1μN.m左右的较低区域，经向缝缩率Ss随着B的增大呈快速递增趋势，在B大于1μN·m左右的较高区域，Ss随着B的增大先快速递减，而后减速变缓，两者为分段函数关系。由表5和图3可知，经向缝缩率Ss随着经向延伸率E20的增大呈先增后减趋势，两者为二次曲线函数关系。这是由于织物缝纫收缩受弯曲刚度B及延伸率E20的共同影响[1-3]，织物弯曲刚度B增加，织物对缝纫中缝线张力作用而产生缝缩的抵抗力增加，织物缝缩率Ss减小;与此同时，织物延伸率E20随着弯曲刚度B的增加而降低，织物缝纫过程中伸长变形能力降低，使织物产生缝缩的缝线张力增大，从而使织物缝缩率Ss增大。因此，当B的增加对缝缩率Ss的降低作用强于延伸率E20－1的减小对缝缩率Ss的增高作用，则Ss表现为递减趋势，即与B呈反向关系而与E20呈正向关系，反之则趋势相反。如图1所示，对于B较高E20较低区域的织物，B的减速远高于E20的增速，故B对Ss的反向作用更强，表现为随着B减小、E20增加，Ss呈递增趋势;对于B较低E20较高区域的织物，B的减速远低于E20的增速，故随着 B减小、E20增加，Ss呈递减趋势。

图2 经向弯曲刚度B与经向缝缩率Ss的关系Fig.2 Relationship between warp-wise bending rigidity B and sewing shrink ratio Ss

图3 经向延伸率E20与经向缝缩率S s的关系Fig.3 Relationship between warp-wise percentage of elongation E20 and sewing shrink ratio S s

3 结论

1)由FAST测试仪得到的3个不同负荷下的延伸率指标高度相关，其中20 cN负荷下的织物延伸率E20相关系数最高，包含3个指标的信息达92.5%，是最能体现薄丝织物经向延伸率的代表性指标。

2)薄丝织物经向延伸率E20对弯曲刚度B的回归模型为:B=0.63+0.68/E20，决定系数为 0.934，表明两力学性能指标间存在极强的倒数函数关系。

3)织物缝缩率受Ss弯曲刚度B和经向延伸率E20的共同影响，当B的增加对缝缩率Ss的降低作用强于延伸率E20－1的减小对缝缩率Ss的增高作用，则Ss表现为递减趋势，即与B呈反向关系而与E20呈正向关系，反之则趋势相反。

4)分别建立了薄丝织物经向弯曲刚度B、经向延伸率E20对经向缝缩率Ss的分段函数模型和二次曲线函数模型，结果表明，随着织物B及E20的增大，Ss均呈现先增后减的趋势。由此得出，硬挺织物或易拉伸织物不易出现缝皱，柔软而不易拉伸的织物易出现严重缝皱。

[1]AMIRBAYAT J.An energy approach to the instability problem of overfeed seams(part1):the oretical analysis[J].International Journal of Clothing Science and Technology，1990，2(1):21-25.

[2]AMIRBAYAT J，NORTON M L.An energy approach to the instability problem of over feed seams(part 2):experimental analysis[J].International Journal of Clothing Science and Technology，1990，2(2):7-13.

[3]KAWABATA S，NIWA M.Clothing engineering based on objective measurement technology[J].International Journal of Clothing Science and Technology，1998，10(3/4):263-272.

[4]高雪莲，吴巧英，武利利.薄丝织物结构、性能与缝纫缩皱的关系[J].丝绸，2011，48(3):22-25.GAO Xuelian，WU Qiaoying，WU Lili.Research on the relationship between structure，performance and seam puckers of thinsilk fabrics[J].Journal of Silk，2011，48(3):22-25.

[5]WU Qiaoying，ZHANG Wenbin.Influence of mechanical properties of light weight silk fabrics on seam shrinkage[J].Advanced Material Research，2011(1):119-122.

[6]常婷，方丽英，潘婷，等.大豆蛋白纤维机制织物性能对缝缩率的影响[J].浙江理工大学学报，2011，28(5):723-727.CHANG Ting，FANG Liying，PAN Ting，etal.Influence ofsoybean protein woven fabrics characters on garment shrinkage[J].Journal of Zhejiang Sci-Tech University，2011，28(5):723-727.

[7]冯岑.真丝绉类织物洗涤缩水率的测试分析[J].江苏丝绸，2001(5):31-33.FENG Cen.Test analysis ofsilk crepe fabric washingshrinkage[J].Jiangsu Silk，2001(5):31-33.

[8]唐虹.雪纺织物性能与缝缩方向性研究[J].纺织学报，2008，29(10):87-91.TANG Hong.Study on properties ofsilk chiffon and itsseam puckering directions[J].Journal of Textile Research，2008，29(10):87-91.

[9]武利利，吴巧英，冯婉婉.薄型丝织物缝纫缩皱与缝纫线纤度及施加张力的关系[J].丝绸，2012，49(6):31-35.WU Lili， WU Qiaoying， FENG Wanwan. Relationship betweensewing thread fineness and external tension of thin silk fabricseam pucker[J].Journal of Silk，2012，49(6):31-35.

[10]付强，金子敏，周洁雅，等.三角中空锦纶丝无缝针织织物的外观性能研究[J].现代纺织技术，2012(2):10-12.FU Qiang，JIN Zimin，ZHOU Jieya，etal.Astudy on appearance performance of seamless knitting fabric made of riangle-hollow nylon [J].Advanced Textile Technology，2012(2):10-12.

[11]薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社，2007:157-158.XUE Wei.SPSS Statistical Analysis Methods and Applications[M].Beijing:Electronic Industry Press，2007:157-158.