基于三角模糊数—TOPSIS法的随车吊结构形式比选

陈治虎，吕宏庆，刘伦格

（1.后勤工程学院，重庆 401311；2.78421部队，贵州 安顺 561014）

近几年，海军护航、巡逻、演习等多样化军事任务不断增多，岸基油料保障呈现出时间紧、任务重、要求高、专用保障装备缺乏等特点。作为岸基油料保障的重要组成部分，大容量桶装油料还基本依靠人力搬运上舰，效率非常低。随车起重机作为一种集运输和起吊于一体的新兴装卸搬运装备应用范围广、操作简便、军民通用性强，稍加改造即可用于开展桶装油料上舰作业，从而减少人力使用，提高作业效率。随车吊分折叠臂和直臂两种结构形式，因结构和原理不同，两种随车吊主要在工作效率、适用性、功能扩展、操作性、维修性及成本等六个方面存在差异，各有优劣，因此在起重吨位相同的情况下具体选择何种结构形式还有待进一步采用科学评价方法来进行决策。

方案比选受多重指标（因素）影响，实际中由于指标信息的不完全或不精确，使得某些指标及各指标的权重只能用文字来描述，可视为模糊多指标决策问题。在解决模糊决策问题时，通常采用模糊评判法，其评价结果与评价者的知识水平、经验、个人偏好等有关。TOPSIS是进行方案比选时常用的一种科学方法，因此，本文拟采用三角模糊数—TOPSIS法建立随车吊结构形式的比选模型。

1 建立评价指标体系

卢凯等人在《基于模糊综合评判的空军油料节约评估》[1]中对指标和指标体系的内涵进行了阐述，指出指标是反映客体数量特征的一种范畴，具有客观、有效、敏感、特异等特点。对随车吊结构形式进行评价比选，也必须遵循这些特点，按照一定标准进行。通过资料查找、咨询、分析和筛选，最终将指标体系分为二级。随车吊结构形式选择是总目标，为第一层次；作业能力、适用性、操作性、维修性和经济性作为1级指标，即第二层次；将1级指标展开作为2级指标，递阶层次结构见图1。

2 建立比选模型

2.1 几个重要定义及运算规则[2-3]

定义1：具有隶属函数μA且满足以下条件的模糊集合A即可称为模糊数：

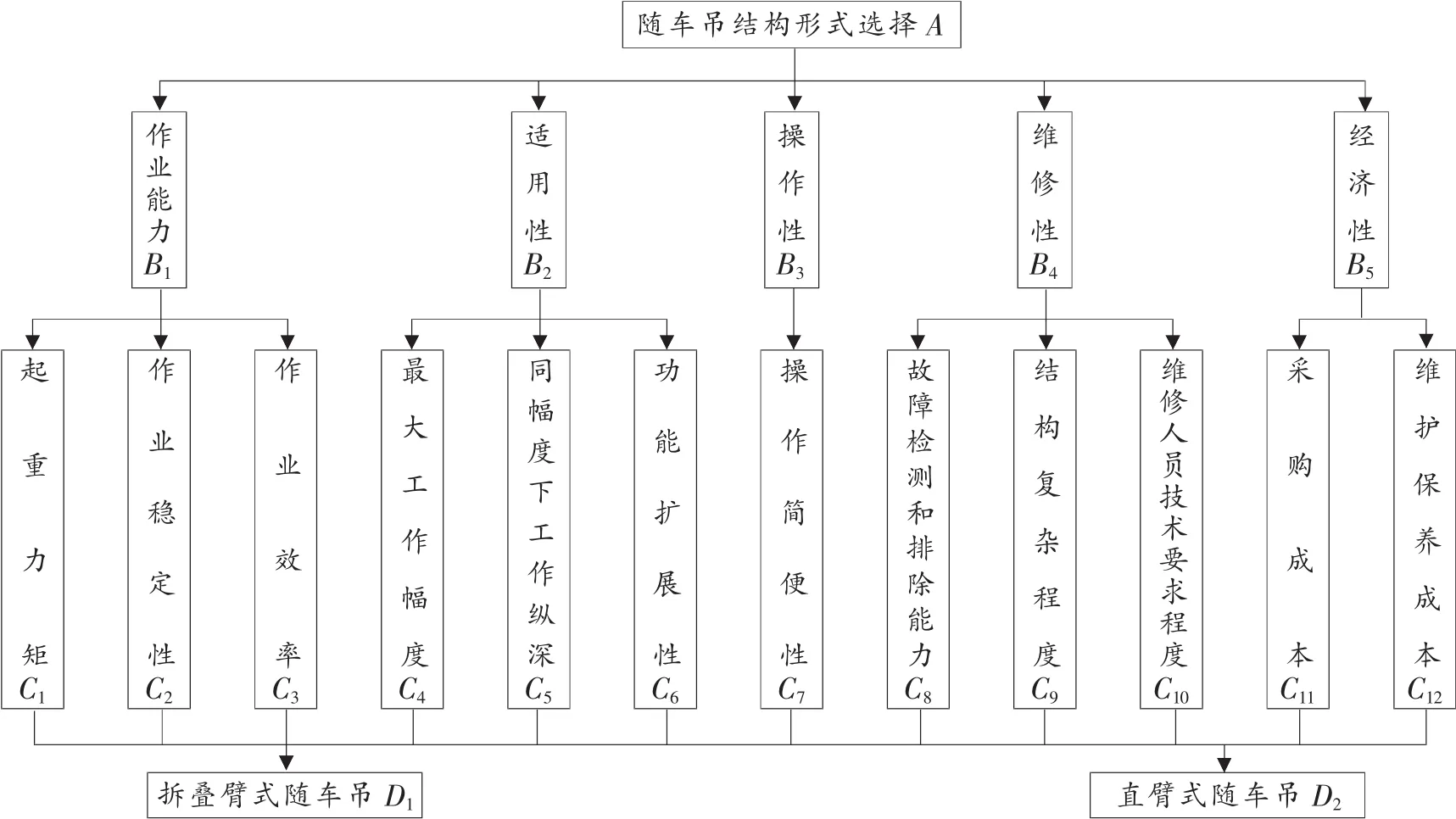
图1 随车吊结构形式评价指标体系

（1）μA是实数R到闭区一个连续映射；

其中，a、b、c均为实数。

定义2：如果一个模糊数的隶属函数给定如下，则称为三角模糊数

其中，a、b、c均为实数。

三角模糊数的运算规则：

2.2 比选模型建立

（1）构建专家决策判断矩阵Rk,k=1,…,K

表1 三角模糊数值表[4]

（2）综合每位专家给出的指标权重和决策判断矩阵

计算k位专家评价结果的综合值。由于实际中每位专家对该领域的熟悉程度不同，在此用ϖk表示第k位专家对该领域的熟悉度（用百分比表示），则k位专家给出的权重值和判断矩阵元素值综合结果分别表示为仍为三角模糊数：

（3）三角模糊数去模糊化及权重向量归一化

三角模糊数去模糊化方法有多种，本模型采用Chen和Hsieh[5]提出的方法将三角模糊数用清晰值表示，假定有模糊数由上式可计算得出专家权重向量和决策判断矩阵相应的清晰值形式：

将由（11）式得到的权重向量归一化：

（4）用TOPSIS法进行比选[6]

TOPSIS法原理在此不再赘述，具体计算步骤如下：

①建立1级指标作业能力B1（）的决策评价矩阵并进行规范化

②构建加权规范矩阵

由步骤（3）得到作业能力（B1）各属性的归一化权重向量则加权规范化矩阵元素值为：

③确定正理想解和负理想解

其中，J*代表效益型指标集，J'代表成本型指标集。

④分别计算与正理想解、负理想解之间的距离

⑤计算与理想解的相对接近度

⑥重复步骤①～⑤，分别计算出其他1级指标的相对贴近度，建立贴近度矩阵

⑧对两种随车吊结构形式的优劣进行排序，根据评价值的大小进行降序排列，可以从中选出相对理想的结构形式。

3 数值计算

限于篇幅，在此不演示具体数值计算过程，据此比选模型计算的结果为即采用直臂式随车吊更好，该结果较符合实际情况。

4 结 论

本文采用基于集体决策环境的三角模糊数—TOPSIS法对两种结构形式随车吊的综合效费进行了评价，三角模糊数可以较好地量化一些模糊不确定的语言描述，将定性指标定量化，模型原理简单，计算结果可信度较高，适于指标不太多的各种方案比选。

[1]卢凯，郭继坤，杨庆.基于模糊综合评判的空军油料节约评估[J].后勤工程学院学报，2010,26(3):51.

[2]王建宏.模糊数学基础[EB/OL].(2006-06-09)[2012-10-08].http://wenku.baidu.com/view/31e4631c59eef8c75fbfb38d.html.

[3]冉静学.三角模糊数排序方法的研究[J].中央民族大学学报，2011,20(4):37-38.

[4]A.Hadi—vencheh,M.N.Mokhtarian.A new fuzzy MCDM approach based on centroid of fuzzy numbers[J].Expert Systems with Application,2011(38):5228.

[5]I.Chamodrakas,N.Alexopoulou,D..Martakos.Customer evaluation for order acceptance using a novel class of fuzzy methods based on TOPSIS[J].Expert Systems with Applications,2009(36):7411.

[6]Metin Dagdeviren,Serkan Yavuz,Nevzat Kilinc.Weapon selection using the AHP and TOPSIS methods under fuzzy environment[J].Expert Systems with Application,2009(36):8145.