基于非球面透镜的光纤耦合系统设计
陈海涛,杨华军,黄小平,程晓洪
(1.宜宾学院物理与电子工程学院,四川省高校计算物理重点实验室四川宜宾644000;2.电子科技大学物理电子学院,四川成都610054)
1 引言
作为一种保密性强且使用灵活的高带宽的通信方式,空间光通信引起人们越来越多的关注[1-5]。有效将激光耦合进单模光纤是自由空间光通信的关键技术。这就需要在光纤耦合系统设计和运行中尽可能提高耦合效率和获得理想的信噪比。但是,由于存在着许多因素影响到光纤耦合的耦合效率[2,5]。因此,将激光耦合进单模光纤最大的挑战就是如何优化设计耦合系统从而有效提高耦合效率。
本文首先对空间光通信中耦合系统耦合效率进行了讨论,然后设计了非球面透镜作为系统的耦合透镜,并采用精密光纤支架对耦合光纤进行准确定位使耦合光聚焦在光纤端面上。最后对所设计的光纤耦合系统的效率进行了实验测量和讨论。
2 光纤耦合系统的耦合效率
空间光通信中所用的光纤耦合器原理如图1所示。平行光束经过焦距为f的薄透镜A聚焦在接收孔径平面上A点。单模光纤端面位于透镜焦平面xOy上。

图1激光到单模光纤耦合器
光纤耦合器的耦合效率定义为有效耦合进单模光纤的光功率Pc与到达接收孔径平面的光功率Pa之比,即:

根据Parseval-Plancherel原理,该耦合效率也可以表示为[6-7]:
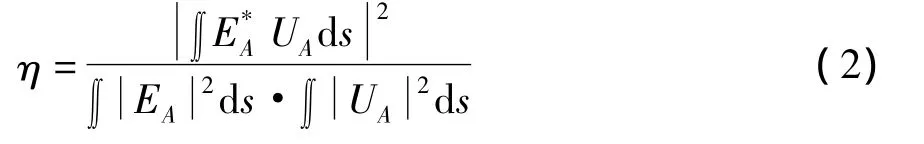
其中,EA接收孔径平面的入射光场;UA是传播到接收孔径平面的光纤本征模。在平面波入射情形下,式(2)可以写为[7]:

其中,β=πRrw0/(λf)为耦合参数;Rr是接受孔径的半径;w0为单模激光的光腰半径;λ为光波长。由式(3)可见:耦合效率先是随着β的增大而增大,并在β=1.1209时达到最大值81.45%;随后,随着β的增大,耦合效率反而减小。
3 消球差非球面透镜设计
虽然光纤耦合系统的耦合效率理论上可以达到81.45%,但是实际上由于许多因素的影响,导致耦合效率很低。其中,耦合透镜的球差对耦合效率的影响不容忽视。透镜球差是光束入射在一般透镜上产生的一种光效应,表现为离主光轴不同距离的平行光轴的光线,并不能严格汇聚于光轴上同一点。不过,球差的大小跟透镜的形状有关。因此,可选用非球面透镜并进行优化设计从而使球差达到最小,以此来改进聚焦光斑的质量,达到改进耦合效率的目的。
非球面透镜如图2(a)所示,透镜的一个表面为非球面另一个表面为平面,n1是透镜材料的折射率。主光轴上一个点光源O发出球面光束,照射到透镜的前表面并发生折射,其中θ和θ'分别代表入射角和折射角。假定通过球面上任一点(x,y)的光线的光程都相等,等于旁轴光线的光程,即:
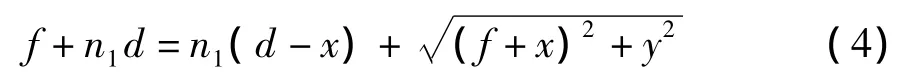
对式(4)进行整理得:

这就是消球差非球面透镜的数学表达式。对于实际透镜材料,选取折射率n1=1.517,透镜的焦距取作f=15.29 mm。在此情形下,非球面透镜方程(5)可以表示为:
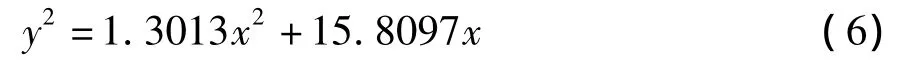
从公式(6)和图2(b)可以看出,所设计的消球差透镜为平凸透镜,它的通光孔径为5.30 cm,透镜的外径为6.50 cm,透镜的中央厚度为2.20 cm。

图2 非球面消球差透镜原理图
4 光纤耦合器的组成及实验测试
要使通过透镜的光束准确聚焦在光纤端面上,还需要考虑光纤的横向偏移、轴向偏移和端面偏转对耦合效率的影响[8]。为了有效减小光纤端面偏移或者偏转的影响,采用四维精密光纤支架,不仅可以实现对光纤端面进行准确固定,还可以在系统实验或者运行过程中,通过一边观察光功率计或者CCD显示器,一边对光纤位置进行四维微调,以取得最佳的耦合效果。设计制作的光纤耦合器如图3(a)所示,单模光纤直径采用纤芯直径9μm。由于光纤直径比较小,尝试环境的细微变化可能会显著影响实验结果,因此对耦合的测试环境要求比较高。尽可能保持实验环境的温度不变,并且将光学系统安装在防震动光学平台上(如图3(b)所示),避免由于震动而造成聚焦光束不能准确耦合到光纤端面上。

图3 光纤耦合器和耦合实验装置
虽然同一个透镜对于不同波长的激光的折射率不同,例如使用透镜材料对于波长1550 nm和632.8 nm光 的 折 射 率 分 别 为 1.500223 和1.514664,这会导致光束焦点偏移23μm。根据耦合效率公式[8]:

由于光波长不同,引起的耦合效率的波动非常小以致可以忽略不计。虽然光通信常采用波长1550 nm的激光,但该频率的光为不可见光,给测试工作带来困难。因此,实验测试采用波长的可见光进行。两个光功率计分别测试耦合的入射光功率和出射光功率。实验结果如表1所示。由此可见,耦合系统的耦合效率大约为60%。

表1 光纤耦合系统耦合效率测试数据表
5 结论
为了提高空间光耦合到单模光纤的耦合效率,我们设计了非球面耦合透镜来降低耦合损失,并采用了精密光纤支架对光纤端面进行准确定位。实验测试显示系统的耦合效率达到η=60%。本研究结果有助于改进空间光通信的耦合效率,提高空间光通信质量。
[1] D Song,Y Hurh,JCho,et al.410 Gb's terrestrial optical free space transmission over 1.2 km using an EDFA preamplifier with 100 GHz channel spacing[J].Opt Express,2000,7:280 -284.
[2] M Toyoshima.Maximum fiber coupling efficiency and optimum beam size in the presence of random angular jitter for free-space laser systems and their applications[J].Opt Soc Am A,2006,23:2246 -2250.
[3] A Polishuk,SArnon.Optimization of a laser satellite communication system with an optical preamplifier[J].Opt Soc Am A,2004,21:1307 -1315.
[4] M Traub,H D Pluma,H D Hoffmanna,et al.Spaceborne fiber coupled diode laser pump modules for intersatellite communications[J].Proc SPIE,2007,6736:673618.
[5] JMa,F Zhao,L Tan,et al.Plane wave coupling into single-mode fiber in the presence of random angular jitter[J].Appl Opt,2009,27:5184 -5189.
[6] P JWinzer,W R Leeb.Fiber coupling efficiency for random light and its applications to lidar [J].Opt Lett,1998,23:986 -988.
[7] OWallner,P JWinzer,W R Leeb.Alignment tolerances for plane-wave to single-mode fiber coupling and their mitigation by use of pigtailed collimators[J].Appl Opt,2002,41:637 -643.
[8] Haitao Chen,Huajun Yang,Tuohui Li,et al.Influence of the fiber displacement on coupling lightbeam into single mode fiber[J].Laser & Infrared,2011,41(1):75 -78.(in Chinese)
陈海涛,杨华军,李拓辉,等.光纤偏移对空间光-单模光纤耦合效率的影响[J].激光与红外,2011,41(1):75-78.

